Análise de componentes principais para mapas perceptivos (toothpaste dataset)
Neste capítulo, você aprenderá como realizar uma análise de componentes principais e visualizar os resultados em um mapa perceptivo.
Digamos que tenhamos um conjunto de observações que diferem entre si em várias dimensões; por exemplo, temos várias marcas de uísque (observações) classificadas em vários atributos, como corpo, doçura, sabor, etc. (dimensões ) Se algumas dessas dimensões estiverem fortemente correlacionadas, deve ser possível descrever as observações por um número menor (que o original) de dimensões sem perder muita informação. Por exemplo, doçura e frutificação podem ser altamente correlacionadas e, portanto, podem ser substituídas por uma variável. Essa redução de dimensionalidade é o objetivo da análise de componentes principais.
Dados
Importação
Analisaremos os dados de uma pesquisa na qual 60 consumidores foram convidados a responder a seis perguntas sobre pasta de dente. Esses dados foram coletados pelos criadores do Radiant}, que é um pacote do R para análise de negócios que usaremos posteriormente. Faça o download dos dados aqui e importe-os para o R:
## -- Attaching packages -------------------------------------------------- tidyverse 1.3.0 --## v ggplot2 3.3.2 v purrr 0.3.4
## v tibble 3.0.3 v dplyr 1.0.0
## v tidyr 1.1.2 v stringr 1.4.0
## v readr 1.3.1 v forcats 0.5.0## -- Conflicts ----------------------------------------------------- tidyverse_conflicts() --
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()library(readxl)
url<-"http://users.telenet.be/samuelfranssens/tutorial_data/toothpaste.xlsx"
toothpaste <- tempfile()
download.file(url, toothpaste, mode="wb")
toothpaste<-read_excel(path = toothpaste, sheet = 1)
toothpaste## # A tibble: 60 x 9
## consumer prevents_caviti~ shiny_teeth strengthens_gums freshens_breath
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 7 3 6 4
## 2 2 1 3 2 4
## 3 3 6 2 7 4
## 4 4 4 5 4 6
## 5 5 1 2 2 3
## 6 6 6 3 6 4
## 7 7 5 3 6 3
## 8 8 6 4 7 4
## 9 9 3 4 2 3
## 10 10 2 6 2 6
## # ... with 50 more rows, and 4 more variables:
## # decay_prevention_unimportant <dbl>, attractive_teeth <dbl>, age <dbl>,
## # gender <chr>Manipulação
## # A tibble: 60 x 9
## consumer prevents_caviti~ shiny_teeth strengthens_gums freshens_breath
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 7 3 6 4
## 2 2 1 3 2 4
## 3 3 6 2 7 4
## 4 4 4 5 4 6
## 5 5 1 2 2 3
## 6 6 6 3 6 4
## 7 7 5 3 6 3
## 8 8 6 4 7 4
## 9 9 3 4 2 3
## 10 10 2 6 2 6
## # ... with 50 more rows, and 4 more variables:
## # decay_prevention_unimportant <dbl>, attractive_teeth <dbl>, age <dbl>,
## # gender <chr>O conjunto de dados consiste em um identificador, consumer}, e as classificações do entrevistado sobre a importância de seis atributos de pasta de dente: prevents_cavities, shiny_teeth, strengthens_gums, freshens_breath, decay_prevention_unimportant, and attractive_teeth. Nos também temos os respondentes age e gender.
Vamos fatorar o identificador e o gender :
Recapitulação: importação e manipulação
Aqui está o que fizemos até agora, em uma sequência ordenada de operações canalizadas (faça o download dos dados aqui :
Quantos fatores devemos considerar ?
O objetivo da análise de componentes principais é reduzir o número de dimensões que descrevem nossos dados, sem perder muitas informações. O primeiro passo na análise de componentes principais é decidir o número de componentes ou fatores principais que queremos manter. Para nos ajudar a decidir, usaremos a função pre_factor do pacote radiant:
## Loading required package: radiant.data## Loading required package: magrittr##
## Attaching package: 'magrittr'## The following object is masked from 'package:purrr':
##
## set_names## The following object is masked from 'package:tidyr':
##
## extract## Loading required package: lubridate##
## Attaching package: 'lubridate'## The following objects are masked from 'package:base':
##
## date, intersect, setdiff, union##
## Attaching package: 'radiant.data'## The following objects are masked from 'package:lubridate':
##
## month, wday## The following object is masked from 'package:forcats':
##
## as_factor## The following objects are masked from 'package:purrr':
##
## is_double, is_empty, is_numeric## The following object is masked from 'package:ggplot2':
##
## diamonds## The following object is masked from 'package:base':
##
## date## Loading required package: radiant.design## Loading required package: mvtnorm## Loading required package: radiant.basics## Loading required package: radiant.model## Loading required package: radiant.multivariate##
## Attaching package: 'radiant.multivariate'## The following object is masked _by_ '.GlobalEnv':
##
## toothpaste# armazene os nomes das dimensoes em um vetor para que nao tenhamos que digita-las repetidamente
dimensions <- c("prevents_cavities", "shiny_teeth", "strengthens_gums", "freshens_breath", "decay_prevention_unimportant", "attractive_teeth")
# dica: tambem poderiamos fazer o seguinte:
# dimensions <- toothpaste %>% select(-consumer, -gender, -age) %>% names()
summary(pre_factor(toothpaste, vars = dimensions))## Pre-factor analysis diagnostics
## Data : toothpaste
## Variables : prevents_cavities, shiny_teeth, strengthens_gums, freshens_breath, decay_prevention_unimportant, attractive_teeth
## Observations: 60
## Correlation : Pearson
##
## Bartlett test
## Null hyp. : variables are not correlated
## Alt. hyp. : variables are correlated
## Chi-square: 238.93 df(15), p.value < .001
##
## KMO test: 0.66
##
## Variable collinearity:
## Rsq KMO
## prevents_cavities 0.86 0.62
## shiny_teeth 0.48 0.70
## strengthens_gums 0.81 0.68
## freshens_breath 0.54 0.64
## decay_prevention_unimportant 0.76 0.77
## attractive_teeth 0.59 0.56
##
## Fit measures:
## Eigenvalues Variance % Cumulative %
## PC1 2.73 0.46 0.46
## PC2 2.22 0.37 0.82
## PC3 0.44 0.07 0.90
## PC4 0.34 0.06 0.96
## PC5 0.18 0.03 0.99
## PC6 0.09 0.01 1.00Nas Fit measures, vemos que dois componentes explicam 82% da variação nas classificações. Isso já é bastante e sugere que podemos reduzir com segurança o número de dimensões para dois componentes. Uma regra prática aqui é que a variação cumulativa explicada pelos componentes deve ser de pelo menos 70%.
Análise de Componentes Principais
Vamos extrair somente dois componentes ou fatores:
## Factor analysis
## Data : toothpaste
## Variables : prevents_cavities, shiny_teeth, strengthens_gums, freshens_breath, decay_prevention_unimportant, attractive_teeth
## Factors : 2
## Method : PCA
## Rotation : varimax
## Observations: 60
## Correlation : Pearson
##
## Factor loadings:
## RC1 RC2
## prevents_cavities 0.96 -0.03
## shiny_teeth -0.05 0.85
## strengthens_gums 0.93 -0.15
## freshens_breath -0.09 0.85
## decay_prevention_unimportant -0.93 -0.08
## attractive_teeth 0.09 0.88
##
## Fit measures:
## RC1 RC2
## Eigenvalues 2.69 2.26
## Variance % 0.45 0.38
## Cumulative % 0.45 0.82
##
## Attribute communalities:
## prevents_cavities 92.59%
## shiny_teeth 72.27%
## strengthens_gums 89.36%
## freshens_breath 73.91%
## decay_prevention_unimportant 87.78%
## attractive_teeth 79.01%
##
## Factor scores (max 10 shown):
## RC1 RC2
## 1.15 -0.30
## -1.17 -0.34
## 1.29 -0.86
## 0.29 1.11
## -1.43 -1.49
## 0.97 -0.31
## 0.39 -0.94
## 1.33 -0.03
## -1.02 -0.64
## -1.31 1.56Cargas fatoriais
Veja a tabela abaixo do Factor loadings. Essas cargas são as correlações entre as dimensões originais (prevents_cavities, shiny_teeth, etc.) e os dois fatores que são retidos (RC1 e RC2). Nós vemos que prevents_cavities, strengthens_gums, e decay_prevention_unimportant pontuação alta no primeiro fator, enquanto shiny_teeth, strengthens_gums, e freshens_breath pontuação alta no segundo fator. Poderíamos, portanto, dizer que o primeiro fator descreve preocupações relacionadas à saúde e que o segundo fator descreve preocupações relacionadas à aparência.
Também queremos saber quanto cada uma das seis dimensões é explicada pelos fatores extraídos. Para isso, podemos observar a comunalidade das dimensões (cabeçalho: Attribute communalities). A comunalidade de uma variável é a porcentagem da variação dessa variável que é explicada pelos fatores. Seu complemento é chamado de exclusividade (= 1-comunalidade). A exclusividade pode ser puro erro de medição ou pode representar algo que é medido de forma confiável por essa variável específica, mas não por nenhuma das outras variáveis. Quanto maior a exclusividade, maior a probabilidade de que seja mais do que apenas erro de medição. Uma exclusividade superior a 0,6 é geralmente considerada alta. Se a exclusividade for alta, a variável não será bem explicada pelos fatores. Vemos que, para todas as dimensões, a comunalidade é alta e, portanto, a singularidade é baixa; portanto, todas as dimensões são bem capturadas pelos fatores extraídos.
Gráfico das cargas fatoriais
Também podemos traçar as cargas. Para isso, usaremos dois pacotes:
#install.packages("FactoMiner")
#install.packages("factoextra")
library(FactoMineR)
library(factoextra)## Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBatoothpaste %>% # take dataset
select(-consumer,-age,-gender) %>% # somente duas dimensoes
as.data.frame() %>% # converter em um objeto data.frame, caso contrário, o PCA não o aceitará
PCA(ncp = 2, graph = FALSE) %>% # faça uma análise de componentes principais e retenha 2 fatores
fviz_pca_var(repel = TRUE) # pegue essa análise e a transforme em uma visualização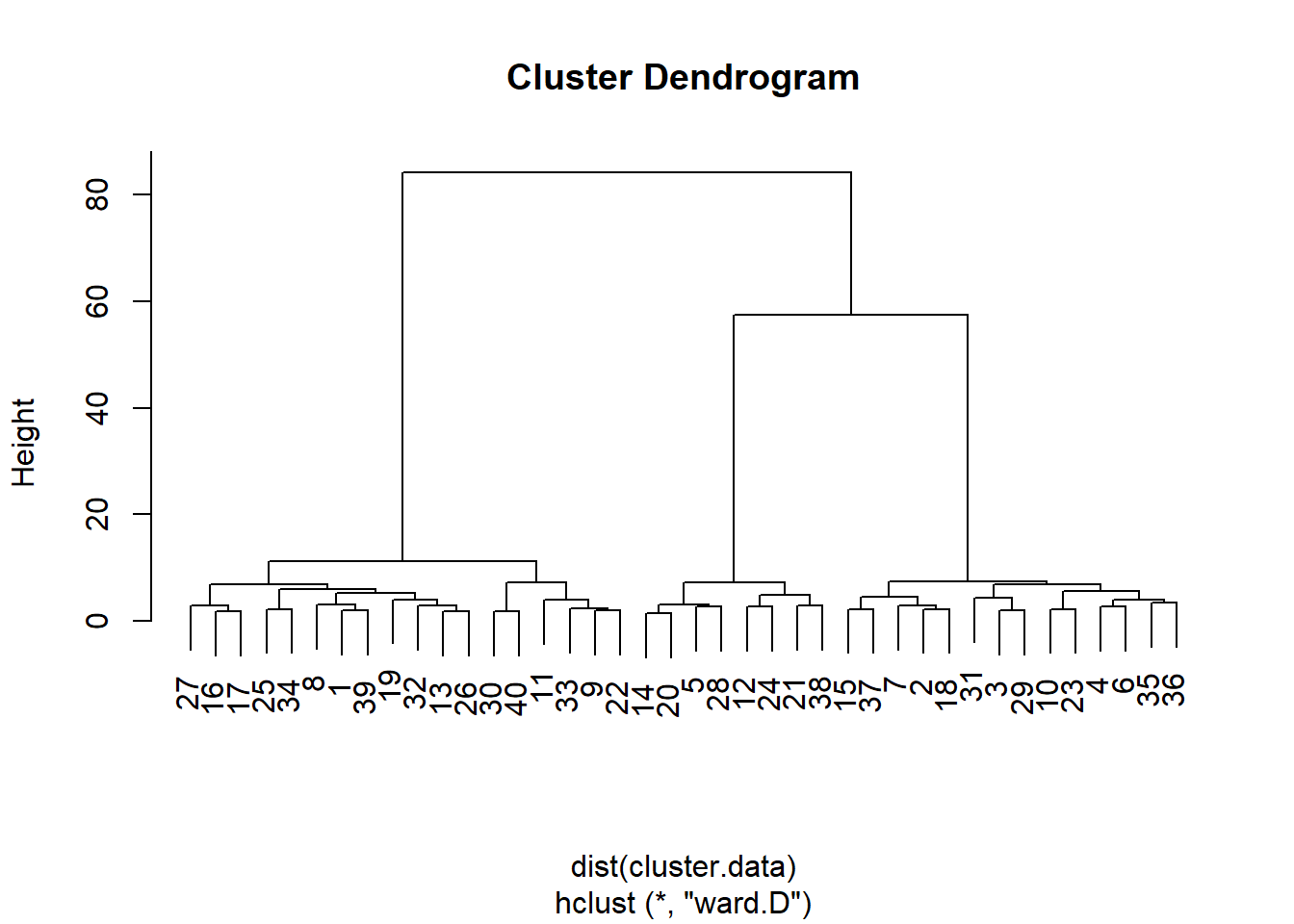
Vemos que attractive_teeth, shiny_teeth, freshens_breath, têm pontuações altas no segundo fator (o Dim2 do eixo X). prevents_cavities e strengthens_gums têm pontuações altas no segundo fator (o eixo Y Dim2) e decay_prevention_unimportant tem uma pontuação baixa nesse fator (essa variável mede a importância da prevenção da cárie).
Também podemos adicionar as observações (os diferentes consumidores) a esse gráfico:
toothpaste %>% # pega os dados
select(-consumer,-age,-gender) %>% # obtem as dimensoes somente
as.data.frame() %>% # converte em data.frame object, caso contratio PCA nao aceita
PCA(ncp = 2, graph = FALSE) %>% # faz o pca e retem 2 fatores
fviz_pca_biplot(repel = TRUE) #faz o grafico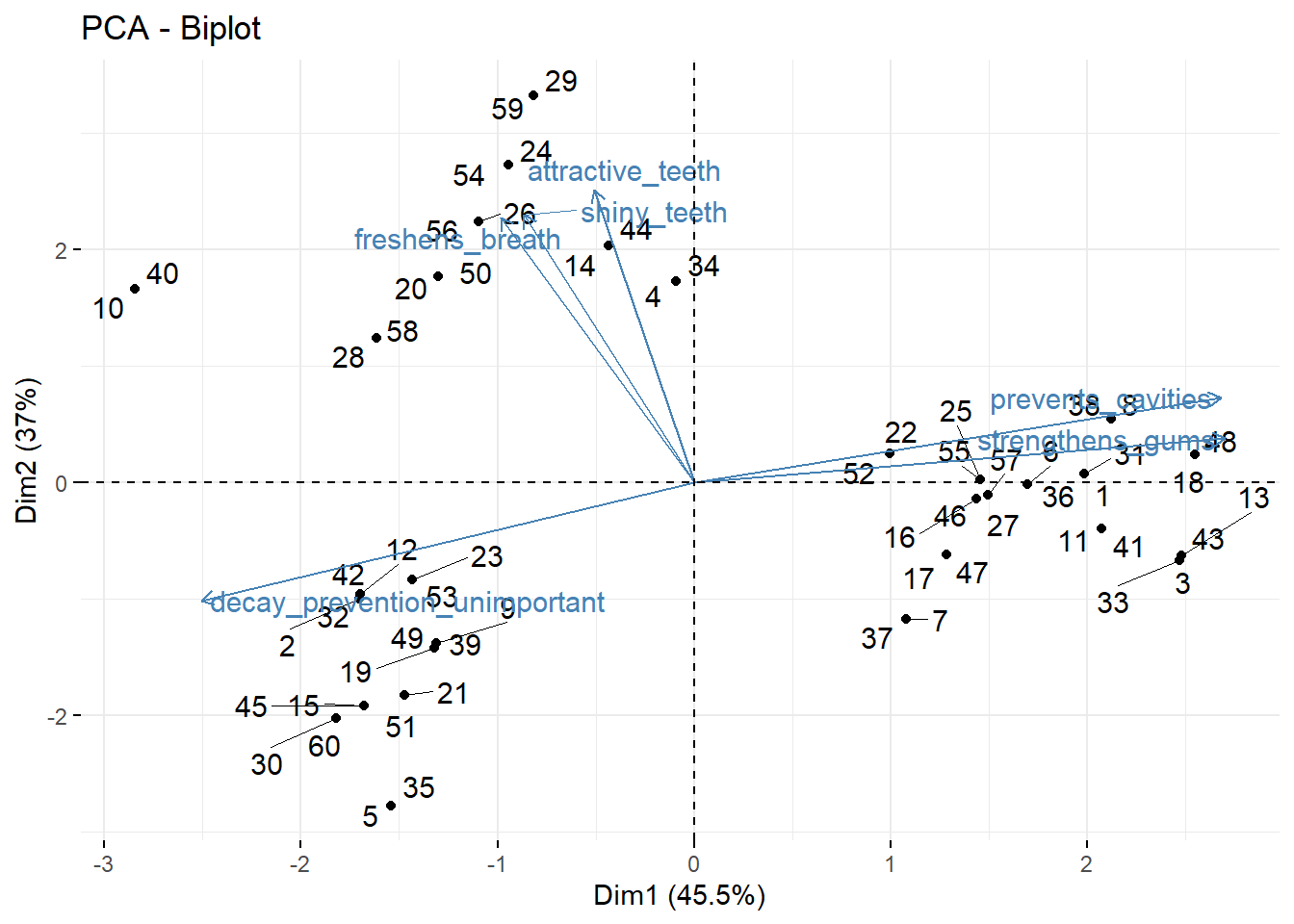
Isto também é conhecido como biplot.