Algoritmos Genéticos para seleção de modelos de regressão
Modelos Econométricos
Conteúdo
…em até 20 minutinhos, pretendo abordar brevemente
Fator de Impacto/Relevância da publicação selecionada
Contextualização do paper recomendado (Hasheminia e Niaki (2006))
Relevância científica e contribuição da pesquisa
Proposta dos autores do paper
Algumas aplicações de código no R da problemática relacionadas ao paper
Esclarecimento de dúvidas
Meus Contatos
Qualis do journal da publicação
- Para o artigo de (Hasheminia e Niaki (2006)) temos a referência completa:
- \(\Rightarrow\) Hasheminia, H., & Akhavan Niaki, S. T. (2006). A genetic algorithm approach to find the best regression/econometric model among the candidates. Applied Mathematics and Computation, 183(1), 337–349. doi:10.1016/j.amc.2006.05.072
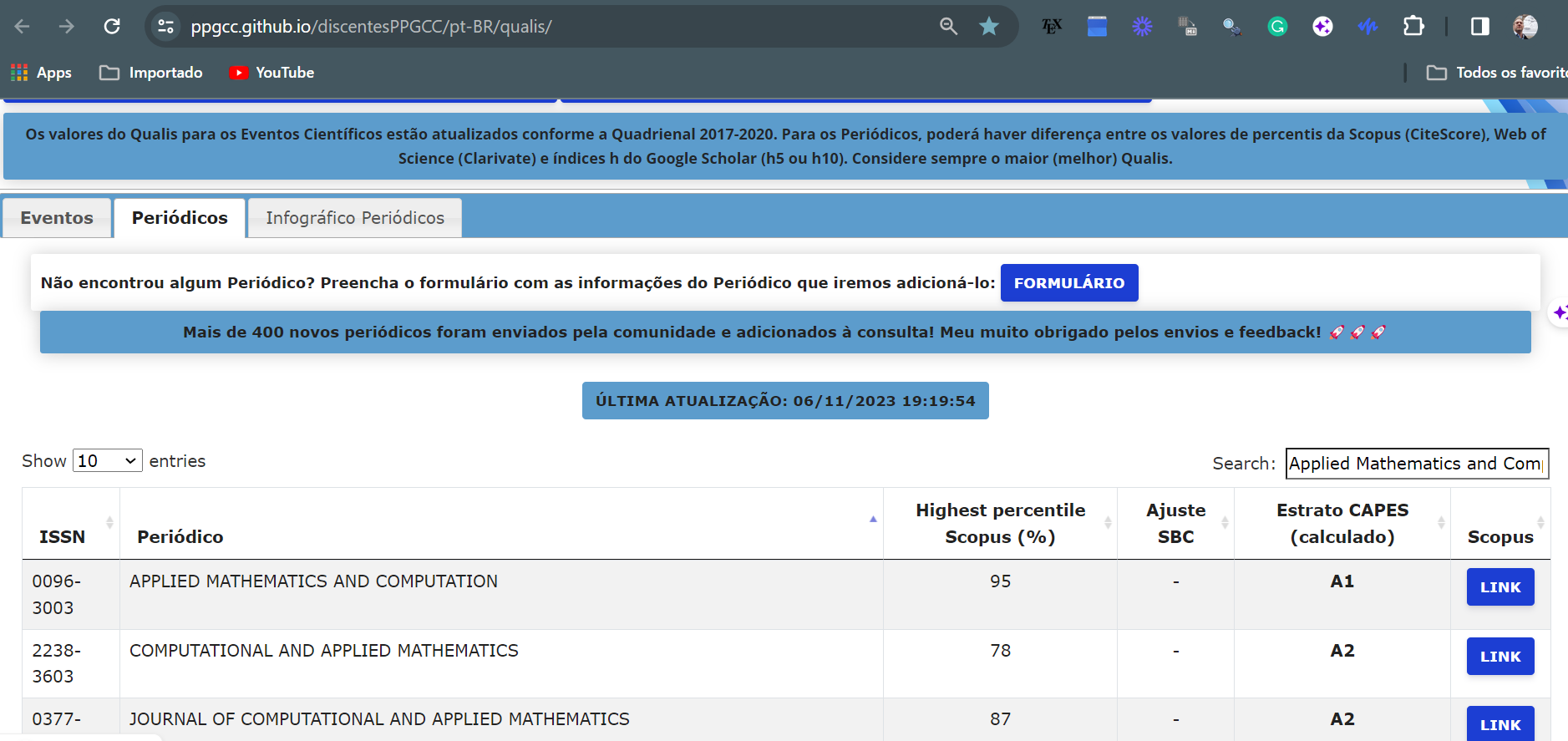
- A checagem do Qualis conforme a categorização nacional pode ser feita em Sistema Sucupira (Engenharias) e para uma busca específica na Ciência da Computação em https://ppgcc.github.io/discentesPPGCC/pt-BR/qualis/
- Como podemos ver ela está classificada no Qualis A1
Contextualização
Contexto e Desafio: A modelagem estatística é amplamente utilizada em várias áreas da ciência, mas encontrar o modelo mais adequado para descrever dados históricos ou experimentais é um desafio.
Classificação das Técnicas de Estimação: As técnicas de estimação são vistas como formas de otimização, o que permite abordar a seleção do modelo estatístico como um problema de otimização.
Solução Proposta: O artigo apresenta um novo tipo de algoritmo genético desenvolvido para identificar o melhor modelo de regressão entre um conjunto de modelos candidatos.
Metodologia: O desempenho do algoritmo genético proposto é avaliado por meio de um estudo de caso no campo da economia.
Contribuição: O trabalho contribui para o campo da pesquisa operacional e técnicas de busca, aplicando uma abordagem transformacional para a seleção de modelos de regressão/econométricos.
Validação: O estudo inclui uma validação prática do algoritmo proposto, destacando sua utilidade e eficácia em um contexto aplicado.
Relevância da Pesquisa
Otimização na Natureza e Ciência: Os autores destacam que, enquanto a natureza tem utilizado métodos de otimização por milhões de anos, os seres humanos começaram a explorar essas técnicas há menos de um século. Eles ressaltam a importância de aprender com estratégias naturais para resolver problemas complexos de otimização combinatória.
Desafios da Otimização Combinatória: Os autores explicam que problemas de otimização combinatória são facilmente modeláveis, mas difíceis de resolver. Devido à sua complexidade e ao tempo necessário para solucioná-los, os autores enfatizam a necessidade de algoritmos heurísticos para encontrar soluções aproximadas.
Aplicação de Algoritmos Heurísticos: Os autores discutem como diversos métodos heurísticos, como recozimento simulado, aceitação por limiar, busca tabu, algoritmos genéticos, redes neurais e otimização de colônia de formigas, têm sido aplicados com sucesso em várias disciplinas para resolver problemas complicados.
Contribuição do Estudo: Os autores propõem um novo enfoque utilizando um algoritmo genético para o problema de ajuste de função em dados disponíveis ou experimentais, abordando este desafio como um problema de otimização. Eles indicam que o estudo contribui para a área ao oferecer uma nova perspectiva e solução para um problema clássico.
Integrando Algoritmos Genéticos com Modelos de Regressão
Aqui enfatizamos a metodologia, seções 2 e 3…
Algoritmos Genéticos: Inspirados na natureza, esses algoritmos buscam a solução ótima (o “vencedor” do jogo genético) através de um processo que imita a evolução biológica, operando em uma população de soluções e utilizando mecanismos de crossover e mutação.
Modelos de Regressão: Ferramentas essenciais em várias áreas para modelar relações estatísticas entre variáveis. Podem ser simples ou múltiplos, lineares ou não lineares, com a escolha da forma funcional das variáveis independentes sendo um desafio significativo.
Otimização de Modelos de Regressão: Os algoritmos genéticos oferecem uma abordagem inovadora para selecionar a melhor combinação de variáveis independentes em modelos de regressão múltipla, superando os desafios de formas funcionais complexas e estimativa de parâmetros.
Processo Evolutivo Aplicado: Utilizando a estrutura dos algoritmos genéticos, é possível explorar eficientemente diversas combinações de variáveis e suas formas funcionais, evoluindo para um modelo que melhor se ajusta aos dados.
Sinergia entre Métodos: A combinação de algoritmos genéticos com modelos de regressão ilustra um exemplo prático de como técnicas de otimização baseadas na natureza podem ser aplicadas para resolver problemas complexos em estatística e econometria.
Otimização de Modelos de Regressão: Integração de Programação Matemática e Algoritmo Genético
- Modelo de Programação Matemática (Seção 4):
- Formulação de um modelo para encontrar a melhor combinação de funções das variáveis independentes em um modelo de regressão linear múltipla.
- Objetivo de minimizar o erro quadrático somado (SSE) ou maximizar o coeficiente de determinação múltipla (R²).
- Desafio de complexidade devido à natureza não linear e variáveis binárias.
- Otimização com Algoritmo Genético (Seção 5):
- Aplicação de mutações e cruzamentos para explorar novas combinações de variáveis e estados.
- Seleção de modelos com menor SSE ou maior R², melhorando a eficiência em comparação com a abordagem de enumeração completa.
- Uso de dominância incompleta/co-dominância para explorar combinações mais complexas de características dos modelos.
- Integração das Abordagens:
- O algoritmo genético oferece uma solução prática para o desafio de complexidade do modelo de programação matemática.
- Permite a exploração eficiente do espaço de soluções, encontrando modelos ótimos com menos esforço computacional.
- Combinação das técnicas aumenta significativamente a capacidade de identificar o modelo de regressão mais adequado para um conjunto de dados.
- Conclusão:
- Esta abordagem integrada representa um avanço significativo na otimização de modelos de regressão, combinando rigor matemático com eficiência computacional.
Avaliação do Algoritmo Genético Proposto
- Comparação de Desempenho (Seção 6):
- Comparação entre o novo algoritmo genético e o método da Seção 4.
- Utilização de 16 observações com cinco variáveis independentes.
- Métodos de Avaliação:
- Dois estágios de mutações e dois de cruzamentos no algoritmo genético.
- Registro do tempo computacional e do Erro Quadrático Somado (SSE) para cada algoritmo.
- Resultados Principais:
- Os valores de SSE são similares entre os dois métodos.
- O algoritmo genético alcança a solução ótima (ou quase ótima) de forma mais eficiente.
- O tempo computacional do algoritmo genético aumenta linearmente com o número de variáveis e estados, enquanto no método simples aumenta exponencialmente.
- Conclusão:
- O algoritmo genético proposto é mais eficaz em termos de tempo computacional, especialmente para problemas com um grande número de variáveis e estados.
- Esta eficiência torna o algoritmo genético uma ferramenta valiosa para otimização em modelos de regressão complexos.
Estudo de Caso: Demanda de Empréstimos em um Banco Iraniano (seção 7)
- Objetivo: Análise de fatores que influenciam a demanda por empréstimos.
- Metodologia: Uso de modelos econométricos com algoritmo genético para previsão e compreensão das tendências de empréstimos.
Variáveis do Modelo:
NGDP: Produto Interno Bruto líquido
NCAP: Capital líquido do banco
ADV: Variável binária de publicidade (0 = Não, 1 = Sim)
EC: Variável binária de crise econômica (0 = Não, 1 = Sim)
UR: Taxa de desemprego
INT: Taxa de juros dos empréstimos financeiros
INF: Inflação
NTA: Montante total de empréstimos solicitados
TN: Número total de pedidos de empréstimos
Independentes (X´s): \(\Rightarrow\) NGDP, NCAP, ADV, EC, UR, INT, INF.
Dependentes (Y): \(\Rightarrow\) NTA (Montante Total de Empréstimos), TN (Número Total de Empréstimos).
Estudo de Caso: Demanda de Empréstimos em um Banco Iraniano (seção 7)
Resultados Principais:
Modelagem Econômica para o Montante Total de Empréstimos (NTA): O algoritmo não encontrou um modelo satisfatório que incluísse todas as seis variáveis independentes. Após várias iterações, um modelo com quatro variáveis independentes (NGDP, UR, ADV, INT) foi aceito.
- Equação: \(NTA = 429.54 + 9.03NGDP - 2.834*UR^2 + 230.78ADV - 1.96INT^2\)
- R² = 0.78, SSE = 136234.9.
- Comparação de Valores Observados e Estimados: Os autores apresentaram gráficos comparando os valores observados e estimados para NTA e TN ao longo de diferentes anos, demonstrando a eficácia do modelo.
- *ver figura 6 do paper
Modelagem Econômica para o Número Total de Pedidos de Empréstimos (TN): Da mesma forma, o melhor modelo para TN incluiu quatro variáveis independentes (NCAP, ADV, EC, UR, e INT).
- Equação: \(NA = 79.34\sqrt{NCAP} + 931.02ADV - 895.65EC + 4.26UR^2 - 85.2INT\)
- R² = 0.90, SSE = 455612.3.
- *ver figura 7
Conclusão dos autores
Novo Algoritmo Genético para Modelos de Regressão
- Objetivo: Desenvolver um algoritmo genético para encontrar o melhor modelo de regressão.
Características do Algoritmo Proposto
- Semelhanças com Algoritmos Genéticos Típicos:
- Possui estágios de mutação e crossover.
- Diferenças Distintas:
- Introduz um novo estágio chamado “formas genéticas de estados de dominância incompleta/co-dominância”.
- Utiliza mutações e crossovers para variáveis independentes e seus diferentes estados, ao contrário dos números binários em algoritmos genéticos típicos.
Implicações e Aplicações
- Flexibilidade: Permite a análise de variáveis independentes em diferentes formas funcionais.
- Aplicabilidade: Demonstrado eficaz em um estudo de caso real, modelando a demanda de empréstimos em um banco em desenvolvimento.
Conclusão
O algoritmo proposto oferece uma abordagem inovadora e eficaz para a seleção de variáveis e construção de modelos de regressão, expandindo as possibilidades de análise em diversos campos.
Os autores não mencionam limitações ou propostas de trabalhos futuros na conclusão do artigo.
Exemplos de aplicação para problema similar em econometria
Neste slide insiro aqui um exemplo que apliquei em R utilizando o pacote glmulti comparando o desempenho de seleção de modelos de regressão em pelo menos dois datasets distintos avaliando a abordagem da força bruta x algoritmo genético.
- Acesse o case de aplicação visitando ☞ rhozon.github.io
Referências
Hasheminia, H., & Akhavan Niaki, S. T. (2006). A genetic algorithm approach to find the best regression/econometric model among the candidates. Applied Mathematics and Computation, 183(1), 337–349. doi:10.1016/j.amc.2006.05.072
Obrigado!
Rodrigo Hermont Ozon
\(\Rightarrow\) Ao professor Erick Oliveira Rodrigues pela oportunidade de contribuir com os novos pesquisadores;
\(\Rightarrow\) Agradecimentos aos pesquisadores do PPGEPS/PUCPR, aos ouvintes e em especial ao meu orientador, prof. Dr. Gilberto Reynoso Meza
- Meu perfil no Google Scholar
- Meu CV Lattes
- Meu site com posts, tutoriais e artigos
- Meu perfil no LinkeDin