Solução para multicolinearidade: Regressão do Componente Principal
Rodrigo H. Ozon
02/09/2020
Resumo
Este tutorial replica o conteúdo presente em Maddala, p. 150-153, 2001, com algumas adaptações.
O método dos componentes principais é uma das opções para solução deste problema, bem como a regressão ridge que pode ser feita no R ou veja aqui sobre a Regressão Ridge no Eviews:
Algumas estimativas podem ser diferentes provavelmente pelas omissões de detalhes a este respeito do próprio autor ou pelos métodos empregados pelo uso de diferentes softwares.
Introdução
Algumas ações corretivas podem ser empregadas para a multicolinearidade, mas agora normalmente, elas provocam alterações nos modelos. Possíveis ações corretivas para a multicolinearidade são:
- Omitir uma ou mais variáveis independentes altamente correlacionadas e identificar outras para ajudar na previsão:
Advertências
Pode causar um erro de especificação ou regressões com poder preditivo baixo.
Pode deixar de fora variáveis que são importantes para o estudo
- Utilizar o modelo de regressão com variáveis independentes muito correlacionadas apenas para fazer previsões.
Advertências
Não tente interpretar os coeficientes de regressão
O conjunto de variáveis explicativas pode perder poder explicativo.
E, ainda:
Utilizar as correlações simples para compreender a relação entre variáveis dependentes e independentes
Usar informação a priori sobre o valor da estimativa dos parâmetros obtida de estudos prévios, prevenindo que o pesquisador aceita parâmetros incorretos.
Transformar a relação funcional (por exemplo, elevando as variáveis ao quadrado ou extraindo o logaritmo).
Utilizar o método de seleção de variáveis stepwise
Verificar a existência de outliers
Aumentar o tamanho da amostra.
Regressão do Componente Principal
Outra solução frequentemente sugerida para o problema de multicolinearidade é a regressão do componente principal, que procede da seguinte forma. Suponha que tenhamos \(k\) variáveis explicativas. Então podemos considerar funções lineares dessas variáveis.
\[ z_{1}=a_{1}x_{1}+a_{2}x_{2}+\ldots+a_{k}x_{k} \]
\[ z_{2}=b_{1}x_{1}+b_{2}x_{2}+\ldots+b_{k}x_{k}\quad\mbox{etc.} \]
Suponha que escolhemos os \(a^{'}s\) de forma que variância de \(z_{1}\) seja maximizada sujeita à condição de que
\[ a^{2}_{1}+a^{2}_{2}+\ldots+a_{k}^{2}=1 \] Isso é chamado condição de normalização. (Isso é necessário pois caso contrário, a variância de \(z_{1}\) pode aumentar indefinidamente.) \(z_{1}\) é, então, chamado de primeiro componente principal. É a função linear dos \(x^{'}s\) que tem maior variância (sujeito à regra de normalização).
Discutiremos os principais destaques e usos desse método, os quais são fáceis de se compreender sem o uso de álgebra matricial. Além disso, para se usar o método existem programas de computador disponíveis que fornecem os componentes principais (\(z^{'}s\)), dado qualquer conjunto de variáveis \(x_{1},x_{2},\ldots,x_{k}\).
Esse processo de maximização da variância da função linear \(z\) sujeito à condição de que a soma dos quadrados dos coeficientes dos \(x^{'}s\) é igual a 1 produz \(k\) soluções. Correspondendo a isso, construímos \(k\) funções lineares \(z_{1},z_{2},\ldots,z_{2},\) denominadas de componentes principais dos \(x^{'}s\). Elas podem ser ordenadas de forma que
\[ var(z_{1})>var(z_{2})>\ldots>var(z_{k}) \] \(z_{1}\), que tem a maior variância, é chamada de primeiro componente principal, \(z_{2}\), que tem a segunda maior variância, é chamada de segundo componente principal e assim por diante. Esses componentes principais têm as seguintes propriedades:
\(var(z_{1})+var(z_{2})+\ldots+var(z_{k})=var(x_{1})+var(x_{2})+\ldots+var(x_{k})\)
Diferentemente dos \(x^{'}s\), que são correlacionados, os \(z^{'}s\) são ortogonais e não-correlacionados. Logo, existe zero multicolinearidade entre os \(z^{'}s\).
Por vezes é sugerido que em vez de se regredir \(y\) em \(x_{1},x_{2},\ldots,x_{k}\), devemos regredir \(y\) em \(z_{1},z_{2},\ldots,z_{k}\). Mas isso não é um problema para solução da multicolinearidade. Se regredirmos \(y\) nos \(z^{'}s\) e, então, substituimos os valores dos \(z^{'}s\) nos termos dos \(x^{'}s\), acharemos finalmente as mesmas respostas que antes. O fato de os \(z^{'}s\) serem não-correlacionados não significa que acharemos melhores estimativas dos coeficientes na equação de regressão original. Dessa forma, faz sentido usar os componentes principais apenas se regredirmos \(y\) em um subconjunto dos \(z^{'}s\). Mas esse procedimento também tem problemas. São eles:
O primeiro componente principal, \(z_{1}\), embora tenha a maior variância, não precisa ser o mais correlacionado com \(Y\). Na verdade, não há relação necessária entre a ordem dos componentes principais e o grau de correlação com a variável dependente \(Y\).
Pode-se pensar em se escolher apenas aqueles componentes principais que têm correlação elevada com \(Y\) e em descartar o restante, mas o mesmo procedimento pode ser usado com o conjunto de variáveis original \(x_{1},x_{2},\ldots,x_{k}\) escolhendo primeiro a variável com a maior correlação com \(Y\), depois a com maior correlação parcial e assim por diante. Isso é o que os “programas de regressão” passo a passo fazem.
Por vezes é sugerido que em vez de se regredir \(y\) em \(x_{1},x_{2},\ldots,x_{k}\), devemos regredir \(y\) em \(z_{1},z_{2},\ldots,z_{k}\). Mas isso não é uma solução para o problema da multicolinearidade. Se regredirmos \(y\) nos \(z^{'}\) nos termos dos \(x^{'}\), acharemos finalmente as mesmas respostas de antes. O fato de os \(z^{'}s\) serem não-correlacionados não singifica que acharemos melhores estimativas dos coeficientes na equação de regressão original. Dessa forma, faz sentido usar os componentes principais apenas se regredirmos \(y\) em um subconjunto dos \(z^{'}s\). Mas esse procedimento também tem problemas. São eles:
O primeiro componente principal \(z_{1}\), embora tenha a maior variância, não precisa ser o mais correlacionado com \(y\). Na verdade, não há relação necessária entre a ordem dos componentes principais e o grau de correlação com a variável dependente \(y\).
Pode-se pensar em se escolher apenas aqueles componentes principais que têm correlação elevada com \(y\) e em se descartar o restante, mas o mesmo procedimento pode ser usado com o conjunto de variáveis original \(x_{1},x_{2},\ldots,x_{k}\) escolhendo primeiro a variável com maior correlação com \(y\), depois a com maior correlação parcial e assim por diante. Isso é o que os “programas de regressão” passo a passo fazem.
As combinações lineares dos \(z^{'}s\) com frequência não tem sentido econômico. O que significa, por exemplo, 2(renda) +3(preço) ? Essa é uma das falhas mais importantes do método.
Alterar as unidades de medição dos \(x^{'}s\) transformará os componentes principais. Esse problema pode ser evitado se todas as variáveis forem padronizadas para terem variância unitária.
No entanto, o método do componente principal tem alguma utilidade nos estágios explicativos da investigação. Suponha, por exemplo, que haja muitas taxas de juros no modelo (como todas são medidas nas mesmas unidades, não há problema de escolha de unidade de medida). Se a análise do componente principal mostrar dois componentes principais respondem por 99% da variação das taxas de juros e se, olhando para os coeficientes, conseguirmos identificá-lo como componentes de curto prazo e de longo prazo poderemos argumentar que existem apenas duas variáveis “latentes” que respondem por todas as variações das taxas de juros. Portanto, o método do componente principal nos oferecerá alguma direção para a pergunta: “quantas fontes independentes de variação existem ?” Além disso, se pudermos dar uma interpretação econômica aos componentes principais, isso será útil.
Ilustramos o método com referência a um conjunto de dados de Mallinvaud (E. Mallinvaud, Statistical Methods of Econometrics, 2a. ed., Amsterdã: North-Holland, 1970, p. 19). Escolhemos esses dados porque eles foram usados por Chatterjee Price (in Regression Analysis, p. 161) para ilustrar o método do componente principal.
Você pode baixar a planilha Excel com os dados aqui.
Primeiro estimamos uma função de demanda por importação. Ao regredir \(y\) em \(x_{1},x_{2},x_{3}\) acham-se os seguintes resultados:
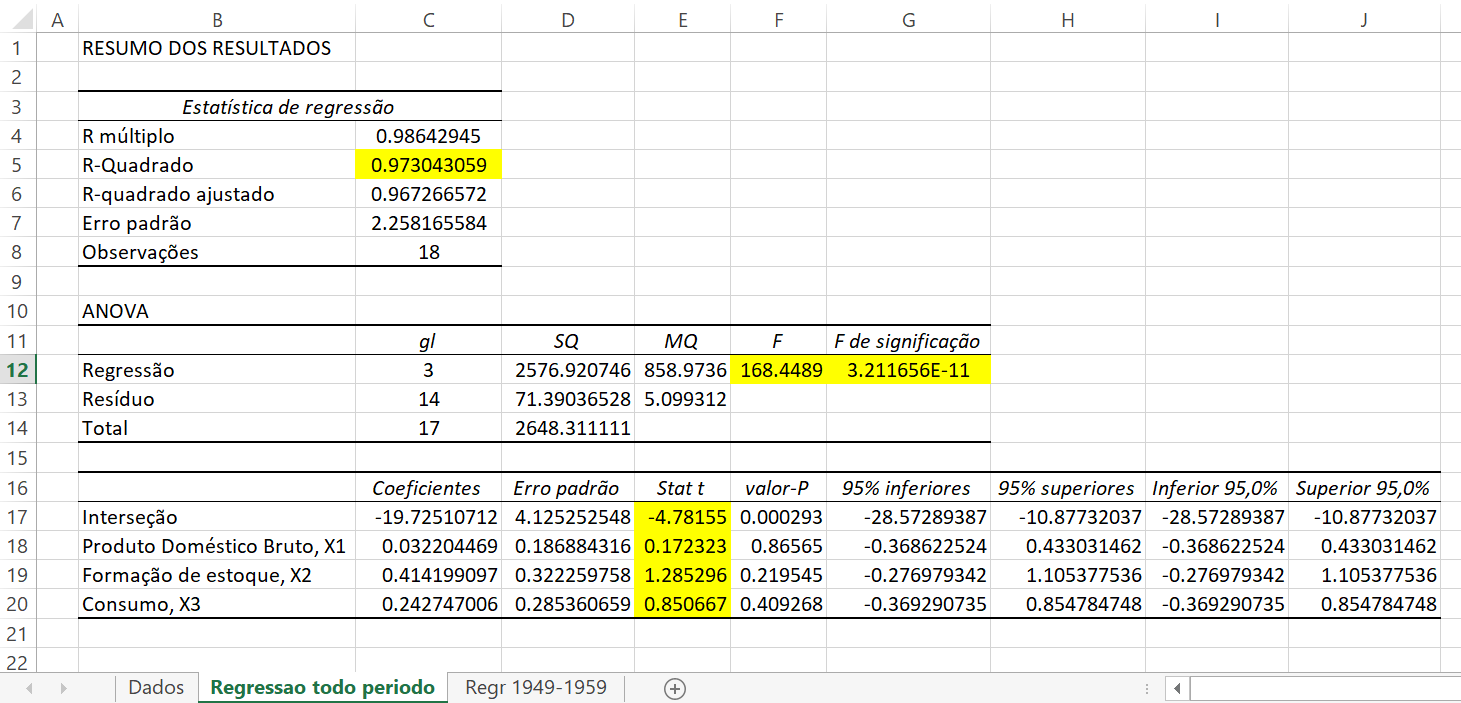
Resultados da Regressão com a série completa
O \(R^{2}\) é muito elevado e a razão \(F\) é altamente significativa, mas todas as razões \(t\) individuais são insignificantes. Isso é evidência do problema da multicolinearidade. Chatterjee e Price argumentam que antes que qualquer análise adicional seja feita, devemos olhar para os resíduos dessa equação. Eles acham (veja o gráfico de resíduos) um padrão definido – os resíduos declinam até 1960 e então aumentam.
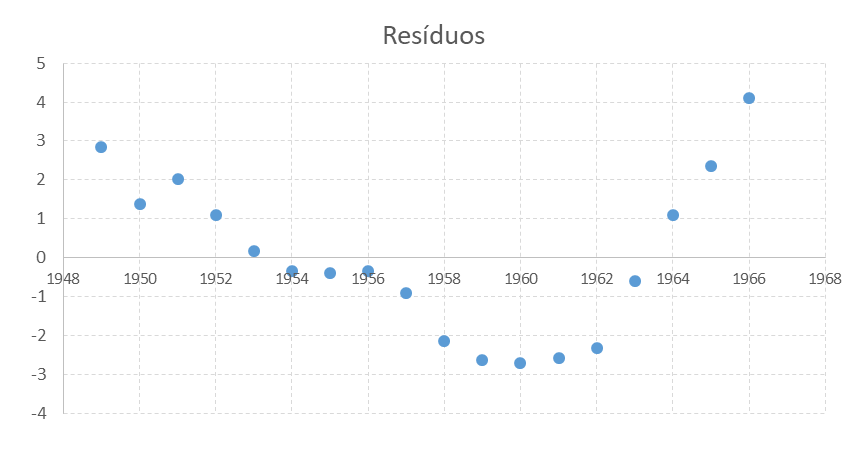
Padrão de resíduos da regressão com a série completa
Chaterjee e Price argumentam que a dificuldade desse modelo é que o Mercado Comum Europeu começou a operar em 1960, causando mudanças nas relações entre importação e exportação. Portanto, eles excluem os anos posteriores a 1959 e consideram apenas os 11 anos do período 1949–1959. Agora os resultados da regressão são os seguintes:
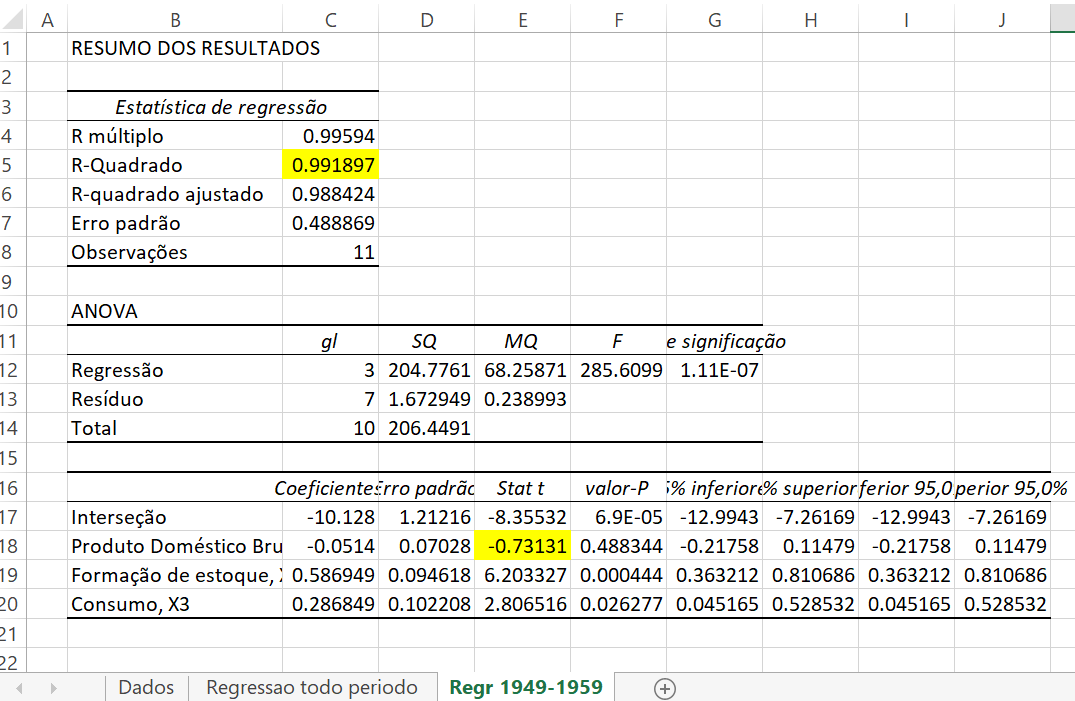
Regressão para 1949-1959
Como podemos ver no gráfico de resíduos a seguir, não encontramos um padrão sistemático
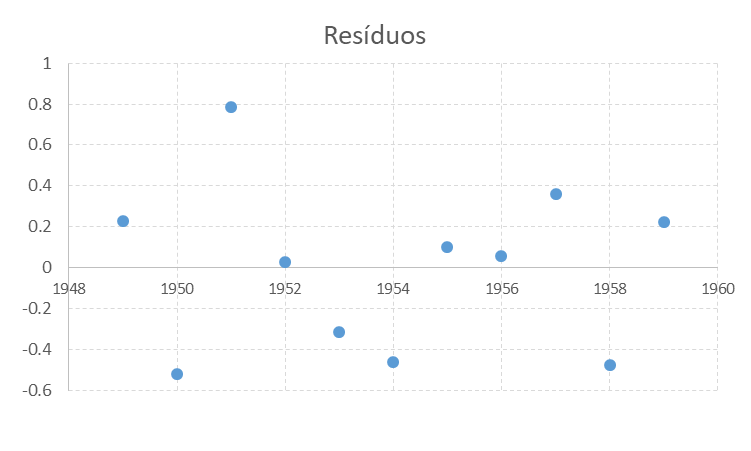
Padrão residual da Regressão para 1949-1959
de forma que podemos prosseguir.
Embora o \(R^{2}\) seja muito elevado, o coeficiente de \(x_{1}\) não é significante (\(t=-0,731305765\) e valor\(-p=0,488344308\)). Existe, por conseguinte, um problema de multicolinearidade.
Para ver o que deve ser feito sobre isso, primeiro olhamos para as correlações simple entre as variáveis explicativas:

Matriz de correlação das explicativas para a Regressão para 1949-1959
Suspeitamos que a alta correlação presente nos dados de Consumo (\(X3\)) com Produto Doméstico Bruto (\(X1\)), possa ser a causa do problema.
A análise de componentes principais ajuda ? Vamos para o primeiro passo, rumando para a obtenção dos valores dos componentes principais no pacote estatístico R:
library(readxl)
url<-"https://github.com/rhozon/Introdu-o-Econometria-com-Excel/blob/master/Maddala,%20p.%20151.xlsx?raw=true)"
dados <- tempfile()
download.file(url, dados, mode="wb")
dados<-read_excel(path = dados, sheet = 1)
dados## # A tibble: 11 x 9
## Ano Y X1 X2 X3 Ypadr X1padr X2padr X3padr
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1949 15.9 149. 4.2 108. -1.32 -1.51 0.546 -1.53
## 2 1950 16.4 161. 4.1 115. -1.21 -1.11 0.485 -1.21
## 3 1951 19 172. 3.1 123. -0.636 -0.770 -0.121 -0.801
## 4 1952 19.1 176. 3.1 127. -0.614 -0.636 -0.121 -0.622
## 5 1953 18.8 181. 1.1 132. -0.680 -0.460 -1.33 -0.370
## 6 1954 20.4 191. 2.2 138. -0.328 -0.130 -0.667 -0.0987
## 7 1955 22.7 202. 2.1 146 0.178 0.250 -0.728 0.304
## 8 1956 26.5 212. 5.6 154. 1.01 0.594 1.39 0.696
## 9 1957 28.1 226. 5 162. 1.37 1.05 1.03 1.09
## 10 1958 27.6 232. 5.1 164. 1.26 1.24 1.09 1.19
## 11 1959 26.3 239 0.7 168. 0.970 1.48 -1.58 1.35Então seleciono somente as variáveis explicativas e em seguida calculo as variâncias de cada uma das três variáveis
library(dplyr)##
## Attaching package: 'dplyr'## The following objects are masked from 'package:stats':
##
## filter, lag## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, unionexplicativas<-dados%>%
select(X1,X2,X3)
vars <- apply(explicativas, 2, var)
vars## X1 X2 X3
## 899.9709 2.7200 425.7785A maior fração da variância explicada entre essas variáveis é 70%, e a menor é quase 0% (X2). Também podemos calcular essas frações para subconjuntos de variáveis. Por exemplo, as variáveis 1 e 3 juntas explicam 99,94% da variância total, e as variáveis 1 e 2 explicam 70,02%.
A análise de componentes principais calcula um novo conjunto de variáveis (“componentes principais”) e expressa os dados em termos dessas novas variáveis. Consideradas em conjunto, as novas variáveis representam a mesma quantidade de informação que as variáveis originais, no sentido de que podemos restaurar o conjunto de dados original do transformado.
Além disso, a variância total permanece a mesma. No entanto, é redistribuído entre as novas variáveis da forma mais “desigual”: a primeira variável não apenas explica a maior variância entre as novas variáveis, mas também a maior variância que uma única variável pode possivelmente explicar.
vars/sum(vars)## X1 X2 X3
## 0.677449456 0.002047469 0.320503075De forma mais geral, os primeiros componentes principais (onde \(k\) pode ser 1, 2, 3 etc.) explicam a maior variância que qualquer \(k\) variável pode explicar, e as últimas \(k\) variáveis explicam a menor variância que qualquer \(k\) variável pode explicar, sob algumas restrições gerais. (As restrições garantem, por exemplo, que não podemos ajustar a variância explicada de uma variável simplesmente escalando-a.)
pca <- prcomp(explicativas, retx=T)
expl_transformada <- pca$x
expl_transformada## PC1 PC2 PC3
## [1,] -55.243186 0.8526477 -0.6319214
## [2,] -41.641198 0.4642629 -1.7916913
## [3,] -28.396312 -0.2823642 -0.5011266
## [4,] -23.004179 -0.1131437 0.2645521
## [5,] -15.693755 -1.7829447 1.9673323
## [6,] -4.361502 -0.9482986 0.7576149
## [7,] 9.734530 -0.9774781 1.1588999
## [8,] 22.815447 2.6055542 1.1976004
## [9,] 38.749791 1.7756696 0.3621647
## [10,] 44.662808 1.4979238 -1.2531020
## [11,] 52.377555 -3.0918290 -1.5303231Estas são as variâncias de amostra das novas variáveis.
vars_transformadas <- apply(expl_transformada, 2, var)
# ou: pca$sdev^2
vars_transformadas## PC1 PC2 PC3
## 1324.168516 2.781380 1.519559Observe que sua soma, a variância total, é a mesma das variáveis originais: 2,99.
E essas são as mesmas variâncias divididas pela variância total, ou seja, quanto da variância total cada nova variável explica:
vars_transformadas/sum(vars_transformadas)## PC1 PC2 PC3
## 0.996762486 0.002093673 0.001143842os componentes principais (obtidos pelo pacote Eviews) são:
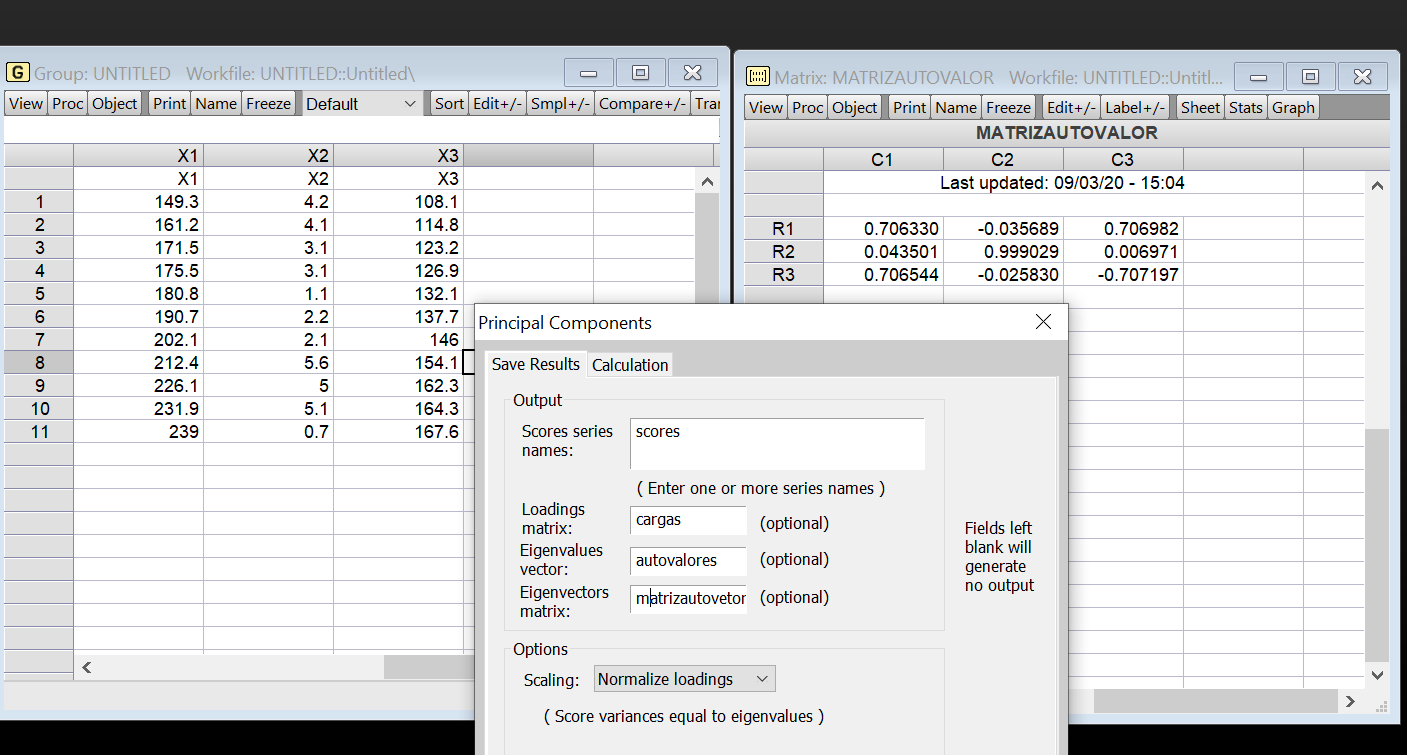
Matriz de Autovalores para os dados 1949-1959
Obtemos assim os mesmos valores encontrados por Maddala, p. 152, 2001:
\[ z_{1}=0,706330X_{1}+0,043501X_{2}+0,706544X_{3} \] \[ z_{2}=-0,035689X_{1}+0,999029X_{2}-0,025830X_{3} \] \[ z_{3}=0,706982X_{1}+0,006971X_{2}-0,707197X_{3} \] onde \(X_{1},X_{2},X_{3}\) são os valores normalizados de \(x_{1},x_{2},x_{2}\). Isto é, \(X_{1}=(x_{1i}-\overline{x_{1}})/\sigma(x_{1})\) e \(X_{2}=(x_{2i}-\overline{x_{2}})/\sigma(x_{2})\) e \(X_{3}=(x_{3i}-\overline{x_{3}})/\sigma(x_{3})\) onde \(\overline{x_{1}}, \overline{x_{2}} \,\,e\,\,\overline{x_{3}}\) são as médias aritméticas de \(x_{1},x_{2},x_{3}\) respectivamente. Logo
\[ var(X_{1})=var(X_{2})=var(X_{3})=1 \]
As variâncias dos componentes principais são
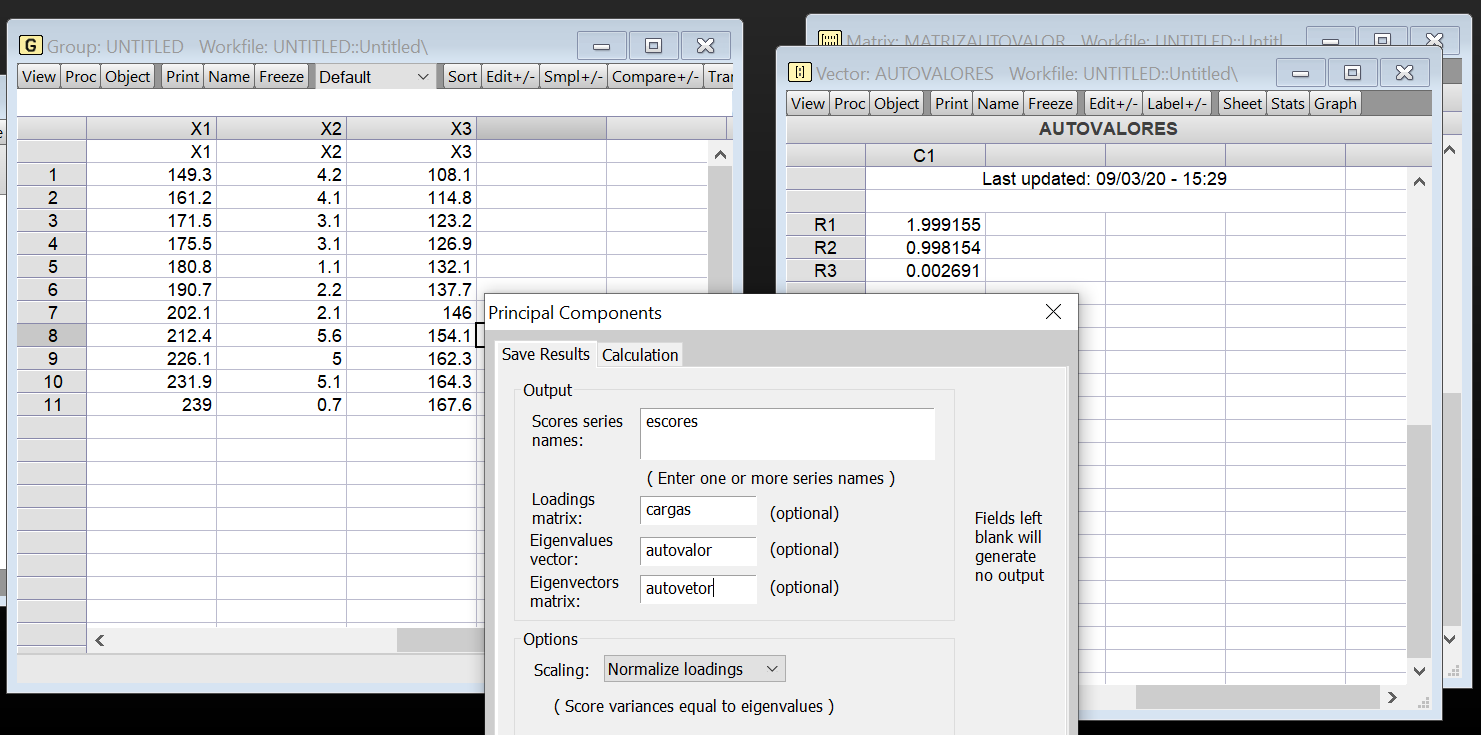
Matriz de Autovetores para os dados 1949-1959
então
\[ var(z_{1})=1,99915493449973\quad var(z_{2})=0,9981541760451606\quad var(z_{3})=0,002690889455111145 \] Note que \(\sum var(z_{i})=\sum var(X_{i})=3\).O fato de que \(var(z_{3})=0\) identifica aquela função linear como causa da multicolinearidade. Nesse exemplo, há apenas uma função linear desse tipo. Em alguns exemplos pode haver mais. Como \(E(X_{1})=E(X_{2})=E(X_{3})=0\) por causa da normalização, os \(z^{'}s\) têm média zero. Assim, \(z_{3}\) tem média zero e sua variância também está perto de zero. Portanto, podemos afirmar que \(z\simeq 0\). Olhando para os coeficientes \(X^{'}s\), podemos dizer que (ignorando os coeficientes muito pequenos)
\[ z_{1}\simeq 0,7063(X_{1}+X_{3}) \] \[ z_{2}\simeq X_{2} \] \[ z_{3}\simeq 0,707(X_{3}-X_{1}) \] \[ z_{3}\simeq 0\quad\mbox{logo}\quad X_{1}\simeq X_{3} \] Na verdade, teríamos achado os mesmos resultados da regressão de \(X_{3}\) em \(X_{1}\). O coeficiente de regressão é \(r_{13}=0,99726\). (Observe que \(X_{1}\) e \(X_{3}\) estão em forma padronizada e, por consequência, o coeficiente de regressão é \(r_{13}\).)
Em termos de variáveis originais (não normalizadas), a regressão de \(x_{3}\) em \(x_{1}\) é: (erro padrão entre parêntesis)
\[ x_{3}=6,258606642+0,685940354x_{1}\quad R^{2}=0,99452889\\ \quad(0,0169588) \]
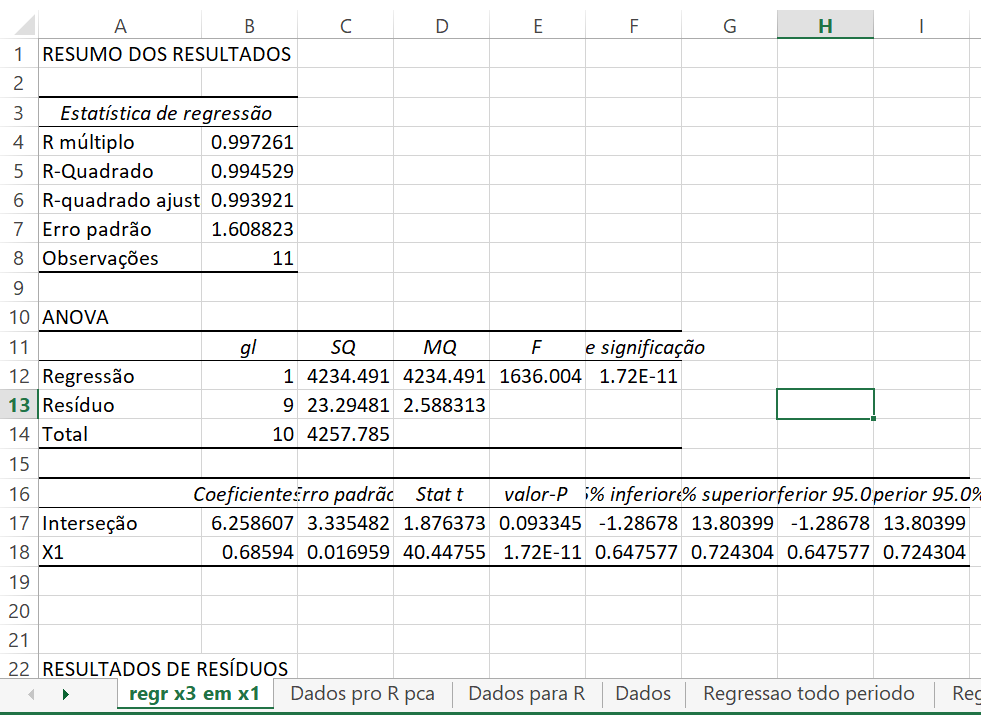
Regressão de \(X_{3}\) em \(X_{1}\) para os dados 1949-1959
Não obtivemos, nesse exemplo, mais informação a partir da análise do componente principal do que do estudo da correlação simples. De qualquer forma, qual é a solução agora ? Dado que existe uma relação quase exata entre \(x_{3}\) em \(x_{1}\), não podemos esperar estimar os coeficientes de \(x_{1}\) e \(x_{3}\) separadamente. Se a equação original for
\[ y=\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}+\beta_{3}x_{3}+u \] então, substituindo por \(x_{3}\) os termos de \(x_{1}\), temos
\[ y=(\beta_{0}+6,258\beta_{3})+(\beta_{1}+0,686\beta_{3})x_{1}+\beta_{3}x_{3}+u \]
Isso fornece as funções lineares dos \(\beta^{'}s\) que são estimáveis. São eles (\(\beta_{0}+6,258\beta_{3}\)),(\(\beta_{1}+0,686\beta_{3}\)) e \(\beta_{2}\). Da regressão de \(y\) em \(x_{1}\) e \(x_{2}\), acham-se os seguintes resultados:
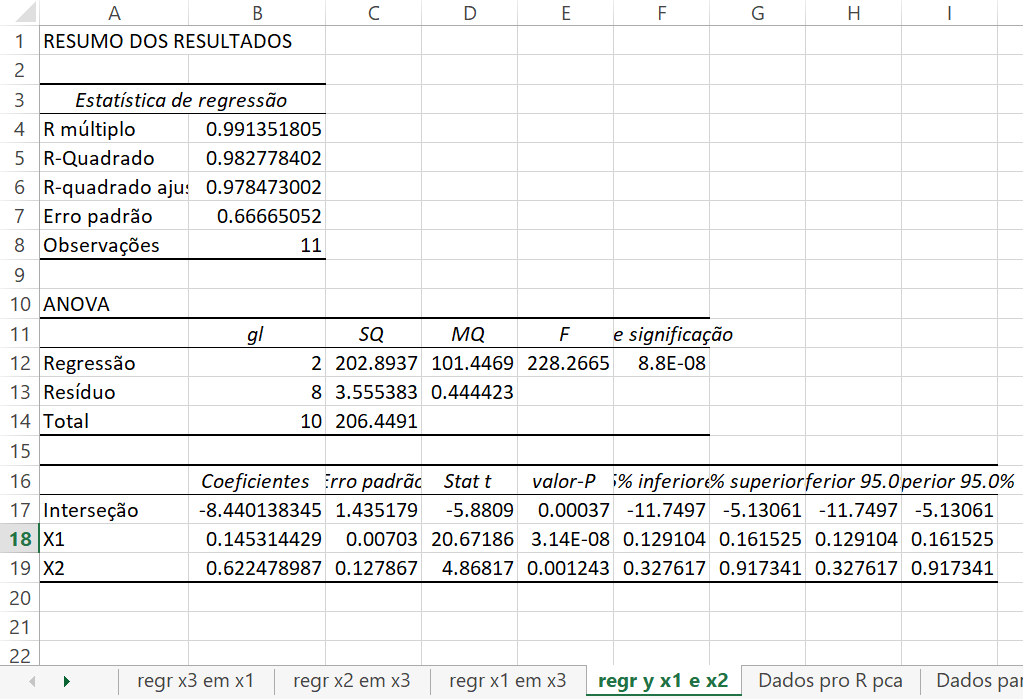
Regressão de \(y\) em \(X_{1}\) e \(X_{2}\) para os dados 1949-1959
Obviamente, podemos estimar uma regressão de \(x_{1}\) e \(x_{3}\).
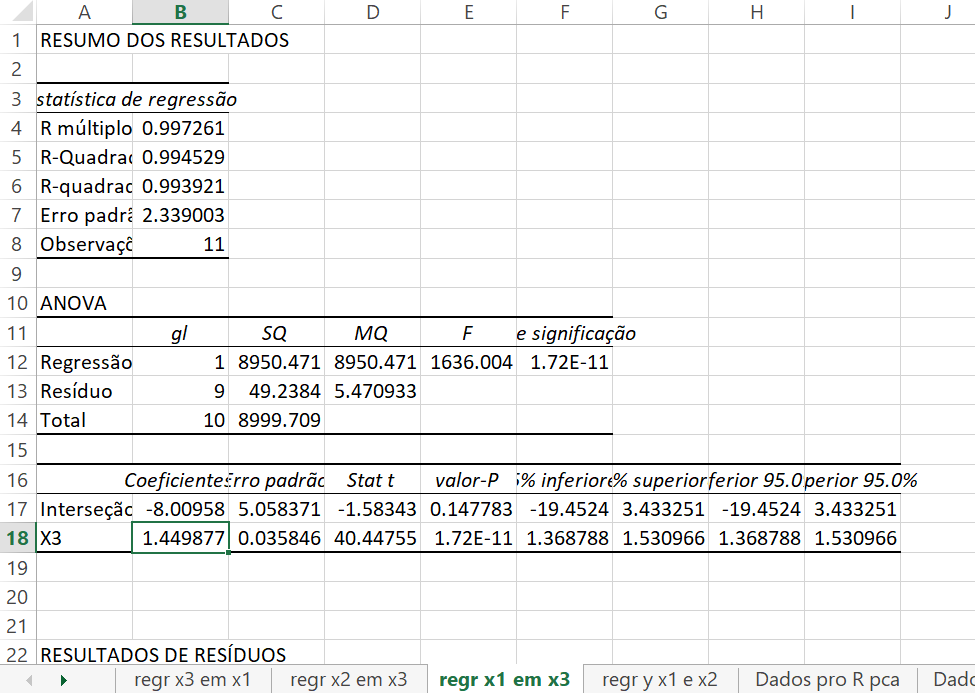
Regressão de \(X_{1}\) em \(X_{3}\) para os dados 1949-1959
O coeficiente de regressão é 1,45. Agora, substituímos por \(x_{1}\) e estimamos uma regressão de \(y\) em \(x_{2}\) e \(x_{3}\). Os resultados que achamos são ligeiramente melhores (temos um \(R^{3}\) maior). Os resultados são:
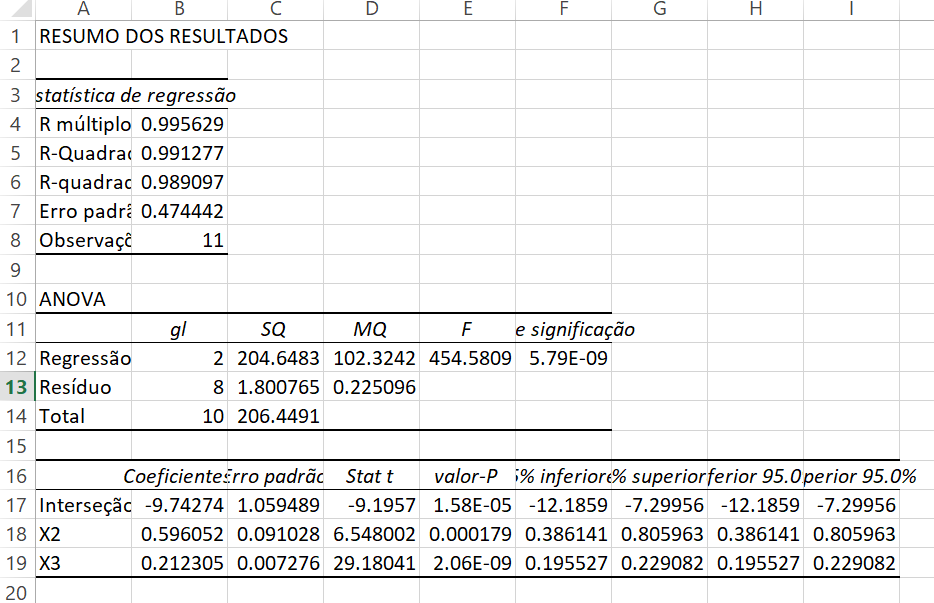
Regressão de \(Y\) em \(X_{2}\) e \(X_{3}\) para os dados 1949-1959
O coeficiente de \(x_{3}\) agora é (\(\beta_{3}\)+1,45).
Podemos achar estimativas separadas de \(\beta_{1}\) e \(\beta_{3}\) apenas se tivermos alguma informação a priori. Como indica esse exemplo, a multicolinearidade implica que não podemos estimar coeficientes individuais com boa precisão, mas podemos estimar algumas funções lineares dos parâmetros com boas precisão. Se quisermos estimar os parâmetros individuais, precisaremos de alguma informação a priori. Mostraremos que o uso dos componentes principais implica a utilização de alguma informação a priori sobre as restrições dos parâmetros.
Suponha que consideremos regredir \(y\) nos componentes principais \(z_{1}\) e \(z_{2}\) (\(z_{3}\) é omitido porque ele é quase zero). Vimos que \(z_{1}=0,7(X_{1}+X_{3})\) e \(z_{2}=X_{2}\). Precisamos transformá-los nas variáveis originais. Temos
\[ z_{1}=0,7\left(\frac{x_{1i}-\overline{x_{1}}}{\sigma_{1}}+\frac{x_{3i}-\overline{x}}{\sigma_{3}} \right) \] \[ \quad = \frac{0,7}{\sigma_{1}}\left(x_{1}+\frac{\sigma_{1}}{\sigma_{3}}x_{3}\right)+\mbox{uma constante} \] \[ \quad z_{2}=\frac{1}{\sigma_{2}}(x_{2}-\overline{x_{2}}) \] Portanto, usar \(z_{2}\) como um regressor é equivalente a usar \(x_{2}\), e usar \(z_{1}\) é equivalente a usar (\(x_{1}+(\sigma_{1}/\sigma_{3})x_{3}\)). Logo, a regressão do componente principal equivale a regredir \(y\) em \((x_{1}+(\sigma_{1}/\sigma_{3})x_{3})\) e \(x_{2}\). Em nosso exemplo, \(\sigma_{1}/\sigma_{3}=1,453859199\). Esses resultados são
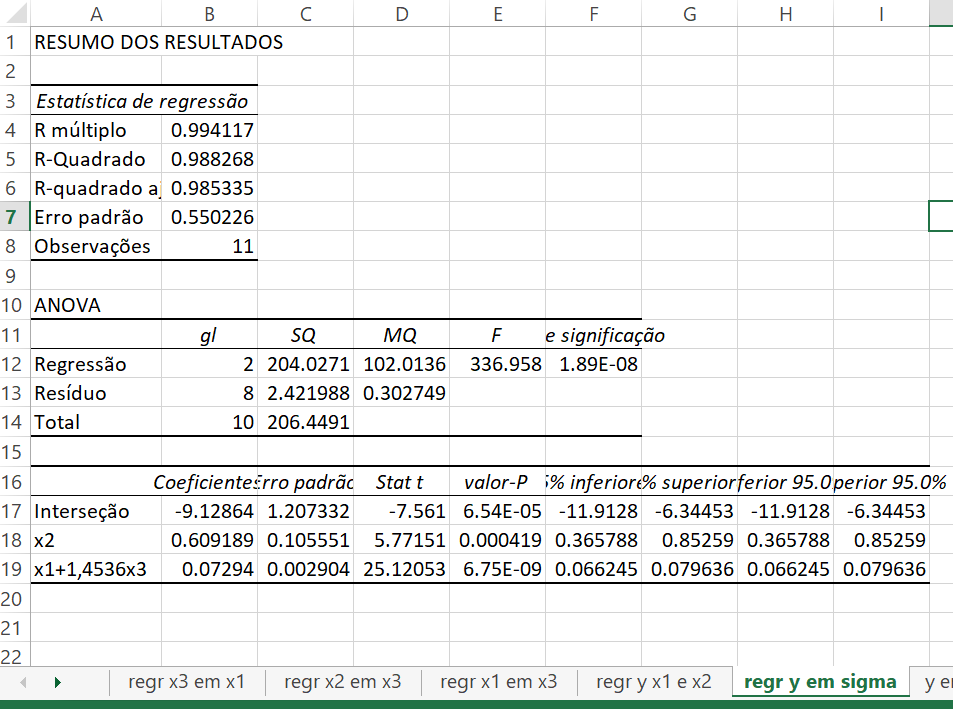
Regressão de \(Y\) em \(X_{1}+1,4536X_{3}\) e \(X_{2}\) para os dados 1949-1959
Essa é a equação de regressão que teríamos estimado se assumíssemos que \((\beta_{3}=(\sigma_{1}/\sigma_{3})\beta_{1})=1,4536\beta_{1}\). Assim, a regressão do componente principal equivale, nesse mesmo exemplo, ao uso da informação a priori \(\beta_{3}=1,4536\beta_{1}\).
Se todos os componentes principais forem usados, isso é exatamente equivalente a usar o conjunto de variáveis explicativas original. Se alguns componentes principais forem omitidos, isso equivale a usar alguma informação a priori nos \(\beta^{'}s\). Em nosso exemplo, a pergunta é se o pressuposto \(\beta_{3}=1,45\beta_{1}\) tem sentido econômico. Sem mais dados desagregados que dividam as importações em bens de consumo e bens de produção, não podemos dizer nada. De qualquer forma, com 11 observações não podemos esperar responder a mais perguntas. O propósito de nossa análise tem sido meramente mostrar o que é a regressão do componente principal e que ela implica alguma informação a priori.
Exercício proposto
Quando você estima um modelo autoregressivo para esses dados, como a multicolinearidade pode viesar os resultados ?
Referências
Maddala, G.S. Introdução à Econometria. Third Edition, 2001.