Previsão (forecasting) de séries temporais financeiras com o Facebook Prophet
Rodrigo Hermont Ozon
junho 18, 2021
Economic Time Series Forecasting
A maioria dos meus alunos e das pessoas que me conhecem sabem que eu tenho uma curiosidade enorme pelas Sagradas Escrituras, sua história de diferentes interpretações, suas maravilhas e principalmente por seus mistérios. Dentre um deles que me desperta extremo interesse aquele que diz respeito ao atributo de onisciência de Deus me encanta, pois quem crê sabe que somente Ele sabe o que será do futuro com 100% de certeza e do mesmo modo, ele é eterno! Ou seja, a dimensão de tempo e espaço em que Deus É, difere muito do nosso _chronos x kairós_. Com o lançamento do algoritmo ``Prophet`` para R e Python lançado pela equipe do Facebook, fica a dúvida de todo econometrista ou futurólogo analista de séries temporais... se a capacidade de prever o que irá acontecer fora da amostra para cenários onde os dados são não-lineares, cheios de outliers (soluços), agrupamentos de volatilidades e quebras estruturais, fora as componentes tradicionais de ciclo, tendência e sazonalidade (quando identificadas) são capturadas e modeladas e desenhadas com grau de erro pequeno no futuro próximo.
Anunciai-nos as coisas que ainda hão de vir, para que saibamos que sois deuses; ou fazei bem, ou fazei mal, para que nos assombremos, e juntamente o vejamos. Isaías 41:23

\[\\[1in]\]
Intro
Segundo os autores do pacote para R, o prophet:
Implements a procedure for forecasting time series data based on an additive model where non-linear trends are fit with yearly, weekly, and daily seasonality, plus holiday effects. It works best with time series that have strong seasonal effects and several seasons of historical data. Prophet is robust to missing data and shifts in the trend, and typically handles outliers well.
Não pretendo aqui fazer uma reprodução extensiva da construção metodológica do prophet, pois isso está bem claro na publicação de seus criadores em https://peerj.com/preprints/3190/. Só a título de ilustração os autores formalizam o prophet como:
\[ y_t = g(t) + s(t) + h(t) + \epsilon_t \] Onde:
\(g(t)\) representa a componente de crescimento ou tendência linear; (growth)
\(s(t)\) padrões de sazonalidade; (seasonality)
\(h(t)\) efeitos de feriados; (holidays)
\(\epsilon_t\) termo de erro do tipo ruído branco (white noise)
Sendo que:
\(g(t)\) é selecionada automaticamente se não for especificada (leave in blank);
\(s(t)\) são os termos de Fourier dos períodos relevantes. Para sazonalidade anual usa-se 10 e 3 para semanal;
\(h(t)\) os feriados são variáveis dummies
As quebras estruturais e inversões de tendência/trajetória são estimadas com métodos bayesianos e demais características do modelo;
A intenção deles é “make it easier for experts and non-experts to make high-quality forecasts that keep up with demand.” Ou seja, parece que a implementação deste algoritmo pronto resolve a maioria do trabalho dos analistas em análises exploratórias, tratamento de dados e ajustes de diferentes tipos de modelos a características comuns inerentes aos dados investigados. Todavia é possível customizar alguns inputs de parâmetros, como indicar a presença de períodos sazonais (semanal ou anual), feriados e changepoints (quebras estruturais). (https://facebook.github.io/prophet/)
Os criadores Taylor e Letham (2017), utilizam vastamente o pacote Stan para sua interface, onde métodos bayesianos são vastamente empregados, o que me parece um ponto de melhoria no ensino e aplicação da econometria nas universidades tupiniquins, uma vez que a abordagem frequentista dela ainda é muito proeminente nos livros-texto traduzidos. Ademais ressaltamos a falta de ensinos da econometria com vasto uso de recursos computacionais nas universidades por aqui, o que noto como algo extremamente desanimador para o estudante num primeiro contato com a disciplina.
Utilizei o stan para um exemplo de aplicação simples (com dados artificiais) demonstrando a vantagem significativa no uso da inferência bayesiana contra a frequentista num modelos de elasticidade-preço da demanda que você pode consultar aqui. caso tenha interesse em conhecer um pouco mais.
De toda maneira deixo aqui as minhas recomendações de literatura (para aqueles que cursaram Joel Idiomas) para esse tema:
An introduction to Bayesian inference in econometrics, Arnold Zellner, um clássico e talvez a obra pioneira na inferência bayesiana na econometria;
Bayesian econometrics, Gary Koop, talvez o livro mais popular na literatura e mais conceituado sobre o tema;
Bayesian Econometric Methods (Econometric Exercises) Gary Koop, Dale J. Poirier, Justin L. Tobias, para aquele estudante “guerreiro” que tem a curiosidade de aprender a respeito desses métodos com o R na sua linha frente (apesar de na minha humilde opinião, ele falhar bastante nisso não colocando alguns scripts como solução)
Bayesian Data Analisys, Andrew Gelman, et. alli Leitura com robustez teórica bem fundamentada de inferência bayesiana com alguns scripts do R no final. Senti um pouco da falta de alguns exemplos com dados prontos do R para alguns casos.]
Bayesian Computation With R, Jim Albert (auth.), uma leitura um pouco mais light no rigor teórico, mas com um pouco mais de exemplos aplicados interessantes.
Em linhas gerais podemos diferenciar as abordagens de método considerando que: os frequentistas assumem que os parâmetros do modelo são fixos e os dados são aleatórios, enquanto os bayesianos assumem que os dados são fixos e os parâmetros do modelo são aleatórios. Isso pode ser visto na interpretação de um valor p. Dito de outra forma, os bayesianos estão interessados em determinar a faixa de valores dos parâmetros que dariam origem ao seu conjunto de dados observados
Uma interpretação interessante aparece na diferença do intervalo de confiança (frequentista) e do intervalo confiável (bayesiano). Um intervalo confiável será muito semelhante a um intervalo de confiança. Um intervalo de confiança nos informa a probabilidade de que um intervalo contenha o valor verdadeiro. No entanto, o intervalo de confiança não pode nos dizer nada sobre a probabilidade de quaisquer valores específicos para o parâmetro de interesse. Os intervalos confiáveis nos dizem quais são os valores prováveis. Isso nos permite fazer inferências sobre os valores reais dos parâmetros, ao invés dos limites dos intervalos.
Muitas vezes, pode ser o caso, mas as inferências são muito diferentes. No cenário bayesiano, podemos perguntar qual é a probabilidade de que o parâmetro esteja entre 0,60 e 0,65, e vemos uma chance de 31% de o valor verdadeiro estar nessa faixa. Como faríamos algo semelhante com intervalos de confiança de um modelo frequentista? Não podemos. Apenas os métodos bayesianos nos permitem fazer inferências sobre os valores reais do parâmetro.
Sem extender muito o assunto a respeito das distinções de método frequentista e bayesiano, (para maiores detalhes consulte Orloff e Blum, 2014) caímos no forte questionamento a respeito de muitos modelos de projeção de séries temporais econômicas:
"A experiência prática com o modelo BVAR tem sido muito boa. Dela se tem produzido previsões melhores comparando-se com muitos modelos de equações simultâneas estruturais. Isso foi, contudo, criticado como "econometria não-teórica", simplesmente porque não usa nenhuma teoria econômica." (Maddala, p. 292, 2003)
Eu como grande entusiasta no uso de modelos VAR e de suas funções de impulso-resposta, gostava muito de estudar as direções de impacto e reajuste as trajetórias “de equilíbrio” de algumas séries temporais econômicas em questão, mesmo sabendo da extrema complexidade e dificuldade envolvida na modelagem dos reais movimentos causadores de tais oscilações. Na minha monografia de graduação utilizei uma combinação de GARCH com VAR (não bayesiano) para avaliação da dinâmica das séries de preços do petróleo no mercado internacional, utilizando as teorias de expectativas dos agentes com a replicação da News Impact Curve do seminal trabalho do prof. Robert Engle.
Sabemos que a grande maioria dos modelos de projeção para o futuro fora da amostra são ateóricos na sua construção. Muitos deles são univariados, outros múltiplos, mas como acredito que agora posso fazer uso da fala do renomado econometrista do MIT, prof. Josh Angrist, ressalto a sua crítica construtiva quando ele distingue a econometria do pop data science:
"Eu diria que a principal diferença é a abordagem do problema da previsão. Os cientistas de dados geralmente se preocupam com as abordagens do tipo de ajuste de curva para a previsão. Portanto, qualquer modelo que se adapte bem aos dados servirá. Se é uma experiência passada, podemos estar interessados em usá-la para extrapolar para o futuro. Grande parte da agenda de ciência de dados está ligada aos problemas de marketing de alguém. Você está tentando descobrir quem comprará algo, quem tomará alguma ação. A econometria, na minha opinião, lida com uma classe de problemas mais difícil. Econometristas estão mais preocupados com relacionamentos causais. Em outras palavras, se manipularmos algo, por exemplo, seguro de saúde ou política monetária, como será o mundo em resposta a essa mudança? Não assumimos que o passado seja um bom guia para isso, porque entendemos que a variação e a variável estão associadas a muitas variáveis potenciais de confusão - diríamos outras coisas em movimento que talvez também afetem os resultados. A simples relação observada geralmente é enganosa, porque há fatores que não são bem controlados, e temos em mente que existe um projeto de pesquisa que envolve mais do que o ajuste de curvas De fato, somos bastante indiferentes ao ajuste de curvas na economia. Acho que queremos saber, por exemplo, se importa se você estuda em uma faculdade particular cara - isso muda seu curso de vida na forma de ganhos mais altos? Essa não é realmente uma questão de ajuste de curva, é uma questão causal."
(Josh Angrist in Mastering Econometrics)
Exemplo de aplicação para uma série temporal financeira
Conforme destaca o prof. Pedro Morettin em seu renomado livro Econometria Financeira:
Séries econômicas e financeiras apresentam algumas características que são comuns a outras séries temporais, como: (a) tendências; (b) sazonalidade; (c) pontos influentes (atípicos); (d) heteroscedasticidade condicional; (e) não-linearidade. O leitor está, certamente, familiarizado com as caracteríticas acima; para detalhes, veja Franses (1998). Dessas, a última talvez seja a mais complicada de definir. De um modo bastante geral, podemos dizer que uma série econômica ou financeira é não-linear quando responde de maneira diferente a choques grandes ou pequenos, ou ainda, a choques negativos ou positivos. (Morettin, p. 18, 2006)
A maioria dos trabalhos aplicados para esse tipo de dado utiliza modelos que tratam a heterocedasticidade para as variâncias condicionais na série de retornos logaritmizados (\(r_t = log(\frac{P_t}{P_{t-1}})\)) (vide modelos da família ARCH e GARCH, p. ex. aqui)
Utilizaremos aqui os preços do ativo CORN disponível no Yahoo Finances:
- CORN (Teucrium Corn Fund) \(\Rightarrow\) última cotação
2021-06-17.
Vejamos as disponibilidades de cada um deles:
library(quantmod)
CORN <- getSymbols("CORN", auto.assign = FALSE,
from = "1994-01-01", end = Sys.Date())
data_inicio <- start(CORN)
data_inicio # Mostra o primeiro registro disponivel na serie[1] "2010-06-09"data_fim <- end(CORN)
data_fim # Mostra o ultimo registro disponivel na serie[1] "2021-06-17"periodicity(CORN)Daily periodicity from 2010-06-09 to 2021-06-17 Uma breve inspeção do dataset:
library(dplyr)
glimpse(CORN)An 'xts' object on 2010-06-09/2021-06-17 containing:
Data: num [1:2776, 1:6] 25.1 25.5 25.9 26 26.2 ...
- attr(*, "dimnames")=List of 2
..$ : NULL
..$ : chr [1:6] "CORN.Open" "CORN.High" "CORN.Low" "CORN.Close" ...
Indexed by objects of class: [Date] TZ: UTC
xts Attributes:
List of 2
$ src : chr "yahoo"
$ updated: POSIXct[1:1], format: "2021-06-18 19:34:11"head(CORN) # Primeiras 5 observacoes do conjunto de dados CORN.Open CORN.High CORN.Low CORN.Close CORN.Volume CORN.Adjusted
2010-06-09 25.12 25.25 25.12 25.15 1700 25.15
2010-06-10 25.46 25.46 25.46 25.46 200 25.46
2010-06-11 25.88 25.88 25.79 25.79 500 25.79
2010-06-14 25.99 26.11 25.99 26.11 2200 26.11
2010-06-15 26.24 26.24 25.97 25.97 7000 25.97
2010-06-16 26.26 26.44 26.20 26.32 2400 26.32tail(CORN) # Ultimas 5 observacoes do dataset CORN.Open CORN.High CORN.Low CORN.Close CORN.Volume CORN.Adjusted
2021-06-10 22.37 22.73 22.25 22.46 335800 22.46
2021-06-11 22.14 22.28 21.74 22.24 260700 22.24
2021-06-14 21.23 21.61 21.07 21.33 336800 21.33
2021-06-15 20.94 21.18 20.71 21.06 289900 21.06
2021-06-16 21.24 21.50 20.94 20.96 223500 20.96
2021-06-17 20.38 20.53 19.57 19.65 694900 19.65Como toda boa análise de séries temporais, precisamos inspecionar visualmente seu padrão:
library(dygraphs)
# Função log retornos
ret<-function(x,k=1){
return(diff(log(x),k))
}
grupo <- cbind(Cl(CORN), ret(Cl(CORN),1), Vo(CORN), ret(Vo(CORN),1))
dygraph(Cl(CORN), group = "grupo") %>% dyRangeSelector() # Grafico das cotacoes de Fechamentodygraph(ret(Cl(CORN),1), group = "grupo") %>% dyRangeSelector() # Grafico dos retornos do Fechamentodygraph(Vo(CORN), group = "grupo") %>% dyRangeSelector() # Grafico do Volume negociadodygraph(ret(Vo(CORN),1), group = "grupo") %>% dyRangeSelector() # Grefico dos retornos do Volume de negociacaoTalvez a primeira limitação do prophet consista no fato de existir a necessidade da conversão de tipo (classe) de objeto de um xts aqui apresentado para um dataframe:
library(lubridate)
library(data.table)
CORN_dt <- as.data.table(CORN)
glimpse(CORN_dt)Rows: 2,776
Columns: 7
$ index <date> 2010-06-09, 2010-06-10, 2010-06-11, 2010-06-14, 2010-06~
$ CORN.Open <dbl> 25.12, 25.46, 25.88, 25.99, 26.24, 26.26, 26.20, 26.22, ~
$ CORN.High <dbl> 25.25, 25.46, 25.88, 26.11, 26.24, 26.44, 26.20, 26.60, ~
$ CORN.Low <dbl> 25.12, 25.46, 25.79, 25.99, 25.97, 26.20, 25.82, 26.22, ~
$ CORN.Close <dbl> 25.15, 25.46, 25.79, 26.11, 25.97, 26.32, 26.08, 26.39, ~
$ CORN.Volume <dbl> 1700, 200, 500, 2200, 7000, 2400, 1600, 3100, 9500, 2870~
$ CORN.Adjusted <dbl> 25.15, 25.46, 25.79, 26.11, 25.97, 26.32, 26.08, 26.39, ~CORN_dt <- CORN_dt %>%
rename(ds = "index") %>%
mutate(ds = as.Date(ds, format = "%y/%m/%d")) %>%
as.data.frame()
glimpse(CORN_dt)Rows: 2,776
Columns: 7
$ ds <date> 2010-06-09, 2010-06-10, 2010-06-11, 2010-06-14, 2010-06~
$ CORN.Open <dbl> 25.12, 25.46, 25.88, 25.99, 26.24, 26.26, 26.20, 26.22, ~
$ CORN.High <dbl> 25.25, 25.46, 25.88, 26.11, 26.24, 26.44, 26.20, 26.60, ~
$ CORN.Low <dbl> 25.12, 25.46, 25.79, 25.99, 25.97, 26.20, 25.82, 26.22, ~
$ CORN.Close <dbl> 25.15, 25.46, 25.79, 26.11, 25.97, 26.32, 26.08, 26.39, ~
$ CORN.Volume <dbl> 1700, 200, 500, 2200, 7000, 2400, 1600, 3100, 9500, 2870~
$ CORN.Adjusted <dbl> 25.15, 25.46, 25.79, 26.11, 25.97, 26.32, 26.08, 26.39, ~Seleciono as colunas que serão necessárias para projetar, uma vez que o prophet obriga que tenhamos uma coluna nominada y e outra ds contendo as datas:
CORN <- CORN_dt %>%
select(ds, CORN.Close) %>%
mutate(ds = as.Date(ds, format = "%y/%m/%d")) %>%
rename(y = "CORN.Close")%>%
as.data.frame()
glimpse(CORN)Rows: 2,776
Columns: 2
$ ds <date> 2010-06-09, 2010-06-10, 2010-06-11, 2010-06-14, 2010-06-15, 2010-0~
$ y <dbl> 25.15, 25.46, 25.79, 26.11, 25.97, 26.32, 26.08, 26.39, 25.98, 25.6~Ajusto o modelo prophet aos dados das cotações:
library(prophet)
modelo_prophet <- prophet(CORN)
projecao_prophet_dataframe <- make_future_dataframe(modelo_prophet, periods = 365) # Proximos 12 meses
projecao_prophet <- predict(modelo_prophet, projecao_prophet_dataframe)Pode-se visualizar o ajuste aos componentes da série temporal:
prophet_plot_components(modelo_prophet, projecao_prophet)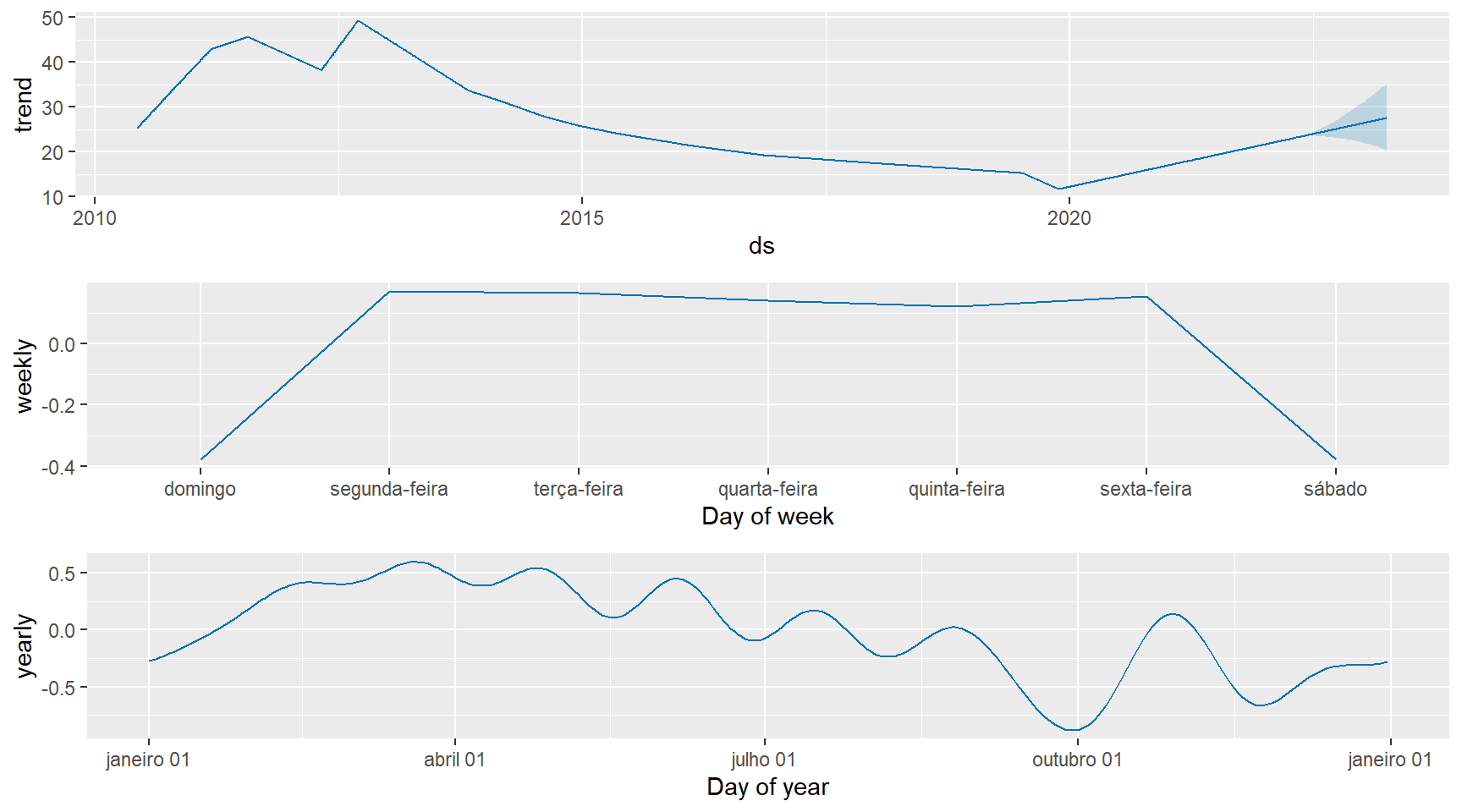
Então visualizamos essa projeção fora da amostra chamando:
library(plotly)
ggplotly(
plot(modelo_prophet, projecao_prophet) +
add_changepoints_to_plot(modelo_prophet) # Identificacao de quebras estruturais na serie
)Note que no gráfico gerado acima, o ponto de último corte/quebra estrutural pode ser utilizado como
dyplot.prophet(modelo_prophet, projecao_prophet) # Projeção dos precos do ativo CORN com prophetComo temos 16 colunas como output do prophet selecionamos somente as que precisamos comparar:
glimpse(projecao_prophet)Rows: 3,141
Columns: 19
$ ds <dttm> 2010-06-09, 2010-06-10, 2010-06-11, 2010-0~
$ trend <dbl> 25.15644, 25.22359, 25.29073, 25.49216, 25.~
$ additive_terms <dbl> 0.63249900, 0.57424150, 0.55791198, 0.44384~
$ additive_terms_lower <dbl> 0.63249900, 0.57424150, 0.55791198, 0.44384~
$ additive_terms_upper <dbl> 0.63249900, 0.57424150, 0.55791198, 0.44384~
$ weekly <dbl> 0.04172193, 0.01390618, 0.03373329, 0.05561~
$ weekly_lower <dbl> 0.04172193, 0.01390618, 0.03373329, 0.05561~
$ weekly_upper <dbl> 0.04172193, 0.01390618, 0.03373329, 0.05561~
$ yearly <dbl> 0.59077707, 0.56033533, 0.52417868, 0.38823~
$ yearly_lower <dbl> 0.59077707, 0.56033533, 0.52417868, 0.38823~
$ yearly_upper <dbl> 0.59077707, 0.56033533, 0.52417868, 0.38823~
$ multiplicative_terms <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0~
$ multiplicative_terms_lower <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0~
$ multiplicative_terms_upper <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0~
$ yhat_lower <dbl> 23.26074, 23.32490, 23.50165, 23.64840, 23.~
$ yhat_upper <dbl> 28.41974, 28.16081, 28.30121, 28.36615, 28.~
$ trend_lower <dbl> 25.15644, 25.22359, 25.29073, 25.49216, 25.~
$ trend_upper <dbl> 25.15644, 25.22359, 25.29073, 25.49216, 25.~
$ yhat <dbl> 25.78894, 25.79783, 25.84864, 25.93600, 25.~tail(projecao_prophet[c("ds", "yhat", "yhat_lower", "yhat_upper")]) ds yhat yhat_lower yhat_upper
3136 2022-06-12 16.25992 11.27749 22.21299
3137 2022-06-13 16.36941 10.98710 21.78894
3138 2022-06-14 16.31767 10.98768 22.11976
3139 2022-06-15 16.25668 10.95863 22.25329
3140 2022-06-16 16.17651 10.40291 21.98173
3141 2022-06-17 16.14334 10.65343 22.00652A validação cruzada é obtida para avaliarmos a acurácia do prophet:
val_cruzada <- cross_validation(modelo_prophet, 30, units = "days") E mais objetivamente com as medidas de ajuste:
as_tibble(performance_metrics(val_cruzada, rolling_window = 0.01)) # Para os prox 30 dias# A tibble: 30 x 8
horizon mse rmse mae mape mdape smape coverage
<drtn> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 days 3.77 1.94 1.34 0.0573 0.0375 0.0590 0.779
2 2 days 3.50 1.87 1.31 0.0556 0.0411 0.0575 0.778
3 3 days 3.44 1.85 1.33 0.0576 0.0424 0.0594 0.773
4 4 days 3.72 1.93 1.37 0.0595 0.0402 0.0610 0.749
5 5 days 4.28 2.07 1.47 0.0610 0.0421 0.0623 0.724
6 6 days 4.30 2.07 1.47 0.0609 0.0436 0.0620 0.727
7 7 days 5.07 2.25 1.59 0.0649 0.0471 0.0662 0.714
8 8 days 5.82 2.41 1.69 0.0687 0.0512 0.0705 0.692
9 9 days 5.70 2.39 1.62 0.0658 0.0416 0.0679 0.719
10 10 days 5.37 2.32 1.65 0.0680 0.0498 0.0698 0.702
# ... with 20 more rowsVeremos o gráfico da métrica de validação cruzada no horizonte projetado:
ggplotly(
plot_cross_validation_metric(val_cruzada,
metric = "smape",
rolling_window = 0.01)
)Obviamente que quanto mais longe no futuro projetarmos, maiores serão os erros de previsão.
Até aqui rodamos o script convencional do uso do prophet conforme algumas buscas ou vídeos de alguns indianos que você possa assistir no Youtube mostrando quais os comandos chamar.
Mas e se quisermos avaliar a capacidade preditiva do prophet em relação a outros métodos já conhecidos de projeção de séries temporais ?
prophet \(versus\) outros modelos de projeção de séries temporais
Como mencionado aqui, sabemos que quando falamos de projeção para fora do amostra, um futuro incerto, seja ele de curto ou longo prazo, temos a certeza da incerteza a ser considerada em nossa modelagem. Muitas críticas são feitas por renomados econometristas de que a maioria de muitos desses métodos quando empregados a problemas envolvendo dados econômicos reais pecam na sua confirmação com a realidade por serem considerados ateóricos.
O que faremos agora é um procedimento comparativo do grau de ajuste de alguns desses conhecidos modelos na série de preços do ativo em questão com a grande finalidade de avaliarmos o seu grau mínimo de erro na sua capacidade de projetar o futuro.
Tratamento inicial da série temporal financeira
Sabemos que os dias de trade não envolvem alguns feriados e finais de semana, e por este motivo faremos um tratamento desses missings em nossa série temporal. Chamaremos esses missings de gaps implícitos e faremos um tratamento na série para eles:
library(quantmod)
CORN <- getSymbols("CORN", auto.assign = FALSE,
from = "1994-01-01", end = Sys.Date())
glimpse(CORN)An 'xts' object on 2010-06-09/2021-06-17 containing:
Data: num [1:2776, 1:6] 25.1 25.5 25.9 26 26.2 ...
- attr(*, "dimnames")=List of 2
..$ : NULL
..$ : chr [1:6] "CORN.Open" "CORN.High" "CORN.Low" "CORN.Close" ...
Indexed by objects of class: [Date] TZ: UTC
xts Attributes:
List of 2
$ src : chr "yahoo"
$ updated: POSIXct[1:1], format: "2021-06-18 19:51:30"periodicity(CORN) # avalia a disponibilidade da sérieDaily periodicity from 2010-06-09 to 2021-06-17 Em seguida preciso modificar o objeto de séries temporais do R no formato xts para uma tsibble:
library(tsibble)
library(tsibbledata)
library(dplyr)
library(tidyverse)
library(data.table)
CORN <- as.data.table(CORN)
CORN <- as_tsibble(CORN)
glimpse(CORN)Rows: 2,776
Columns: 7
$ index <date> 2010-06-09, 2010-06-10, 2010-06-11, 2010-06-14, 2010-06~
$ CORN.Open <dbl> 25.12, 25.46, 25.88, 25.99, 26.24, 26.26, 26.20, 26.22, ~
$ CORN.High <dbl> 25.25, 25.46, 25.88, 26.11, 26.24, 26.44, 26.20, 26.60, ~
$ CORN.Low <dbl> 25.12, 25.46, 25.79, 25.99, 25.97, 26.20, 25.82, 26.22, ~
$ CORN.Close <dbl> 25.15, 25.46, 25.79, 26.11, 25.97, 26.32, 26.08, 26.39, ~
$ CORN.Volume <dbl> 1700, 200, 500, 2200, 7000, 2400, 1600, 3100, 9500, 2870~
$ CORN.Adjusted <dbl> 25.15, 25.46, 25.79, 26.11, 25.97, 26.32, 26.08, 26.39, ~class(CORN)[1] "tbl_ts" "tbl_df" "tbl" "data.frame"Utilizando o comando fill_gaps() droparemos os gaps implícitos repetindo nos dias faltantes a última cotação disponível.
library(tidyr)
CORN <- CORN %>%
fill_gaps() %>%
fill(c(CORN.Open, CORN.High, CORN.Low, CORN.Close, CORN.Volume, CORN.Adjusted), .direction = "down")
print(CORN)# A tsibble: 4,027 x 7 [1D]
index CORN.Open CORN.High CORN.Low CORN.Close CORN.Volume CORN.Adjusted
<date> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 2010-06-09 25.1 25.2 25.1 25.2 1700 25.2
2 2010-06-10 25.5 25.5 25.5 25.5 200 25.5
3 2010-06-11 25.9 25.9 25.8 25.8 500 25.8
4 2010-06-12 25.9 25.9 25.8 25.8 500 25.8
5 2010-06-13 25.9 25.9 25.8 25.8 500 25.8
6 2010-06-14 26.0 26.1 26.0 26.1 2200 26.1
7 2010-06-15 26.2 26.2 26.0 26.0 7000 26.0
8 2010-06-16 26.3 26.4 26.2 26.3 2400 26.3
9 2010-06-17 26.2 26.2 25.8 26.1 1600 26.1
10 2010-06-18 26.2 26.6 26.2 26.4 3100 26.4
# ... with 4,017 more rowsAgora podemos observar novamente se persistem esses gaps na série. Para isso, utilizarei ao invés do dygraph (interativo), uma visualização mais limitada com o pacote ggplot2:
library(plotly)
library(fabletools)
ggplotly(
autoplot(CORN, CORN.Close) + xlab("Tempo") + ggtitle("Cotações de fechamento do ativo CORN")
)A definição da amostra de treinamento
Este ponto é interessante de destacar, pois como nosso objetivo aqui consiste em obtermos desempenho de ajuste dos modelos in the sample, recortamos a série temporal sem considerarmos suas “quebras estruturais” (vide p. ex. teste de Chow) para tal finalidade.
Diferentemente da conhecida abordagem empregada em algoritmos de “machine learning” aqui nosso foco não é o mesmo! (conforme citação da explicação do prof. Josh Angrist feita aqui).
Selecionei a amostra de treino do seu início até 2019 com a bola de cristal apontada para os próximos 365 dias adiante.
library(fpp3)
treino <- CORN %>%
filter(year(index) <= 2019)
tail(treino) # Testo pra ver se filtrou corretamente# A tsibble: 6 x 7 [1D]
index CORN.Open CORN.High CORN.Low CORN.Close CORN.Volume CORN.Adjusted
<date> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 2019-12-26 14.8 14.8 14.8 14.8 28400 14.8
2 2019-12-27 14.8 14.9 14.8 14.9 50500 14.9
3 2019-12-28 14.8 14.9 14.8 14.9 50500 14.9
4 2019-12-29 14.8 14.9 14.8 14.9 50500 14.9
5 2019-12-30 14.8 14.9 14.8 14.8 116700 14.8
6 2019-12-31 14.9 14.9 14.8 14.8 77500 14.8Em seguida soluciono o problema dos gaps implícitos:
treino <- treino %>%
fill_gaps() %>%
fill(c(CORN.Open, CORN.High, CORN.Low, CORN.Close, CORN.Volume, CORN.Adjusted), .direction = "down")
print(treino)# A tsibble: 3,493 x 7 [1D]
index CORN.Open CORN.High CORN.Low CORN.Close CORN.Volume CORN.Adjusted
<date> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 2010-06-09 25.1 25.2 25.1 25.2 1700 25.2
2 2010-06-10 25.5 25.5 25.5 25.5 200 25.5
3 2010-06-11 25.9 25.9 25.8 25.8 500 25.8
4 2010-06-12 25.9 25.9 25.8 25.8 500 25.8
5 2010-06-13 25.9 25.9 25.8 25.8 500 25.8
6 2010-06-14 26.0 26.1 26.0 26.1 2200 26.1
7 2010-06-15 26.2 26.2 26.0 26.0 7000 26.0
8 2010-06-16 26.3 26.4 26.2 26.3 2400 26.3
9 2010-06-17 26.2 26.2 25.8 26.1 1600 26.1
10 2010-06-18 26.2 26.6 26.2 26.4 3100 26.4
# ... with 3,483 more rowsEstimação dos modelos de projeção de séries temporais
Por questões de limitação de processamento computacional, rodei somente 4 modelos diferentes para compararmos seu desempenho visual e de ajuste em relação aos dados reais. Sem detalhar muito as componentes de definição do ARIMA, ou do ETS, veremos se o prophet fica mais “bem comportado” em relação a eles:
library(fable)
library(fable.prophet)
modelos1 <- treino %>%
model(
arima = ARIMA(CORN.Close, stepwise = FALSE, approximation = FALSE), # Argumentos do ARIMA para usar uma estimativa mais lenta, mas melhor, ao selecionar a ordem do modelo
ets = ETS(CORN.Close),
prophet_aditivo = prophet(CORN.Close ~ growth("linear") + season(period = "day", order = 10) +
season(period = "week", order = 5)),
prophet_multiplicativo = prophet(CORN.Close ~ season(period = "day", order = 10,
type = "multiplicative") +
season(period = "week", order = 5,
type = "multiplicative"))
) %>%
mutate(combinadas =
(arima + ets + prophet_aditivo + prophet_multiplicativo) / 4 ) # Media aritmetica simples. Nao use a funcao mean()Agora faço a projeção com os modelos para 365 passos à frente:
ajuste_fcst_modelos1 <- modelos1 %>%
forecast(h = 365)Delimito as bandas de confiança das projeções para 95% para visualizar graficamente:
ajuste_fcst_modelos1 %>%
autoplot(CORN, level = c(95))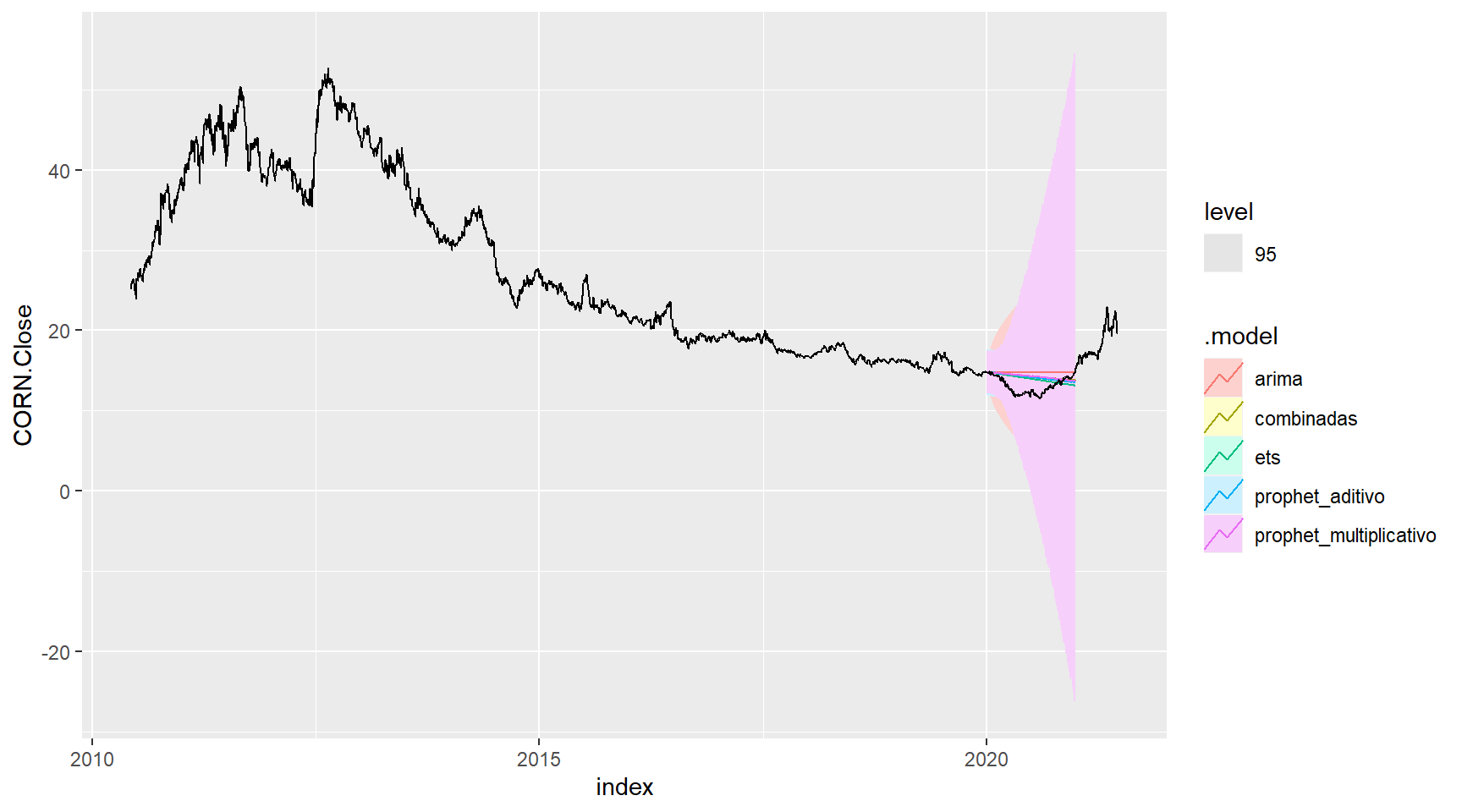
Tento fazer o mesmo para modelos diferentes para comparar novamente:
modelos2 <- treino %>%
model(
sarima = ARIMA(log(CORN.Close) ~ 0 + pdq(1,1,1) + PDQ(1,1,2)),
nntwk = NNETAR(sqrt(CORN.Close)),
prophet_aditivo = prophet(CORN.Close ~ growth("linear") + season(period = "day", order = 1) +
season(period = "week", order = 1)),
prophet_multiplicativo = prophet(CORN.Close ~ season(period = "day", order = 1,
type = "multiplicative") +
season(period = "week", order = 1,
type = "multiplicative"))
) %>%
mutate(combinadas =
(sarima + nntwk + prophet_aditivo + prophet_multiplicativo) / 4 ) # Media aritmetica simples. Nao use a funcao mean()Para 365 dias à frente:
ajuste_fcst_modelos2 <- modelos2 %>%
forecast(h = 365)Visualmente temos:
ajuste_fcst_modelos1 %>%
autoplot(CORN, level = c(95))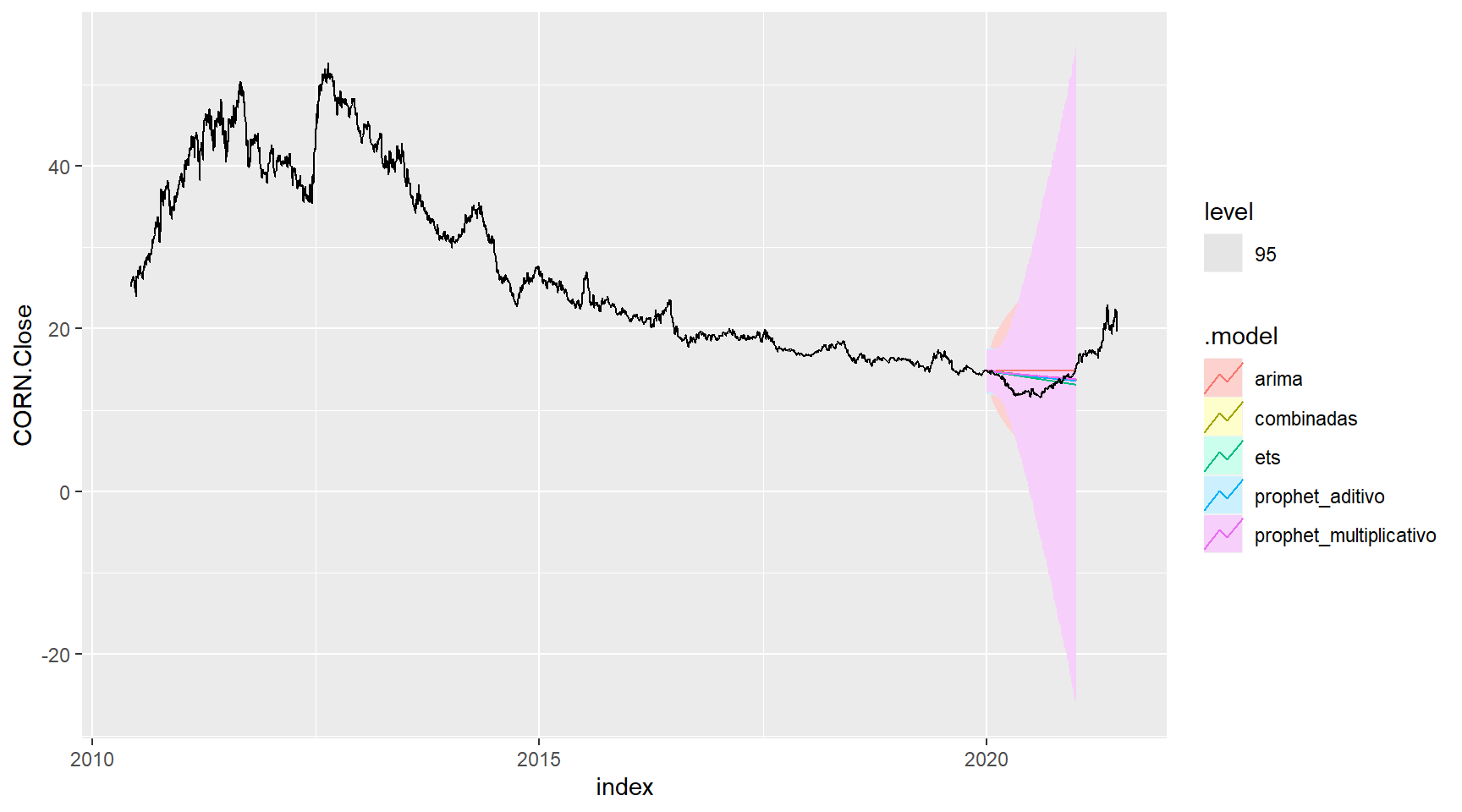
E finalmente comparamos a acurácia dos modelos contra o prophet:
ajuste_fcst_modelos1 %>%
accuracy(CORN) %>%
arrange(RMSE) # Seleção da acuracia pelo menor RMSE para o conjunto de modelos1# A tibble: 5 x 10
.model .type ME RMSE MAE MPE MAPE MASE RMSSE ACF1
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 ets Test -0.803 1.36 1.13 -6.72 9.04 1.73 1.39 0.983
2 prophet_aditivo Test -1.03 1.47 1.21 -8.47 9.67 1.83 1.50 0.982
3 combinadas Test -1.08 1.51 1.24 -8.85 9.95 1.89 1.54 0.983
4 prophet_multiplicativo Test -1.13 1.53 1.25 -9.21 10.1 1.91 1.56 0.982
5 arima Test -1.66 1.94 1.66 -13.3 13.3 2.53 1.98 0.983ajuste_fcst_modelos2 %>%
accuracy(CORN) %>%
arrange(RMSE) # Seleção da acuracia pelo menor RMSE para o conjunto de modelos2# A tibble: 5 x 10
.model .type ME RMSE MAE MPE MAPE MASE RMSSE ACF1
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 prophet_aditivo Test -1.01 1.46 1.20 -8.29 9.65 1.83 1.49 0.983
2 prophet_multiplicativo Test -1.22 1.59 1.30 -9.94 10.5 1.98 1.63 0.982
3 sarima Test -1.25 1.59 1.30 -10.1 10.5 1.98 1.63 0.982
4 combinadas Test -2.05 2.31 2.05 -16.3 16.3 3.12 2.37 0.984
5 nntwk Test -4.77 5.11 4.77 -37.2 37.2 7.25 5.22 0.989Projeção com distribuições combinadas
[continuar escrevendo…]
\[\\[1in]\]
10 erros comuns de qualquer “cientista de dados” x dados econômicos x modelagem econométrica
Além de seu professor te massacrar com uma série de derivações de provas e fórmulas matemáticas na sala de aula convencional, por mais que você não se desestimule com isso, destaco 10 erros daqueles que já trabalham com a econometria na prática:
Deixar de usar seu bom senso e conhecimento da teoria econômica
Uma das características que diferenciam a pesquisa aplicada em econometria de outras aplicações de análise estatística é o uso da teoria econômica e bom senso para motivar a conexão entre as explicativas e variáveis dependentes.
Em econometria, você deve ser capaz de fazer um caso forte para o independente variáveis (\(Xs\)) causando mudanças na variável dependente (\(Y\)). Você precisa de teoria e bom senso para justificar sua abordagem. Isso permite que você forneça uma interpretação sensata de seus resultados, além das típicas medidas de significância estatística e ajuste.
Começar com as perguntas erradas sobre o fenômeno investigado
Ficar obcecado com os detalhes técnicos da estimativa de modelos econométricos pode ser fácil. No entanto, você deve sempre dar um passo para trás e se perguntar por que você está fazendo o que está fazendo. Por que outras pessoas acharão meu tópico interessante e importante? O valor da minha variável dependente é susceptível de ser influenciado por minhas variáveis independentes no mesmo período, ou devo usar valores defasados para as variáveis independentes? Posso explicar porque algumas variáveis são lineares, outros estão em logs e alguns são polinômios? Você deveria se perguntar esses tipos de perguntas antes de estimar um modelo econométrico, vamos caminhar sozinhos antes de lidar com complicações como heteroscedasticidade e autocorrelação.
As perguntas conceituais são mais importantes do que as técnicas.
Ignorar os trabalhos e contribuições de outros econometristas
Deixar de conectar o seu trabalho com o de outras pessoas que examinaram a sua questão de pesquisa ou algo intimamente relacionado a ela é um erro grave.
Compreender como outras pessoas lidaram com questões semelhantes pode ajudá-lo a descobrir e definir qual modelo usar, pode render refinamentos em seu trabalho e permite aos leitores entenderem melhor a relevância do seu tópico.
Em sua revisão de literatura, concentre-se em artigos ou segmentos de artigos que são diretamente relacionado ao seu trabalho. Resuma a abordagem, os dados e as descobertas de outros pesquisadores. Por fim, seja claro sobre como seu trabalho se encaixa com o que já foi feito por outros, o que foi melhorado e / ou quão novo dimensões do tópico foram exploradas
Não se familiarizar com os dados
Os alunos muitas vezes presumem que os dados com os quais estão trabalhando estão completos para todas as variáveis e que as informações relatadas são precisas. Você pode reduzir suas chances de obter surpresas indesejáveis em seus resultados, fazendo alguns trabalho exploratório que inclui estatísticas descritivas, gráficos de linha (para dados de série temporal), distribuições de frequência e até mesmo listagens de alguns valores de dados individuais.
Uma série de resultados indesejáveis pode resultar da falha em se familiarizar com seus dados de análise. Esses três exemplos são talvez os mais comuns:
As variáveis que você pensava que eram medidas continuamente estão na verdade em categorias ou grupos. Por exemplo, em algumas pesquisas, os entrevistados são perguntados sobre seu nível de educação. Quando os dados são disponibilizados para pesquisadores, essas informações podem ser convertidas em anos de educação ou códigos podem ser usados para colocar indivíduos em categorias de educação (ensino médio, diploma universitário de dois anos e assim por diante). Se for o último, você precisa criar variáveis fictícias antes de prosseguir com estimativa (você pode aprender como lidar com dados categóricos e criar variáveis dummy p. ex.
As medições que você acreditava serem valores reais estão faltando na verdade (missing data). Em alguns conjuntos de dados, os valores ausentes recebem um código em vez de à esquerda em branco. Por exemplo, se uma variável mede a idade de um entrevistado, você pode ver 998 ou 999 para algumas observações. Nesse caso, 998 pode indicar o entrevistado não sabia a resposta e 999 pode indicar que ele ou ela se recusou a responder à pergunta; você precisa ler o livro de códigos de dados para encontrar o significado preciso de tais valores (se o livro de código não estiver disponível, pode ser necessário entrar em contato diretamente com o provedor de dados). Em qualquer caso, o valor deve ser tratado como ausente e recodificado como tal antes de realizar qualquer estimativa.
Os valores de dados que parecem perfeitamente legítimos são, na verdade, censurados valores. Em algumas pesquisas, a confidencialidade do entrevistado é mantida por limitar o valor de certas variáveis. Renda do entrevistado, por exemplo, pode ser “codificado no topo” em algum valor. Se a renda do entrevistado for superior o valor limite, então a resposta é simplesmente atribuída ao valor de limite.
Complicar excessivamente o(s) modelo(s); (Keep it simple, stupid)
A arte da econometria consiste em encontrar a especificação adequada ou forma funcional para modelar seu resultado específico de interesse. Em muitos casos, no entanto, a teoria pode ser vaga sobre os elementos específicos na definição e especificação do modelo.
Dada a incerteza de escolher a especificação “perfeita”, muitos econometristas cometem o erro de especificar demais seus modelos (o que significa eles incluem inúmeras variáveis irrelevantes) ou favorecem uma estimativa complicada sobre métodos e técnicas mais simples. Pode resultar em propriedades indesejáveis do estimador e dificuldade de interpretação do significado dos resultados.
Super especificação incluindo muitas variáveis irrelevantes em um modelo de regressão aumenta os erros padrão de seus coeficientes e reduz o chances de você encontrar significância estatística. Se a teoria e o bom senso não forem bastante conclusivos sobre o efeito hipotético de uma variável, é provavelmente melhor evitar incluí-lo.
O excesso de especificação também pode se manifestar com formas funcionais complicadas que não são necessárias para lidar com preocupações teóricas ou questões de dados. Algumas funções podem ser mais difíceis para interpretar e distrair os leitores do ponto principal da análise econométrica.
Consequentemente, a sofisticação adicional em seu modelo deve ser apresentada conforme necessário e não simplesmente para exibir suas habilidades econométricas.
Obsessão por medidas de melhor ajuste e significância estatística
Depois de estimar um modelo econométrico, concentre sua atenção e guie o leitor (se você estiver escrevendo um artigo de pesquisa) para os resultados que são mais relevantes para abordar sua questão de pesquisa.
A importância de seus resultados não deve ser determinada com base no ajuste (Valores de R ao quadrado) ou significância estatística sozinha. Claro, coeficientes estatisticamente insignificantes sugerem que sua variável independente provavelmente não afetará sua variável dependente. No entanto, se a falta de um relacionamento for nova ou inesperada, esta descoberta pode ser significativa! A importância de tal descoberta é que pode sugerir que a teoria econômica padrão não é válida.
A principal descoberta em muitos dos melhores artigos que usam econometria envolve resultados de insignificância estatística. Por exemplo, alguns pesquisadores descobrem que os aumentos do salário mínimo não estão relacionados a mudanças no emprego, apesar do fato de que muitos livros didáticos de microeconomia tenham usado salários mínimos como um exemplo de piso de preço como causa nas reduções no emprego.
Esquecer da significância econômica
Você pode usar medidas de significância estatística para determinar quais variáveis provavelmente não afetarão a variável dependente, mas você não pode usar para determinar quais variáveis têm um efeito relevante.
Depois de estabelecer que uma variável é estatisticamente significativa, não se esqueça para focar sua atenção no coeficiente. Às vezes, as variáveis podem ter coeficientes que são altamente estatisticamente significativos, embora não sejam econômicos a significância está associada ao resultado.
O elemento mais importante na discussão de seus resultados é a avaliação de significância estatística e magnitude para as variáveis primárias de interesse.
Se uma variável tem um coeficiente estatisticamente significativo, mas a magnitude é muito pequena para ter alguma importância, então você deve ser claro sobre a falta de importância econômica.
Supor que seus resultados sejam robustos sempre
Na maioria dos casos, a teoria econômica permite uma quantidade considerável de flexibilidade na determinação da especificação exata do modelo econométrico.
Você vai querer ver se pequenos ajustes mudam seus resultados.
Não presuma que apenas um modelo econométrico pode ser aplicado à sua pesquisa questão e que os resultados não mudarão com modificações razoáveis para sua especificação. Você deseja realizar uma análise de robustez (ou sensibilidade) para mostram que as estimativas do seu modelo não são sensíveis (são robustas) a pequenas variações nas especificações.
A validade dos seus dados, seleção de variável e especificação do modelo são todos aprimorados com verificações de robustez bem-sucedidas. Se você não puder mostrar nenhuma prova disso, os leitores terão dúvidas sobre seus resultados e conclusões.
Ser inflexível com as complexidades do mundo real
As soluções ou previsões derivadas do uso de teorias econômicas usam lógica dedução e / ou prova matemática que geralmente depende da suposição do (todas as demais constantes).
Os dados que você usa para testar hipóteses econômicas, no entanto, são derivados de um mundo onde os agentes (indivíduos, empresas ou o que você) estão envolvidos com o ambiente circundante de maneiras que não são susceptíveis de satisfazer a suposição ceteris paribus porque muitos das variáveis que definem suas circunstâncias específicas variam consideravelmente de uma observação para outro.
Não desista de uma questão de pesquisa ou conjunto de dados porque você não pode obter dados para todas as variáveis que você acha que são necessárias para testar uma hipótese. E se você aplica esse critério, nenhuma pergunta de pesquisa é apropriada e nenhum conjunto de dados sempre é bom o suficiente. Muito provavelmente, você precisará usar algumas proxies (variáveis que medem aproximadamente o que você gostaria de capturar) e usar técnicas econométricas para lidar com quaisquer problemas de estimativa.
Normalmente, os dados que você adquire não contêm todas as informações estruturadas da forma proposta pelo modelo teórico. Use proxies que parecem apropriadas e que outros considerariam aceitáveis. Além disso, evite forçar um determinado conjunto de dados em uma estimativa que não é apropriada para a questão da pesquisa - por exemplo, usando dados agregados de nível estadual quando a teoria aplica-se a indivíduos ou usando dados transversais quando um elemento de tempo é parte da sua história.
Ignorar quando encontra resultados bizarros
A maioria dos projetos de pesquisa econométrica contém resultados de estimativa para várias variações de modelos relacionados. Você quer se concentrar em suas variáveis primárias de interesse (variáveis essenciais), mas certifique-se de examinar todos os seus resultados.
Este significa não ignorar resultados irracionais (principalmente estimativas insignificantes, coeficientes com o sinal errado e magnitudes que são muito grandes) e proceder ao relatório e interpretação. Se alguns resultados não passam pelo teste do bom senso, então os testes estatísticos provavelmente não terão sentido e podem até indicar que você cometeu um erro com suas variáveis, a estimativa, técnica, ou ambos.
Aborde quaisquer problemas de estimativa que levem a resultados perversos antes de você tirar conclusões sobre seus resultados. Você deve verificar a precisão dos seu dados, a integridade das informações, a construção de suas variáveis, e a especificação do seu modelo. A correção de problemas de estimativa que são adversos pode afetar outras estimativas e também pode alterar drasticamente suas conclusões.
\[\\[1in]\]
"Havendo Deus antigamente falado muitas vezes, e de muitas maneiras, aos pais, pelos profetas, a nós falou-nos nestes últimos dias pelo Filho," Hebreus 1:1
\[\\[1in]\]
Referências
Franses, P.H. Time Series Models for Business and Economic Forecasting. Cambridge: Cambridge University Press, 1998.
R Core Team (2020). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.
Stan Development Team. YEAR. Stan Modeling Language Users Guide and Reference Manual, VERSION. https://mc-stan.org
Orloff, J., Blum, J. Comparison of frequentist and Bayesian inference, 18.05 class 20, disponível em: https://ocw.mit.edu/courses/mathematics/18-05-introduction-to-probability-and-statistics-spring-2014/readings/MIT18_05S14_Reading20.pdf, MIT, EUA, 2014.
prophet: Automatic Forecasting Procedure, disponível em: https://cran.r-project.org/web/packages/prophet/index.html
Morettin, P. Econometria Financeira: Um curso de séries temporais financeiras, 2a. ed. revista e ampliada, São Paulo, 2006.
Taylor, S., J. Forecasting at Scale, The American Statistician, 72(1), 37–45., Disponível em: https://peerj.com/preprints/3190/