Elasticidade-preço da demanda: Preço ideal para bolsas de estudos, método frequentista x bayesiano

---

Rodrigo Hermont Ozon

Econometrista/Data Scientist

Economista e mestre em Desenvolvimento Econômico pela UFPR, experiente por mais de 12 anos em sua carreira com análise de dados, modelagem, tratamento e apresentação de informações em conhecimento e tomada de decisão inteligente. Possui conhecimento em métodos estatísticos e econométricos para além dos modelos de machine learning, prefere inferência causal pois compreende que quem gera os dados são seres humanos inteligentes com decisões não automáticas e sim baseadas em princípios econômicos!

---

---

Descrição do problema

Uma plataforma de educação à distância deseja averiguar com maior clareza o perfil de seus consumidores ou alunos e durante o período compreendido entre os dias de 01 de março de 2020 até o dia 05 de junho de 2021 coletou diversas amostras de seu sistema para diferentes cursos ofertados. A primeira questão que surgiu consistiu na necessidade de avaliação de uma "reprecificação" dado a qualidade e consequente compra de seus cursos ofertados, pois a avaliação do fornecimento de bolsas integrais poderia proporcionar um maior market share e consequente maior lucratividade da empresa no futuro próximo. O econometrista do time sugeriu que trabalhassem com dados disponíveis nessa pesquisa que refletissem temporalmente os resultados dessas amostragens frente ao número de matriculados/compradores e o preço médio dos cursos vendidos naquele dia pesquisado.

• Baixe o dataset contendo os resultados amostrados para cada dia dentro do horizonte pesquisado com seu respectivo preço médio para os diferentes cursos vendidos aqui.

\[\\[1in]\]

---

Preparação dos dados da pesquisa amostrada

O resultado da pesquisa foi disponibilizado num repositório que pode ser lido diretamente “na nuvem” pelo chunk a seguir:

dataset <- read.csv(file = "https://raw.githubusercontent.com/rhozon/datasets/master/amostragens_ead.csv", head= TRUE, sep =";")

str(dataset)

'data.frame':   462 obs. of  3 variables:
 $ Periodo       : chr  "01/03/2020" "02/03/2020" "03/03/2020" "04/03/2020" ...
 $ nro_matriculas: int  1246 1231 1219 1235 1210 1213 1216 1220 1211 1232 ...
 $ preco_medio   : chr  "7189,04" "7191,7" "7193,68" "7193,72" ...

Em seguida, algumas transformações são procedidas na coluna do periodo para formato de data e na coluna de preco_medio para numérica:

library(dplyr)
library(tidyverse)
library(lubridate)

dataset <- dataset %>%
  mutate(Periodo = as.Date(Periodo, "%d/%m/%Y"),
         dia_da_semana = weekdays(Periodo),
         preco_medio = as.numeric(str_replace(preco_medio, ",", ".")))

glimpse(dataset)

Rows: 462
Columns: 4
$ Periodo        <date> 2020-03-01, 2020-03-02, 2020-03-03, 2020-03-04, 2020-03-05, 2020-03-06, 2020-03-07, 2020-03-08, 2020-03-09, 20…
$ nro_matriculas <int> 1246, 1231, 1219, 1235, 1210, 1213, 1216, 1220, 1211, 1232, 1226, 1210, 1215, 1214, 1211, 1250, 1217, 1219, 124…
$ preco_medio    <dbl> 7189.04, 7191.70, 7193.68, 7193.72, 7195.62, 7188.96, 7186.08, 7184.51, 7192.26, 7195.39, 7184.41, 7194.77, 719…
$ dia_da_semana  <chr> "domingo", "segunda-feira", "terça-feira", "quarta-feira", "quinta-feira", "sexta-feira", "sábado", "domingo", …

Brainstorm da equipe multidisciplinar de analistas do EAD

Logo, os investidores da plataforma questionaram se até qual nível de baixa de preços sem comprometimento da qualidade dos cursos oferecidos, quanto as nossas vendas mudariam ? Assim, outros questionamentos interessantes foram levantados pela equipe no brainstorm:

• O gestor de marketing pergunta: “Será que preços promocionais em determinadas épocas do ano são propulsoras de vendas e de maior ganho de mercado ?”

• Os profissionais do financeiro questionam: “O perfil de renda do público-alvo é capaz de nos fornecer pistas melhores a respeito da qualidade e quantidade de cursos vendidos ?”

• A tia do cafezinho fica curiosa: “Gente, será que as pessoas não estão mais propensas a comprar os cursos nos finais de semana ou feriados ?”

• O time de operações indaga: “Será que a qualidade alta ou baixa dos cursos oferecidos fundamenta os preços cobrados ou então é unicamente capaz de explicar um maior volume de vendas ?”

Um econometrista que participa dessa conversa com a equipe começa a pensar e tenta instigar o surgimento de alguns insights a partir destas interessantes questões debatidas e propõe o seguinte caminho rumo às repostas…

Elasticidade-preço da demanda e nível de preço ótimo

A elasticidade-preço da demanda é a relação percentual entre a variação de quantidade demanda e variação nos preços (%), ou seja, uma análise de sensibilidade sobre a razão entre as duas variáveis, que serve para medir a reação do mercado consumidor às mudanças no preço e consequentemente na função demanda por qualquer produto/serviço.

Assim, pela lei da demanda espera-se que quanto maior for o preço estabelecido para aquele bem, menor tende a ser sua procura.

As conceituações que definem os níveis de sensibilidade de qualquer bem em função de seu preço permeiam o conceito de elasticidade:

• Bens elásticos \(\rightarrow\) são aqueles que possuem elasticidade maior que 1. Ou seja, a variação na demanda é maior do que a variação no preço. Um aumento de 10% em um bem elástico, causará uma diminuição da quantidade demandada maior do que esse percentual. Alguns exemplos de bens elásticos são: café, alguns tipos de carne, calçados, roupas e, também, alguns serviços, como salão de beleza, academia, restaurantes etc. Quando o preço desses produtos ou serviços alteram, as pessoas tendem a aumentar ou reduzir o consumo

• Bens inelásticos \(\rightarrow\) com elasticidade \(<1\) são aqueles bens que quando sofrem uma variação no seu preço causam uma variação menor/pequena na quantidade demandada. Bens inelásticos são considerados bens essenciais, como medicamentos, energia, água, feijão, sal de cozinha, açúcar, etc. Quando o preço desses produtos se eleva, as pessoas não diminuem o consumo na mesma proporção. Da mesma forma, reduções no preço causam um aumento menor na quantidade demandada.

• E elasticidade unitária \(\rightarrow\) quando as variações percentuais no preço e quantidade forem iguais.

O preço é fator importante, mas não é a única variável que determina o consumo/vendagem, logo além de analisar o market share do negócio é preciso relacionar outras variáveis:

• Quais são os produtos substitutos? Se a resposta for prontamente obtida, esses produtos tem a tendência de ter demanda elástica.

• É um bem supérfluo? Nesses casos a demanda tende a ser mais elástica;

• Um bem necessário? Esses geralmente apresentam tendência menos elástica em relação ao preço, exatamente pela necessidade de consumo e não escolha (remédios)

• Qual o nível de impacto da matéria prima no custo ? Se não existe repasse de preço a receita cai e o custo aumenta, a empresa tem margem para permanecer no lucro?

• Se a empresa repassa o aumento do custo, ela perde market share?

• Trata-se de um produto durável? Se for a demanda é mais elástica em relação ao preço, ou seja, quanto maior o preço menor a demanda. Além de ser necessário nesse caso contar com a varável de substituição do bem por outro mais moderno, com outra tecnologia, ou apenas pela valorização.

Ademais outras questões precisam ser verificadas como p. ex. :

• Qual é o público-alvo e nível de renda dos consumidores ?

• Qual são suas preferências ? Existem grupos mais propensos a pagar valores maiores para diferentes padrões de qualidade nos cursos oferecidos ?

• Existe um monitoramento dos níveis de preço e demanda dos bens substitutos e complementares ? Qual a propensão do surgimento de um produto/serviço inovador que “canibalize” meu mercado ?

• Qual é a estrutura de mercado em que estamos envolvidos ? (monopólio, concorrência perfeita, oligopólio…) A compreensão dos movimentos tomados pelos “tubarões” ou grandes players deste mercado exerce demasiada influência para os que estão na base da pirâmide ?

Modelo de elasticidade-preço da demanda proposto para preço ótimo (abordagem frequentista)

Obviamente, nem todos os dados que fossem capazes de arranhar a superfície para obtenção de todas essas respostas para as perguntas levantadas acima estarão disponíveis facilmente numa situação real (a menos que a empresa disponha de uma boa grana pra comprar uma pesquisa primária para obtenção precisa desses dados, hehehe), e tendo isso em mente, considerando as restrições orçamentárias da empresa que detinha uma pesquisa amostral feita com muito esmero pela equipe de marketing do EAD atendido, o econometrista consultor, propõe que estimemos a elasticidade-preço da demanda para esse experimento com os dados que estão disponíveis para tal finalidade, mesmo sabendo que a ausência de informações relacionadas ao nível de qualidade dos cursos oferecidos e eventual dados referentes a faixa de renda dos compradores não estejam presente diretamente nos dados da pesquisa amostrada.

Como no conjunto de dados extraído da pesquisa temos somente duas variáveis de interesse em que essa relação possa ser estabelecida, uma primeira análise nos conduz a uma inspeção visual:

library(plotly)
library(ggplot2)

ggplotly(
ggplot(dataset, aes(x = Periodo, y = nro_matriculas, group = preco_medio, fill = dia_da_semana ))+
  geom_point()+
  ggtitle("Número de matrículas compradas nos cursos oferecidos no EAD")
)

Ao selecionar p. ex. um sábado ou um domingo podemos visualizar o volume de vendas de cursos nos finais de semana e se a pergunta da tia do cafezinho pode ser minimamente respondida.

Ao avaliarmos cada uma das variáveis em relação ao tempo,

library(tseries)
library(fpp2)
library(forecast)

dataset_ts <- ts(dataset, start = c(2000, 1), end = c(2021, 6), frequency = 7)

ggplotly(
autoplot(dataset_ts[,c("nro_matriculas","preco_medio")], facets=TRUE) +
  xlab("Período") + ylab("") +
  ggtitle("Fluxo de matrículas por nível de preço médio cobrado nos diferentes cursos")
)

percebemos nitidamente uma relação inversa entre a escalada de preços e o volume de cursos comprados/alunos matriculados. Ou seja, a lei da demanda se faz presente nos dados da pesquisa amostral em questão, sugerindo a possibilidade de busca de insights a respeito da sensibilidade dos clientes/consumidores aos níveis de preços dos cursos até então.

Qual seria um preço estimado ótimo para assegurar ganho de market share, sem comprometer a qualidade do serviço, mantendo a estrutura atual de custos(nível de esforço) constante ?

Então uma estimativa de um modelo log-linear que busque responder qual o impacto das variações nos preços explicados pelo número de matriculados é apresentada: (consulte o apêndice¹ para maiores esclarecimentos metodológicos a respeito.

Estimativa do modelo de elasticidade-preço da demanda na abordagem frequentista

Um modelo que considera os efeitos do tempo na análise é incluído e expresso da seguinte forma:

\[ ln(\mbox{nro_matriculas})_{t} = \alpha + \beta_{2}ln(\mbox{preco_medio})_{t}+u_{t} \]

library(broom)
library(broom.mixed)

elasticidade_preco_demanda <- lm(log(nro_matriculas) ~ log(preco_medio), data = dataset)

summary(elasticidade_preco_demanda)

Call:
lm(formula = log(nro_matriculas) ~ log(preco_medio), data = dataset)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.047039 -0.009372  0.004294  0.012283  0.031878 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)      21.36880    0.19098  111.89   <2e-16 ***
log(preco_medio) -1.60461    0.02135  -75.17   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.01753 on 460 degrees of freedom
Multiple R-squared:  0.9247,    Adjusted R-squared:  0.9246 
F-statistic:  5650 on 1 and 460 DF,  p-value: < 2.2e-16

tidy(elasticidade_preco_demanda)

# A tibble: 2 × 5
  term             estimate std.error statistic   p.value
  <chr>               <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)         21.4     0.191      112.  0        
2 log(preco_medio)    -1.60    0.0213     -75.2 1.70e-260

Como esses resultados sugerem, a elasticidade da quantidade de matriculados em relação aos preços médios cobrados por cada curso (distintos) é de cerca de -1.605, indicand que quando os preços médios aumentam em 1% as matrículas nos diversos cursos oferecidos diminuem em cerca de -1.605%, em média. As decisões de compra pelos cursos oferecidos são muito sensíveis a variações nas médias dos preços por eles cobrados.

Graficamente podemos representar a relação encontrada entre o preço médio dos cursos ofertados e a quantidade demandada por eles:

library(ggpmisc)

ggplotly(
ggplot(dataset, aes(x = log(preco_medio), y = log(nro_matriculas)))+
  geom_point()+
  stat_poly_eq(formula = y ~x,
               eq.with.lhs = "italic(hat(y))~`=`~",
               aes(label = paste(..eq.label.., ..rr.label.., sep = "*plain(\",\")~")), 
               parse = TRUE) + 
  geom_smooth(method = "lm", se = TRUE, formula = y ~ x)+
  ggtitle("Estimativa da elasticidade-preço da demanda por diferentes cursos no EAD")
)

O valor da estatística \(R^{2}\) foi de 92.47% que é uma medida de quão bem as variáveis independentes no modelo são capazes de prever a variável dependente. Isso nos demonstra que cerca de 92.47% das variações nos preços médios cobrados pelos diferentes cursos oferecidos são capazes de explicar as oscilações no número de matrículas.

Especificamente, a estatística \(R^{2}\) mede a proporção da variância na variável dependente que pode ser explicada pelas variáveis independentes. Tal como acontece com todas as proporções, o \(R^{2}\) varia de 0 a 1, com 0 representando nenhuma variância explicada e 1 representando toda a variância explicada, ou um modelo determinístico. Por causa disso, o \(R^{2}\) também é conhecido como coeficiente de determinação.

Projeção frequentista construída para possibilidade de bolsa e seu impacto em número de matrículas

Assim, se os coeficientes/parâmetros forem realmente confiáveis, poderíamos estimar o caso de bolsistas integrais para os diferentes cursos oferecidos:

\[ \mbox{demanda_bolsas_integrais} = \alpha + \beta_{2}\times 0 = \alpha \]

demanda_bolsas_integrais <- summary(elasticidade_preco_demanda)$coef[1,1] + summary(elasticidade_preco_demanda)$coef[2,1]*0
paste(round(demanda_bolsas_integrais,2),"%")

[1] "21.37 %"

Note que se isentarmos completamente o aluno da qualquer valor a ser pago pelo curso escolhido, o modelo estimado nos conduz a concluir que em média o número de matrículas subiria na ordem dos 21.37%. Ou seja, se no próximo mês projetássemos uma trajetória conforme os valores de média compreendida para o número de matriculados nos dias 01/06/2021 a 05/06/2021 atingíramos o valor de 963 \(\times\) 21.37 % \(\times\) 963 \(\approx\) 1169 matrículas para o(s) dia(s) subsequente(s).

Se fizéssemos alguma promoção relâmpago cobrando somente R$ 1 por curso, então teríamos um fluxo de matriculados na ordem de:

demanda_bolsas_promocionais <- summary(elasticidade_preco_demanda)$coef[1,1] + summary(elasticidade_preco_demanda)$coef[2,1]*1
paste(round(demanda_bolsas_promocionais,2),"%")

[1] "19.76 %"

Cobrando somente 1 real pela média dos cursos (portando 1 real por curso/aluno) teríamos então uma previsão de matriculados na casa dos 19.76% a mais em média. Assim para o início do mês de julho de 2021 com um número médio de 963 matriculas teríamos cerca de 963 \(\times\) 19.76 % \(\times\) 963 \(\approx\) 1154 matrículas para o(s) dia(s) subsequente(s), o que ligeiramente menor do que o aumento no número de matrículas dos que obterão bolsa integral.

O comando tidy() mostra a estimativa, o erro padrão, a estatística de teste e o valor \(p\) de cada coeficiente do modelo. Usando um valor de corte para \(p\) de 0,05, vemos que o número de matrículas é um preditor significativo dos níveis médios de preços. No entanto, lembre-se do que o valor \(p\) realmente nos diz.

"Ele mede quão compatíveis os seus dados são com a Hipótese nula. Qual é a probabilidade do efeito observado nos seus dados amostrais se a hipótese nula for verdadeira? Valores-P altos: seus dados são prováveis com uma hipótese nula verdadeira. Valores-P baixos: seus dados não são prováveis com uma hipótese nula verdadeira. Um valor-P baixo sugere que sua amostra fornece evidências suficientes de que você pode rejeitar a Hipótese nula para toda a população."

(Blog do Minitab)

Isso apenas nos diz a probabilidade de observar dados que dão origem a uma estatística de teste tão grande se o valor verdadeiro do parâmetro for zero.

"um valor-P é a probabilidade de obter um efeito pelo menos tão extremo quanto aquele em seus dados amostrais, assumindo que a hipótese nula é verdadeira."

(Blog do Minitab)

Este é o principal problema da regressão frequentista.

O econometrista deseja testar se realmente esses parâmetros estimados do modelo de elasticidade-preço da demanda pelos cursos são realmente significativos do ponto de vista estatístico.

Regressão bayesiana da estimativa da elasticidade-preço da demanda por cursos do EAD

Assim, se quisermos fazer inferências sobre os valores reais dos parâmetros, os valores \(p\) e a regressão frequentista falham. A estimativa bayesiana é uma solução para este problema. Com os métodos bayesianos, a probabilidade usada para regressão frequentista e o que é conhecida como priori forma uma distribuição a posteriori.

O ponto principal é que os métodos bayesianos são amostrados dessa distribuição subsequente e podemos, então, criar resumos das distribuições para fazer inferências de parâmetros. O uso dos resumos (summary) nos permite fazer inferências sobre quais valores os parâmetros podem assumir.

Voltamos a estimar nosso modelo de elasticidade-preço da demanda na abordagem de inferência bayesiana

library(rstanarm)

elasticidade_preco_demanda_bayesiana <- stan_glm(log(nro_matriculas) ~ log(preco_medio), data = dataset)

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 2.9e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.29 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.138 seconds (Warm-up)
Chain 1:                0.113 seconds (Sampling)
Chain 1:                0.251 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 1.2e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.12 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 0.113 seconds (Warm-up)
Chain 2:                0.135 seconds (Sampling)
Chain 2:                0.248 seconds (Total)
Chain 2: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3: 
Chain 3: Gradient evaluation took 1.5e-05 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.15 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3: 
Chain 3: 
Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 3: 
Chain 3:  Elapsed Time: 0.115 seconds (Warm-up)
Chain 3:                0.139 seconds (Sampling)
Chain 3:                0.254 seconds (Total)
Chain 3: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4: 
Chain 4: Gradient evaluation took 1e-05 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4: 
Chain 4: 
Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 4: 
Chain 4:  Elapsed Time: 0.138 seconds (Warm-up)
Chain 4:                0.116 seconds (Sampling)
Chain 4:                0.254 seconds (Total)
Chain 4: 

summary(elasticidade_preco_demanda_bayesiana)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      log(nro_matriculas) ~ log(preco_medio)
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 462
 predictors:   2

Estimates:
                   mean   sd   10%   50%   90%
(Intercept)      21.4    0.2 21.1  21.4  21.6 
log(preco_medio) -1.6    0.0 -1.6  -1.6  -1.6 
sigma             0.0    0.0  0.0   0.0   0.0 

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 7.0    0.0  7.0   7.0   7.0  

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                 mcse Rhat n_eff
(Intercept)      0.0  1.0  1720 
log(preco_medio) 0.0  1.0  1719 
sigma            0.0  1.0  1458 
mean_PPD         0.0  1.0  4263 
log-posterior    0.0  1.0  1182 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

tidy(elasticidade_preco_demanda_bayesiana) # Versao pormenorizada do output do modelo de regressao bayesiana

# A tibble: 2 × 3
  term             estimate std.error
  <chr>               <dbl>     <dbl>
1 (Intercept)         21.4     0.194 
2 log(preco_medio)    -1.60    0.0217

Podemos comparar os coeficientes do modelo frequentista com o bayesiano para a elasticidade-preço da demanda por cursos no EAD e notaremos praticamente os mesmos resultados. Ou seja, para a mesma estimativa via MQO para o modelo log-linear das elasticidades temos:

tidy(elasticidade_preco_demanda) # Modelo frequentista para a elasticidade-preco da demanda

# A tibble: 2 × 5
  term             estimate std.error statistic   p.value
  <chr>               <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)         21.4     0.191      112.  0        
2 log(preco_medio)    -1.60    0.0213     -75.2 1.70e-260

tidy(elasticidade_preco_demanda_bayesiana) # Modelo bayesiano estimado para os coeficientes de elasticidade-preco da demanda

# A tibble: 2 × 3
  term             estimate std.error
  <chr>               <dbl>     <dbl>
1 (Intercept)         21.4     0.194 
2 log(preco_medio)    -1.60    0.0217

Observe que as estimativas de parâmetro do modelo bayesiano não têm mais estatísticas de teste e valores de \(p\) como na regressão frequentista.

Isso ocorre porque a estimativa bayesiana mostra a distribuição a posteriori. Isso significa que, em vez de uma estimativa pontual e uma estatística de teste, obtemos uma distribuição de valores plausíveis para os parâmetros, e a seção de estimativas (demonstrada no output completo apresentado acima) resume essas distribuições. Especificamente, obtemos a média, o desvio padrão e os percentis comumente usados. Enfim, a saída do modelo bayesiano não contém estatísticas de teste ou valores \(p\).

Isso representa a diferença fundamental entre frequentistas e bayesianos. Em suma, os frequentistas assumem que os parâmetros do modelo são fixos e os dados são aleatórios, enquanto os bayesianos assumem que os dados são fixos e os parâmetros do modelo são aleatórios. Isso pode ser visto na interpretação de um valor \(p\).

Como explicado anteriomente, o valor \(p\) é a probabilidade de observar dados que dão origem a uma estatística de teste tão grande, se a hipótese nula for verdadeira. Em outras palavras, dado um conjunto de valores de parâmetros verdadeiros (a hipótese nula), qual é a probabilidade de observar um conjunto de dados aleatórios que resulta em uma estatística de teste tão grande.

Em contraste, o modelo bayesiano assume que os dados coletados são fixos e, em vez disso, há uma distribuição de possíveis valores de parâmetros que dão origem aos dados. Dito de outra forma, os bayesianos estão interessados em determinar a faixa de valores dos parâmetros que dariam origem ao seu conjunto de dados observado.

No entanto, muitas vezes é desejável ter um método para avaliar se um parâmetro estimado usando métodos bayesianos é ou não significativo. Para isso, usaremos intervalos confiáveis. Um intervalo confiável será muito semelhante a um intervalo de confiança. Um intervalo de confiança nos informa a probabilidade de que um intervalo contenha o valor verdadeiro. No entanto, o intervalo de confiança não pode nos dizer nada sobre a probabilidade de quaisquer valores específicos para o parâmetro de interesse.

Isso pode parecer complicado, mas é uma distinção importante a ser feita para ter certeza de que estamos fazendo as inferências corretas. Em contraste, os intervalos confiáveis nos dizem quais são os valores prováveis. Isso nos permite fazer inferências sobre os valores reais dos parâmetros, ao invés dos limites dos intervalos.

posterior_interval(elasticidade_preco_demanda_bayesiana, prob = 0.95) # Intervalo confiavel de 95%

                        2.5%       97.5%
(Intercept)      20.97968015 21.75119779
log(preco_medio) -1.64744585 -1.56117858
sigma             0.01648571  0.01872428

confint(elasticidade_preco_demanda, parm = "log(preco_medio)", level = 0.95) # intervalo de confiança de 95%

                     2.5 %    97.5 %
log(preco_medio) -1.646565 -1.562664

Esses intervalos são muito semelhantes ao intervalo de confiança correspondente. Aqui está o intervalo de confiança de 95% para o parâmetro log(preco_medio) em nosso modelo frequentista. Isso nos diz que há 95% de chance de que o intervalo de -1,65 a -1,56 contenha o valor verdadeiro.

Mas estamos interessados na probabilidade de o valor cair entre dois pontos, não na probabilidade de os dois pontos capturarem o valor verdadeiro. É isso que o intervalo confiável nos dá. Como você pode ver, esses intervalos fornecem intervalos muito semelhantes. Muitas vezes, pode ser o caso, mas as inferências são muito diferentes. No cenário bayesiano, podemos perguntar qual é a probabilidade de que o parâmetro esteja entre 0,60 e 0,65, e vemos uma chance de 31% de o valor verdadeiro estar nessa faixa. Como faríamos algo semelhante com intervalos de confiança de um modelo frequentista? Não podemos. Apenas os métodos bayesianos nos permitem fazer inferências sobre os valores reais do parâmetro.

A dúvida em relação ao comparativo de ajuste do modelo frequentista contra o modelo bayesiano de regressão das elasticidades preço da demanda recai sobre seu nível de acurácia/previsibilidade/ajuste. Comparando os valores de \(R^2\) para ambos os modelos obtemos:

ss_res <- var(residuals(elasticidade_preco_demanda_bayesiana))
ss_total <- var(fitted(elasticidade_preco_demanda_bayesiana)) + var(residuals(elasticidade_preco_demanda_bayesiana))
R_quad <- 1 - (ss_res / ss_total)

paste(round(R_quad*100,2),"%") # R^2 modelo bayesiano

[1] "92.47 %"

Mas como podemos obter uma estimativa da distribuição de \(R^2\) a posteriori para verificar com maior precisão seu real valor ?

r2_posteriori <- bayes_R2(elasticidade_preco_demanda_bayesiana)
summary(r2_posteriori)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 0.9033  0.9208  0.9243  0.9240  0.9276  0.9397 

Podemos então olhar para um resumo (summary()) para ter uma ideia da distribuição ou criar um intervalo de 95% de confiança (intervalo confiável) usando a função quantile.

quantile(r2_posteriori, probs = c(0.025, 0.975))

     2.5%     97.5% 
0.9133408 0.9332978 

Também podemos fazer um histograma dos valores de \(R^2\). A partir disso, podemos ver que o verdadeiro \(R^2\) do nosso modelo está provavelmente em algum lugar entre 0,905 e 0,94.

hist(r2_posteriori)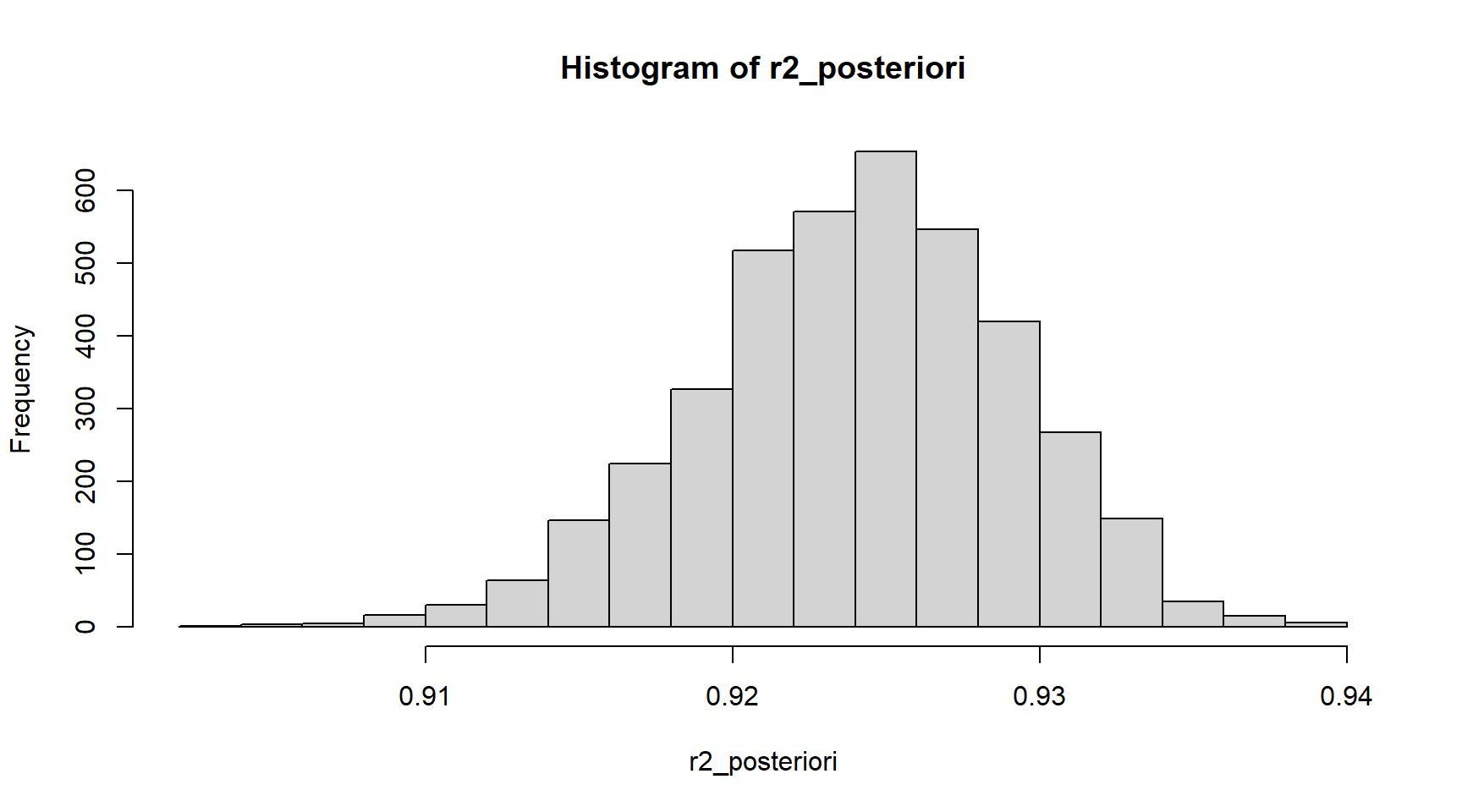

Também podemos comparar as distribuições de todas as replicações aos dados observados de uma só vez usando a função pp_check e especificando uma sobreposição de densidade. Isso irá gerar um gráfico como este:

pp_check(elasticidade_preco_demanda_bayesiana, "stat")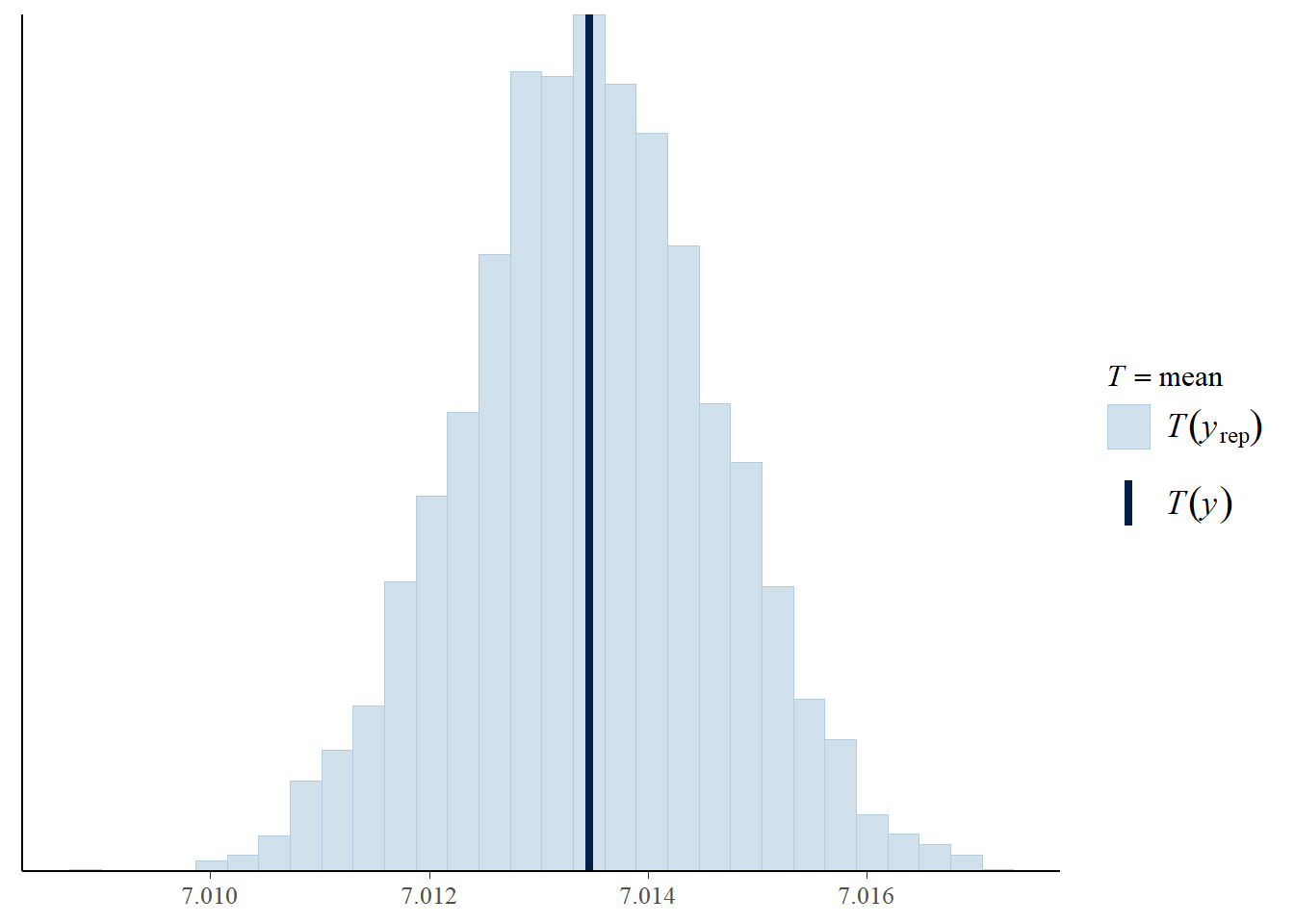

Aqui, cada linha azul clara representa a distribuição das matrículas previstas de uma única replicação e a linha azul escura representa os dados observados. Se o modelo se ajustar, a linha azul escura deve ficar alinhada com as linhas azuis claras.

Nas barras azul claras, as médias de cada replicação são representadas no histograma. A média dos dados observados é então traçada no topo como uma barra azul escura. Em nosso exemplo, a média observada do número de matrículas está dentro da faixa esperada de médias das previsões posteriores. Portanto, temos evidências de que nosso modelo se encaixa.

Podemos avaliar a densidade de matrículas previstas de replicação em comparação com a densidade observada na abordagem bayesiana:

pp_check(elasticidade_preco_demanda_bayesiana, "dens_overlay")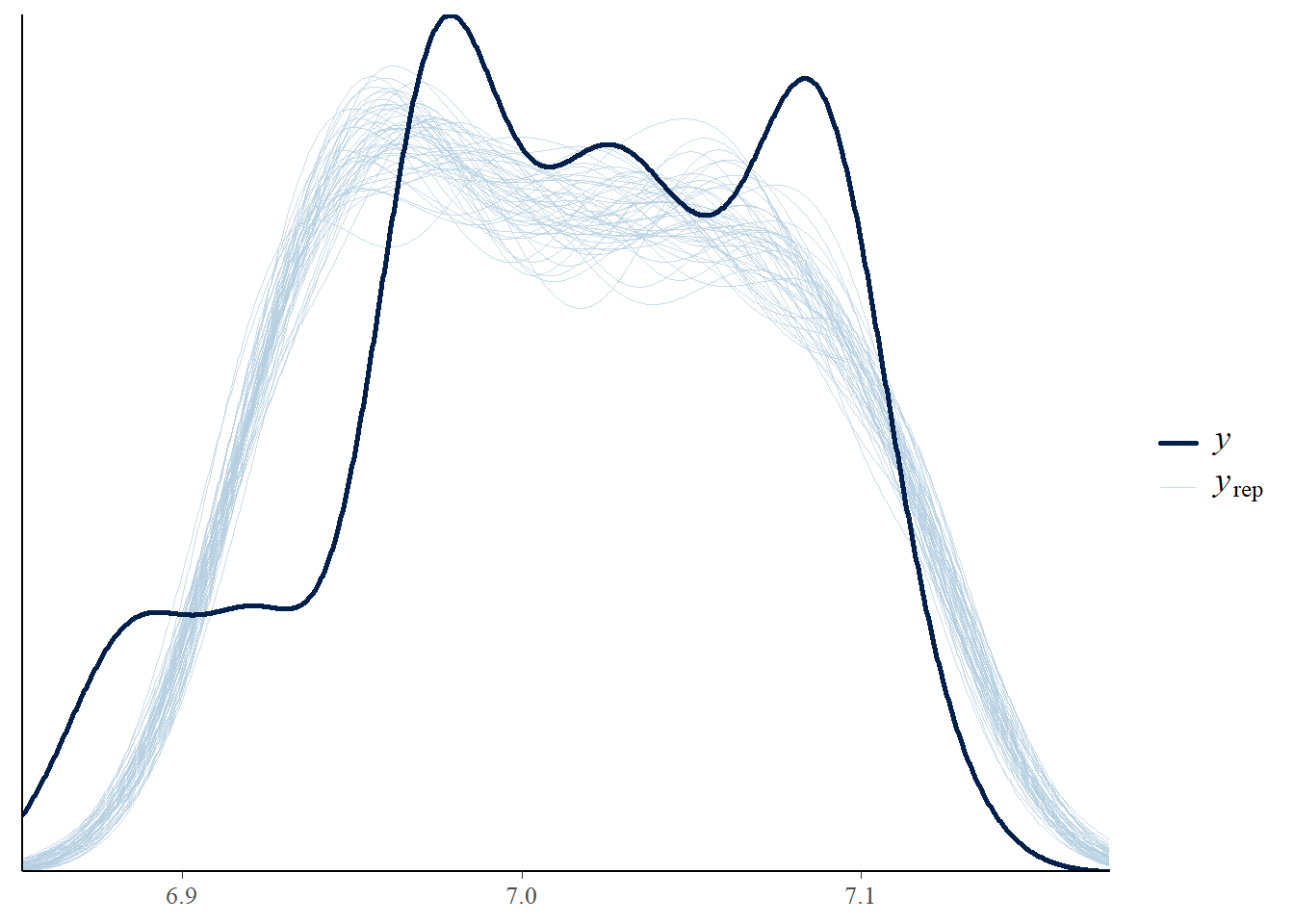

No entanto, a média é apenas um aspecto dos dados observados. Alterando “stat” para “stat_2d”, podemos observar vários aspectos de nossa variável dependente: a média e o desvio padrão.

pp_check(elasticidade_preco_demanda_bayesiana, "stat_2d")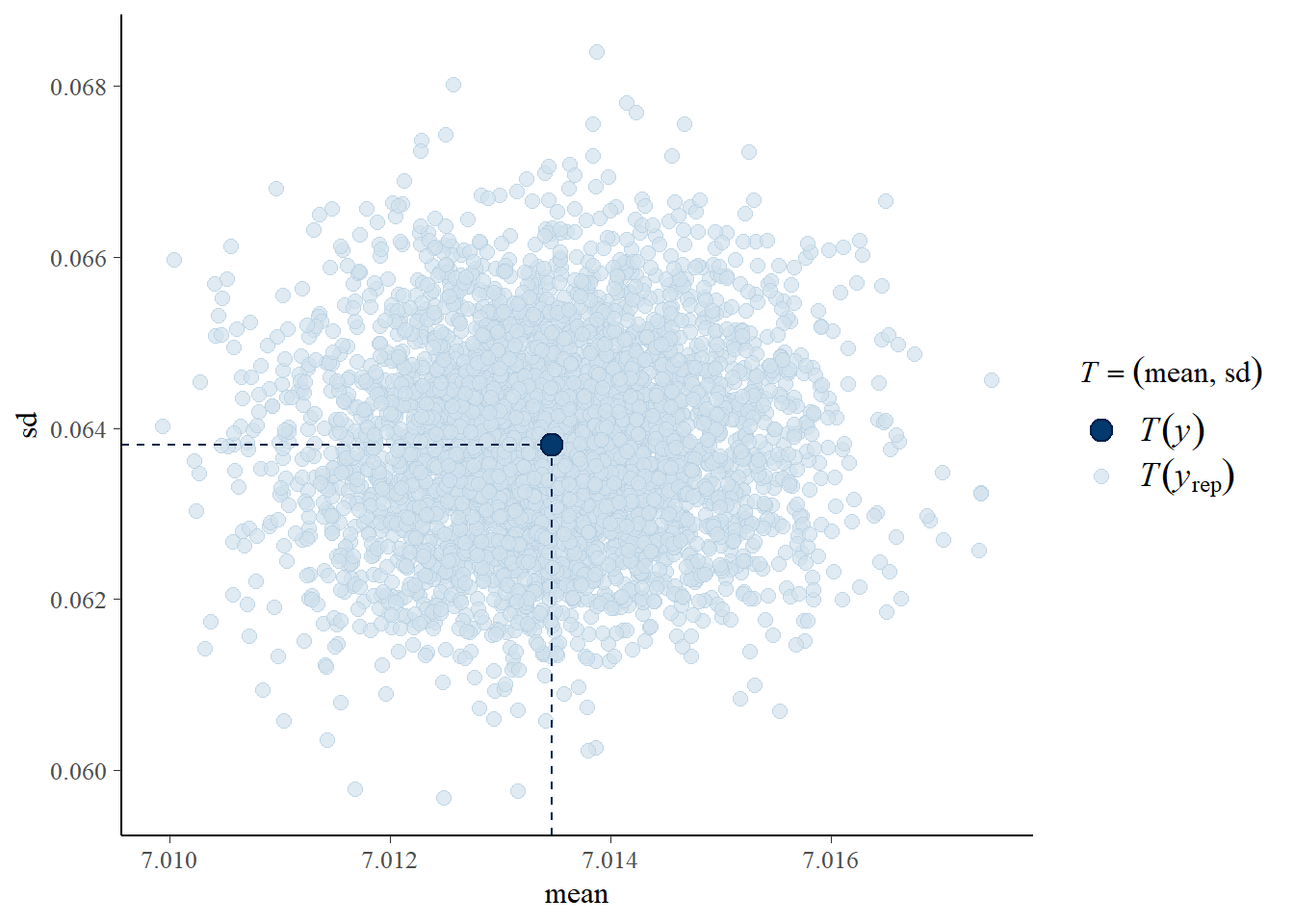

Neste gráfico, cada ponto azul claro representa a média e o desvio padrão do número de matrículas previstas em uma replicação. O ponto azul escuro mostra nossos dados observados. Como o ponto azul escuro está dentro da massa de pontos azuis claros, temos mais evidências de que nosso modelo se ajusta aos nossos dados.

Construindo projeções com o modelo bayesiano para a elasticidade-preço da demanda para novas matrículas

Veremos como podemos usar nosso modelo bayesiano estimado para fazer previsões para observações em nosso conjunto de dados e para novos dados.

posterioris <- posterior_predict(elasticidade_preco_demanda_bayesiana)
posterioris[1:10, 1:5]

             1        2        3        4        5
 [1,] 7.139528 7.083614 7.112517 7.136813 7.101321
 [2,] 7.093242 7.101655 7.108176 7.093217 7.145512
 [3,] 7.111803 7.124779 7.118190 7.123751 7.113748
 [4,] 7.077357 7.136604 7.098497 7.097079 7.147635
 [5,] 7.134511 7.156186 7.126430 7.154837 7.103334
 [6,] 7.138158 7.109537 7.114769 7.116557 7.141131
 [7,] 7.130730 7.114132 7.131489 7.127704 7.098748
 [8,] 7.091140 7.130765 7.077888 7.109876 7.099810
 [9,] 7.102147 7.120698 7.120957 7.123168 7.129919
[10,] 7.110762 7.090350 7.122967 7.124191 7.116983

Podemos então obter um números de matrículas previstas em cada iteração do modelo para cada grupo de potenciais alunos usando a função posterior_predict. Isso retorna uma matriz que possui uma linha para cada iteração e uma coluna para cada observação. Isso significa que podemos obter uma distribuição a posteriori das matrículas previstas para cada grupo de alunos.

Para fazer previsões para novos dados, primeiro temos que criar os dados que queremos prever.

predict_data <- data.frame(nro_matriculas = 1169, preco_medio = c(1, 8226.892))

predict_data

  nro_matriculas preco_medio
1           1169       1.000
2           1169    8226.892

Para este exemplo, predizemos o caso de dois grupos de alunos cujo o número estimado de matrículas nos diferentes cursos gire em torno de 1169 inscritos, considerando que um grupo será o dos bolsistas, que pagarão o irrisório valor de R$ 1 e outro não. Assim como feito anteriormente com as previsões feitas para o modelo na versão frequentista, aqui consideramos os mesmos valores da média amostral compreendida entre os dias 01 a 05/jun/2021.

Para essas previsões, criamos um novo dataframe com os mesmos nomes de variáveis de nossos dados observados. Nosso dataframe então tem duas colunas, uma para cada preditor em nosso modelo e duas linhas, uma para cada predição que queremos fazer.

Depois de criar os novos dados para previsões, podemos fornecer esse dataframe para o argumento newdata da função posterior_predict.

novas_projecoes <- posterior_predict(elasticidade_preco_demanda_bayesiana, newdata = predict_data)

Veremos os percentuais adicionais de matriculas prevista para os primeiros 10 desenhos da distribuição posteriori

novas_projecoes[1:10,]

             1        2
 [1,] 21.19188 6.966320
 [2,] 21.10094 6.910789
 [3,] 21.36777 6.893769
 [4,] 21.44104 6.898669
 [5,] 21.42854 6.902827
 [6,] 21.61404 6.892473
 [7,] 21.60556 6.892085
 [8,] 21.34067 6.889869
 [9,] 21.30810 6.910355
[10,] 21.53435 6.899584

Isso cria previsões para os novos dados em todos os 4.000 retiradas das distribuições posteriores. Aqui podemos ver as matrículas previstas para essas observações nas primeiras 10 iterações.

summary(novas_projecoes[, 1]) # Coluna de preços promocionais (1 real)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  20.70   21.23   21.36   21.37   21.50   22.08 

summary(novas_projecoes[, 2]) # Coluna de precos de mercado

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  6.848   6.891   6.903   6.903   6.915   6.989 

Olhando para os resumos, vemos que as matrículas previstas para as observações com preço promocional são consistentemente mais altas.

Para que criemos visualizações para as previsões de novos dados, seremos capazes de comunicar efetivamente a saída de nosso modelo no contexto de dados fora da amostra. Assim, visualizaremos as distribuições dessas projeções.

O primeiro passo é formatar os dados, assim como fizemos antes:

novas_projecoes[1:10,]

             1        2
 [1,] 21.19188 6.966320
 [2,] 21.10094 6.910789
 [3,] 21.36777 6.893769
 [4,] 21.44104 6.898669
 [5,] 21.42854 6.902827
 [6,] 21.61404 6.892473
 [7,] 21.60556 6.892085
 [8,] 21.34067 6.889869
 [9,] 21.30810 6.910355
[10,] 21.53435 6.899584

O primeiro passo é formatar os dados para que possamos plotá-los com ggplot2. Para fazer isso, primeiro converteremos nossas previsões subsequentes em um dataframe usando a função as.data.frame.

novas_projecoes <- as.data.frame(novas_projecoes)

Em seguida, definimos os nomes das colunas como “promocional” e “Não promocional” para que possamos identificar qual predição está em cada coluna.

colnames(novas_projecoes) <- c("Promocional", "Nao_promocional")
glimpse(novas_projecoes)

Rows: 4,000
Columns: 2
$ Promocional     <dbl> 21.19188, 21.10094, 21.36777, 21.44104, 21.42854, 21.61404, 21.60556, 21.34067, 21.30810, 21.53435, 21.34254, …
$ Nao_promocional <dbl> 6.966320, 6.910789, 6.893769, 6.898669, 6.902827, 6.892473, 6.892085, 6.889869, 6.910355, 6.899584, 6.916471, …

ggplotly(
ggplot(novas_projecoes, aes(x=Promocional)) + 
 geom_histogram(aes(y=..density..), colour="black", fill="white")+
 geom_density(alpha=.2, fill="#FF6666")+
ggtitle("Histograma e densidade da distribuição a posteriori do grupo Promocional")  
)

ggplotly(
ggplot(novas_projecoes, aes(x=Nao_promocional)) + 
 geom_histogram(aes(y=..density..), colour="black", fill="white")+
 geom_density(alpha=.2, fill="#FF6666")+
ggtitle("Histograma e densidade da distribuição a posteriori do grupo Não-promocional")  
)

Com esta visualização, podemos ver como a demanda é fortemente afetada pelos preços praticados pelos cursos ofertados no EAD. A distribuição para cursos oferecidos com valor de R$ 1 é deslocada um pouco mais para a direita, indicando um volume de matriculados mais alto. No entanto, na maioria das vezes, essas distribuições são muito semelhantes.

Isso também é consistente com o que vimos anteriormente ao examinar os resumos numéricos das distribuições. Nesses resumos, a média era consideravelmente mais alta quando o valor cobrado pela média dos cursos ficava em R$ 1,00. Assim, essas visualizações nos fornecem outra ferramenta para ajudar a comunicar as previsões feitas por nosso modelo.

Últimas considerações

Este post buscou demonstrar alguns conceitos breves e muitas vezes neglicenciado pela maioria dos "cientistas" de dados, uma vez que a natureza geradora de suas origens permeiam o "homo economicus". Neste sentido, a decisão de comprar, de vender e até mesmo de "pesquisar preços" induz potenciais consumidores e ofertantes a se readaptarem a essa nova "jornada dos dados". O prof. Joshua Angrist, do MIT enfatiza com muita veemência de que a econometria é sim a verdadeira ciência de dados, pois busca responder com uma lógica econômica questões causais muito mais fundamentais e relevantes do que simplesmente saber escrever alguns scripts em qualquer linguagem de programação. Qualquer lançamento de serviço educacional na era da informação e comunicação precisa ser adaptável e dinâmico para um novo modelo que emerge na inovação da educação e na aquisição de conhecimento na humanidade. A decisão do estabelecimento de um nível de preços, dada uma qualidade oferecida, dentro de uma estrutura de custos e nicho de público-alvo bem estabelecida precisa sempre ser capaz de capturar uma gama de dados que reflitam com acurácia os gostos e preferências de seus potenciais consumidores, níveis de renda e até mesmo os padrões de inovação e de evolução da estrutura de mercado em que se está inserido Simulamos aqui dados de quantidade de matriculados em cursos de diferentes áreas do conhecimento oferecidos remotamente (online) com diferentes políticas de preços: bolsa integral (grátis), valor irrisório e valor completo; com o objetivo de responder à questão econômica elementar de que nível de preços ótimo se deva praticar afim de manter constante o ganho de mercado e aceitação de público-alvo e saúde financeira com a estrutura de custos constante. Utilizamos a abordagem frequentista contra a abordagem bayesiana para inferirmos a respeito dos parâmetros obtidos por um modelo log-linear de elasticidade-preço da demanda com as projeções dos três cenários desenhados. Os resultados obtidos para captura dos níveis de incerteza presente no modelo de estimação se mostrou mais coerente com a realidade quando empregamos a abordagem bayesiana para tal finalidade, demonstrando o "elástico" nível demanda dos potenciais compradores para cursos oferecidos ao irrisório preço de R$ 1,00, o que parece ser um praticamente grátis com a garantia de incutir na cabeça do potencial comprador de um curso sem a bolsa o potencial significativo de ganho de market share do ead em questão. Nos resumimos a não entrar no rigor dos formalismos da matemática dos cálculos de distribuição das _posterioris_ e das aproximações LOO, e do mesmo modo de como escolher a melhor distribuição _a priori_ e as causas dos erros de estimativa no algoritmo de amostragem, por uma questão de parcimônia aqui, todavia, num próximo post, essa abordagem possa ser melhor explorada com maior detalhamento.

\[\\[1in]\]

---

Apêndice: Como medir a elasticidade: o modelo log-linear

Transcrito de Gujarati e Porter (p. 177-178, 2011).

Considere o seguinte modelo conhecido como modelo de regressão exponencial:

\[ Y_{i}= \beta_{1}X^{\beta_{2}}_{i}e^{u_{i}} \]

que também pode ser expresso como:

\[ lnY_{i} = ln\beta_{1}+ \beta_{2}lnX_{i}+u_{i} \] em que \(ln =\) logaritmo natural (logaritmo com base e, em que \(e = 2,718\))

Se escrevermos essa mesma equação como:

\[ lnY_{i}= \alpha+\beta_{2}lnX_{i}+u_{i} \]

em que \(\alpha = ln \beta_1\), este modelo é linear nos parâmetros \(\alpha\) e \(\beta_2\), linear nos logaritmos das variáveis \(Y\) e \(X\), e pode ser estimado mediante uma regressão de MQO. Devido a essa linearidade, tais modelos são denominados modelos log-log, duplo-log ou log-lineares.Se as hipóteses do modelo clássico de regressão linear forem atendidas, os parâmetros da equação acima podem ser estimados pelo método dos mínimos quadrados ordinários sendo:

\[ Y^{*} = \alpha + \beta_{2}X_{i}^{*}+u_{i} \]

em que e \(Y^{*} = 1n Y_i\) e \(X^{*}_{i} = 1n X_{i}\). Os estimadores de MQO \(\widehat{\alpha}\) e \(\widehat{\beta}\) obtidos serão os melhores estimadores lineares não viesados de \(\alpha\) e \(\beta_{2}\), respectivamente.

Um aspecto atraente do modelo log-log, que o tornou muito difundido nos trabalhos aplicados, é que o coeficiente angular \(\beta_2\) mede a elasticidade de \(Y\) em relação a \(X\), isto é, a variação percentual de \(Y\) correspondente a uma dada variação percentual (pequena) em \(X\).Se \(Y\) representa a quantidade demandada de um bem e \(X\) seu preço unitário, \(\beta_2\) mede a elasticidade preço da demanda, um parâmetro de considerável interesse econômico. Se a relação entre quantidade demandada e preço for como a da Figura 6.3a, a transformação log-log da Figura 6.3b mostrará a elasticidade preço estimada (-\(\beta_2\)).

Podemos observar dois aspectos especiais do modelo log-linear: ele pressupõe que o coeficiente da elasticidade entre \(Y\) e \(X\), \(\beta_2\), permaneça constante (por quê?), daí o nome alternativo modelo de elasticidade constante.Em outras palavras, como mostra a Figura 6.3b, a variação em \(ln Y\) por unidade de variação em \(ln X\) (isto é, a elasticidade, \(\beta_2\)) permanece a mesma com qualquer \(ln X\) utilizado para medir a elasticidade.

Outro aspecto desse modelo é que, embora \(\widehat{\alpha}\) e \(\widehat{\beta}_{2}\) sejam estimativas não viesadas de \(\alpha\) e \(\beta_1\), \(\beta_2\) (o parâmetro que entra no modelo original), ao ser estimado como \(\widehat{\beta}_{1} = antilog (\widehat{\alpha})\), é um estimador viesado. Contudo, na maioria dos problemas práticos, o termo de intercepto é de importância secundária e não é necessário preocupar-se em obter sua estimativa não viesada. No modelo de duas variáveis, o modo mais simples de decidir se o modelo log-linear ajusta-se aos dados é traçar o diagrama de dispersão de \(ln Y_i\) contra \(ln X_i\) e ver se os pontos aproximam-se de uma reta, como na Figura 6.3b.

\[\\[1in]\]

---

Referências

Angrist, J. Econometrics is the original data science vídeo informativo disponível no Youtube, acesse aqui.

Angist, J. and Pischke, J., S. Mostly Harmless Econometrics Princeton University, edition 1, number 8769, 2009, April. Disponível em: z-lib

Franses, P.H. Time Series Models for Business and Economic Forecasting. Cambridge: Cambridge University Press, 1998.

Gujarati, D. N., Porter, D. Econometria Básica, quinta ed. São Paulo, 2011.

Stan Development Team. YEAR. Stan Modeling Language Users Guide and Reference Manual, VERSION. https://mc-stan.org

Hansen, B. Econometrics, 11 de março de 2011, University of Wisconsin, Department of Economics. Disponível em https://www.ssc.wisc.edu/~bhansen