Gráfico de superfície 3d interativo para regressão linear múltipla
Rodrigo H. Ozon
21/09/2020
Resumo
Este tutorial demonstra como gerar um gráfico de superfície de regressão linear múltipla interativa utilizando o R. Aqui neste exemplo peguei os dados do curso “Introdução à Econometria utilizando o Excel” com o intuito de estimular os estudantes a interagirem com os dados que analisamos durante o aprendizado.
Palavras-chave: Gráfico 3D de regressão múltipla, interação, econometria, R

Preliminares (dados do exemplo)
Como vimos em nossas vídeo aulas de regressão linear múltipla, o gráfico de dispersão entre somente duas variáveis não atende com clareza quando precisamos inserir mais variáveis explicativas \(X\) em nosso modelo.
Dadas as estimativas de MQO para o modelo de regressão linear múltipla, vamos supor que precisássemos estimar o consumo de óleo para calefação em residências no inverno canadense. Vamos começar com um conjunto de dados obtido por uma amostra de 15 domicílios gerada por um projetista responsável por esta análise.
Embora pudéssemos considerar muitas variáveis, por motivo de simplificação devemos avaliar somente duas variáveis explicativas nesse caso:
\(\Rightarrow\) A temperatura atmosférica média diária (em graus Fahrenheit) durante o mês da coleta (\(X_{1}\));
\(\Rightarrow\) Quantidade de isolamento térmico da residência medida em polegadas (\(X_{2}\))
Como um gráfico tridimensional descreve com maior detalhe o comportamento da variável \(Y\) (consumo de óleo) contra as outras duas explicativas (temperatura e isolamento) temos uma primeira inspeção visual das pistas para causa e efeito:
Se você consultar o e-book, na página 58, verá esse gráfico:

Assim como no e-book, a imagem reproduzida acima, não nos permite interagir com o gráfico.
Você pode rodar esse script no RStudio caso deseje construí-lo e interagir com ele (somente no R):
#library(car)
#library(rgl)
#library(tidyverse)
#library(ggplot2)
#library(readxl)
#oleo<-read.csv(file="https://raw.githubusercontent.com/rhozon/Introdu-o-Econometria-com-Excel/master/proR.csv",head=TRUE,sep=";")
#v1<-oleo$qtdisolamento
#v2<-oleo$temperatura
#y1<-oleo$consumooleo
#scatter3d(x = v1, y = v2, z = y1)
#str(oleo)
#scatter3d(x = v1, y = v2, z = y1, groups = oleo$estilo,
# xlab = "Quantidade de Isolamento",
# ylab = "Temperatura",
# zlab = "Consumo de oleo para Calefacao")Aqui, neste breve tutorial, reproduziremos utilizando o R o passo a passo de como criamos esse tipo de gráfico, de forma interativa e plenamente capaz ilustrar as relações entre essas três variáveis.
O que é o R ?
R é um software livre para análise de dados. Foi desenvolvido em em 1996, com os professores de estatística Ross Ihaka e Robert Gentleman, da Universidade de Auckland que criaram uma nova linguagem computacional, similar a linguagem S desenvolvida por John Chambers.
Já outros o definem assim:
R é uma linguagem de programação estatística e gráfica que vem se especializando na manipulação, análise e visualização de dados, sendo atualmente considerada uma das melhores ferramentas para essa finalidade. A linguagem ainda possui como diferencial a facilidade no aprendizado, mesmo para aqueles que nunca tiveram contato anterior com programação. (Didática Tech)
Porque utilizar o R ?
O R é um software gratuito com código aberto com uma linguagem acessível;
a sua expansão de uso é exponencial entre pesquisadores, engenheiros e estatísticos;
ele se reinventa constantemente através de novas aplicações (aproximadamente 15.000 pacotes);
é totalmente flexível, permitindo desenvolver facilmente funções e pacotes para facilitar o trabalho;
possui um enorme capacidade gráfica e interage com apps de BI (Microsoft Power BI, p. ex.)
Está disponível para diferentes plataformas: Windows, Linux e Mac
Segundo o site datascienceacademy:
Uma imagem vale mais que 1000 palavras, certo? Mas apenas 10 palavras são necessárias para criar incríveis gráficos e imagens usando a linguagem R. A evolução e amadurecimento do R, tem levado grandes empresas como Oracle e Microsoft, a investirem seus bilionários recursos em pesquisa e desenvolvimento para aprimorar suas soluções analíticas utilizando o R como base. A linguagem R vem se tornando ainda o principal “idioma” de Cientistas e Analistas de Dados e está liderando a revolução proporcionada pelo Big Data Analytics.
Você pode baixar o R e o RStudio no site http://cran.r-project.org/ e o RStudio em https://rstudio.com/.
Caso você queira trabalhar com o R na nuvem, recomendo que você crie uma conta no RStudio Cloud em https://rstudio.com/products/cloud/
Carregando os dados de consumo de óleo para calefação
Carrego os dados direto do nosso repositório de datasets upado no GitHub:
# Preprocessamento dos dados ---------------------------------------------------------
oleo<-read.csv(file="https://raw.githubusercontent.com/rhozon/Introdu-o-Econometria-com-Excel/master/proR.csv",head=TRUE,sep=";")
str(oleo)## 'data.frame': 15 obs. of 4 variables:
## $ consumooleo : num 275.3 363.8 164.3 40.8 94.3 ...
## $ temperatura : int 40 27 40 73 64 34 9 8 23 63 ...
## $ qtdisolamento: int 3 3 10 6 6 6 6 10 10 3 ...
## $ estilo : int 2 4 6 7 8 10 12 0 8 10 ...Vamos observar o padrão de correlação das variáveis com um gráfico da matriz de correlação:
# Grafico da matriz de correlacao de todas as variaveis ------------------------------
library(corrplot)
M <- cor(oleo)
corrplot(M, method = "number")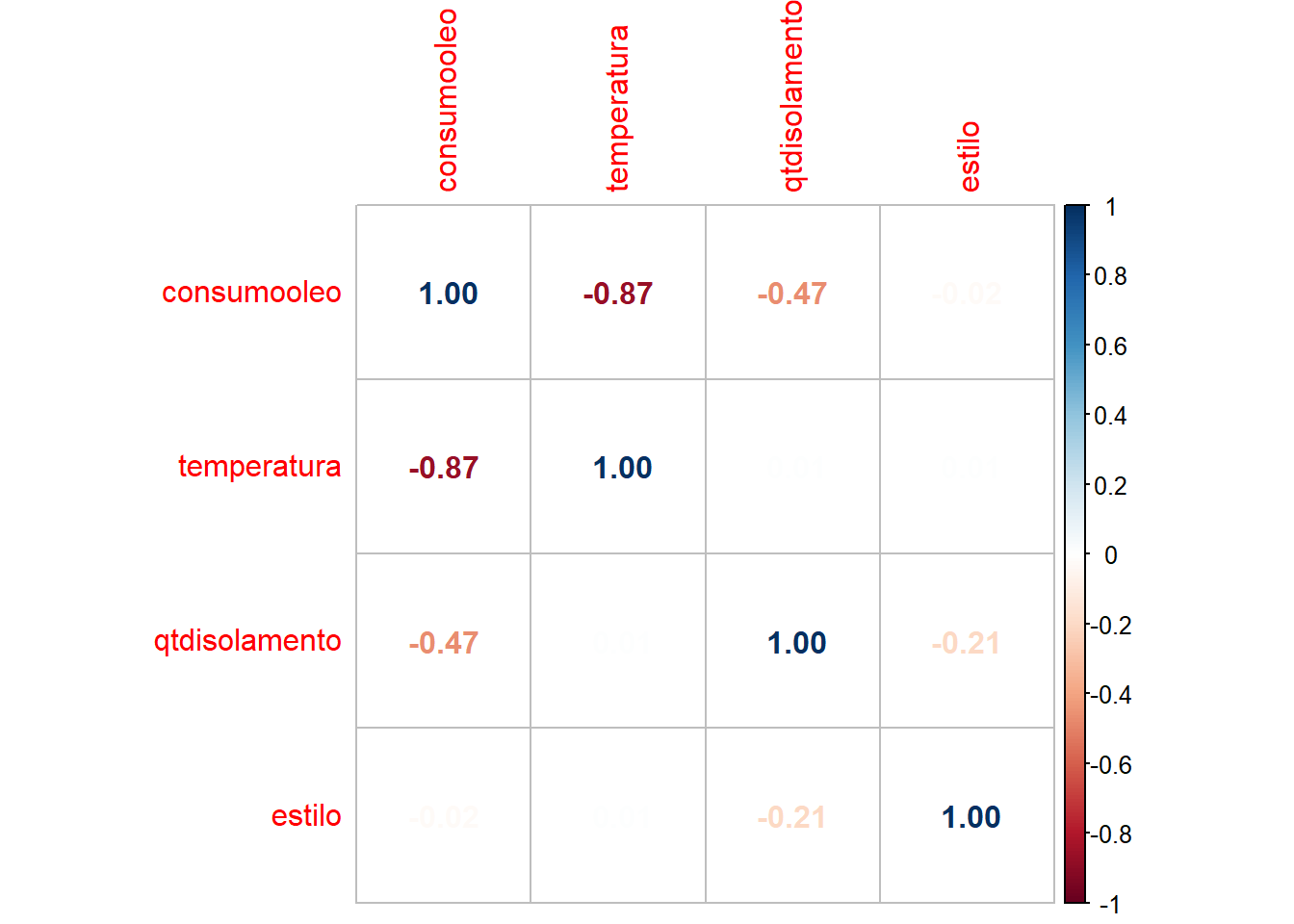
Rodando as regressões para prever o consumo de óleo para calefação
Vamos rodar os dois modelos de regressão linear múltipla com e sem a dummie de estilo das casas: (Lembre-se que “partindo de uma amostra de 15 casas, nas quais as casas de números 1, 4, 6, 7, 8, 10 e 12 são em estilo colonial”(…))
# Rodo 2 modelos de regressão simples e dois múltiplo --------------------------------
regr1 <- lm(consumooleo ~ qtdisolamento, data = oleo)
regr2 <- lm(consumooleo ~ temperatura, data = oleo)
regr3 <- lm(consumooleo ~ qtdisolamento+temperatura, data = oleo)
regr4 <- lm(consumooleo ~ qtdisolamento+temperatura+estilo, data = oleo)Assim como na função corrplot, podemos obter o coeficiente de correlação múltipla de todas as variáveis é:
# r multiplo de todas as variaveis de nosso dataset ----------------------------------
sqrt(summary(regr4)$r.squared)## [1] 0.9889055Vamos ver os resultados mais completos das regressões:
| Dependent variable: | ||||
| consumooleo | ||||
| regr1 | regr2 | regr3 | regr4 | |
| (1) | (2) | (3) | (4) | |
| Constant | 345.378*** | 436.438*** | 562.151*** | 587.248*** |
| (74.691) | (38.640) | (21.093) | (20.346) | |
| qtdisolamento | -20.350* | -20.012*** | -21.046*** | |
| (10.743) | (2.343) | (2.004) | ||
| temperatura | -5.462*** | -5.437*** | -5.430*** | |
| (0.860) | (0.336) | (0.281) | ||
| estilo | -3.324** | |||
| (1.341) | ||||
| Observations | 15 | 15 | 15 | 15 |
| R2 | 0.216 | 0.756 | 0.966 | 0.978 |
| Adjusted R2 | 0.156 | 0.738 | 0.960 | 0.972 |
| Residual Std. Error | 119.312 (df = 13) | 66.512 (df = 13) | 26.014 (df = 12) | 21.764 (df = 11) |
| F Statistic | 3.588* (df = 1; 13) | 40.377*** (df = 1; 13) | 168.471*** (df = 2; 12) | 162.503*** (df = 3; 11) |
| Note: | p<0.1; p<0.05; p<0.01 | |||
Agora vamos ver num gráfico da regressão ajustada (como se fosse no Excel), verificando cada relação entre as variáveis como estimado pelas regressões acima:
library(ggplot2)
library(lattice)
library(pdp)
require(ggiraph)
require(ggiraphExtra)
require(plyr)
a<-ggPredict(regr1,se=TRUE,interactive=TRUE)
b<-ggPredict(regr2,se=TRUE,interactive=TRUE)
c<-ggPredict(regr3,se=TRUE,interactive=TRUE)
d<-ggPredict(regr4,se=TRUE,interactive=TRUE)
a # Resultado da Regressao linear simples de Quantidade de Isolamento em Consumo de Oleob # Resultado da Regressao de Temperatura em Consumo de Oleo --------------------------c # Resultado da Regressao da Qtd Isolamento e Temperatura no Consumo de Oleo ---------d # Resultado da Regressao c com a dummie de estilo -----------------------------------Note que para os gráficos c, temos uma reta de regressão para cada nível de temperatura (em graus Fahrenheit) e no d, temos uma reta de regressão para cada estilo conforme temperatura. Perceba que os valores das inclinações não mudam, mas os valores dos interceptos sim (por quê ?).
Mas ainda assim, está um pouco difícil a nossa interpretação dessas relações entre as variáveis de nosso modelo de previsão de consumo de óleo para calefação…
Construção da superfície de regressão num gráfico 3D interativo no R
Caso você queira um script pronto adapte esse aqui
Mas, vamos utilizar um método mais simples para gerar esse gráfico.
library(plotly) # Pacote para utilizar a funcao plot_ly para graficos interativos via RMarkdown
p<-plot_ly(data = oleo, z = ~ consumooleo, x = ~ temperatura, y = ~ qtdisolamento, color=~estilo, colors = c('#0C4B8E' ,'#BF382A'),opacity = 0.5) %>%
add_markers(x = ~ temperatura,
y = ~ qtdisolamento,
z = ~ consumooleo, #No eixo z sempre coloque a variavel dependente
marker = list(size = 5),
hoverinfo = 'text',
text = ~paste(
"Consumo de Oleo para Calefacao", consumooleo, "<br>",
"Quantidade de Isolamento Termico ", qtdisolamento, "<br>",
"Temperatura atmosferica ", temperatura))
pInicialmente repassaremos a construção do gráfico acima (num outro estilo) em seguida iremos inserir uma outra superfície para representar a inclusão da dummie de estilo. Comecemos com a regressão linear múltipla de nosso modelo, para vermos os coeficientes:
mod <- lm(consumooleo ~ temperatura + qtdisolamento, data = oleo)
mod##
## Call:
## lm(formula = consumooleo ~ temperatura + qtdisolamento, data = oleo)
##
## Coefficients:
## (Intercept) temperatura qtdisolamento
## 562.151 -5.437 -20.012Primeiro, criamos um range dos pares de valores possíveis das variáveis explicativas. Esse range deve estar acima do intervalo real dos dados presentes em cada variável. Fizemos isso para armazenarmos o resultado como um objeto de dados chamado range.
range <- expand.grid(temperatura = seq(5, 90, by = 5), #valor abaixo do min e acima do max
qtdisolamento = seq(2, 15, by = 3))Agora vamos ver como as explicativas se comportam no gráfico frente a dependente:
padrao_explicativas <- ggplot(data = oleo,
aes(x = qtdisolamento, y = temperatura)) + #aqui no grafico coloquei a temperatura no eixo vertical para facilitar a visualizacao
geom_point(aes(color = consumooleo)) +
theme_bw()
ggplotly(padrao_explicativas)Agora use a função augment() para criar um data.frame que contém os valores que o modelo produz para cada linha da seu range.
estimativa <- broom::augment(mod, newdata = range)Use geom_tile para ilustrar esses valores previstos no gráfico padrao_explicativas. Use aesthetic para preenchimento e defina alpha = 0.5.
grafpreenchido<-padrao_explicativas +
geom_tile(data = estimativa, aes(fill = .fitted), alpha = 0.5)
ggplotly(grafpreenchido).fitted é o mesmo que estimado ou ajustado para onde você posicionar seu mouse no gráfico.
Agora, para definirmos um plano para a superfície da regressão, precisamos rever nosso modelo regredido (sem a dummie):
summary(mod)$coef## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 562.151009 21.0931043 26.650938 4.778685e-12
## temperatura -5.436581 0.3362162 -16.169896 1.641776e-09
## qtdisolamento -20.012321 2.3425052 -8.543127 1.907309e-06Usaremos add_surface() para desenhar um plano através da nuvem de pontos definindo z = ~ plano. Veja a Wikipedia para a definição de um produto externo de vetores veja o artigo traduzido. A seguir, usaremos a função outer() para calcular os valores do plano.
range_x <- seq(from = min(oleo$temperatura)-0.5*min(oleo$temperatura), to = max(oleo$temperatura)+0.5*max(oleo$temperatura), length = 70)# representa <min temperatura e >max temperatura
range_y <- seq(from = min(oleo$qtdisolamento)-0.5*min(oleo$qtdisolamento), to = max(oleo$qtdisolamento)+0.5*max(oleo$qtdisolamento), length = 70)# representa <min qtdisolamento e >max qtdisolamento
plano <- outer(range_x, range_y, function(a, b){summary(mod)$coef[1,1] +
summary(mod)$coef[2,1]*a + summary(mod)$coef[3,1]*b})# representa os coeficientes estimados da regressaoLembrando que esses valores para as coordenadas \(x\) e \(y\) acima descritos são as mesmas definidas em nosso range anteriormente. É interessante que saibamos que os valores desses ranges precisam cobrir abaixo e acima dos limites inferiores dos valores mínimos e máximos para as variáveis contidas neles.
Após delinearmos os valores do plano, podemos agora adicionar os valores regredidos de nosso modelo sem a dummie como uma reta superfície:
# Grafico 3D das tres variaveis e seu relacionamento----------------------------------
p<-p %>%
add_surface(x = ~range_x, y = ~range_y, z = ~plano, showscale = FALSE)%>%
# Nomes dos eixos:
layout(
title = "Grafico 3D da superficie de regressao",
scene = list(
zaxis = list(title = "Consumo de Oleo para Calefacao"),
yaxis = list(title = "Temperatura Atmosferica"),
xaxis = list(title = "Quantidade de Isolamento Termico")))Inserindo a dummie de estilo das casas
Agora que temos dois planos diferentes de superfície, inserimos o modelo completo com seus coeficientes:
modI <- lm(consumooleo ~ temperatura + qtdisolamento + estilo, data = oleo)
summary(modI)$coef## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 587.248081 20.3459359 28.863164 1.014703e-11
## temperatura -5.429520 0.2813079 -19.300990 7.825259e-10
## qtdisolamento -21.045871 2.0037138 -10.503432 4.515829e-07
## estilo -3.323923 1.3410449 -2.478607 3.064947e-02Vamos comparar os valores das regressões sem e com a dummie de estilo:
| Dependent variable: | ||
| consumooleo | ||
| mod | modI | |
| (1) | (2) | |
| Constant | 562.151*** | 587.248*** |
| (21.093) | (20.346) | |
| temperatura | -5.437*** | -5.430*** |
| (0.336) | (0.281) | |
| qtdisolamento | -20.012*** | -21.046*** |
| (2.343) | (2.004) | |
| estilo | -3.324** | |
| (1.341) | ||
| Observations | 15 | 15 |
| R2 | 0.966 | 0.978 |
| Adjusted R2 | 0.960 | 0.972 |
| Residual Std. Error | 26.014 (df = 12) | 21.764 (df = 11) |
| F Statistic | 168.471*** (df = 2; 12) | 162.503*** (df = 3; 11) |
| Note: | p<0.1; p<0.05; p<0.01 | |
Então finalmente obtemos os valores dos planos (superfícies):
# Os valores de plano (regressao mod) representados pelas retas de MQO serao utilizados como valores de superficie de curva no grafico
#plano<-outer(range_x, range_y, function(a, b){summary(mod)$coef[1,1] +
# summary(mod)$coef[2,1]*a + summary(mod)$coef[3,1]*b})
plano1<-outer(range_x, range_y,
function(a, b){summary(mod)$coef[1,1] +summary(mod)$coef[2,1]*a + summary(mod)$coef[3,1]*b + summary(modI)$coef[4,1] })Note que o objeto plano1 representa uma equação de regressão com os coeficientes de \(\widehat{\alpha}\) e \(\widehat{\beta}_{1}\mbox{temperatura}+\widehat{\beta}_{2}\mbox{qtdisolamento}\) da regressão mod, ou seja, sem a inclusão da dummie de estilo colonial das casas.
Usando finalmente a função plot_ly para desenhar o gráfico de dispersão 3D para consumooleo como uma função de temperatura, qtdisolamento e estilo mapeando a variável \(z\) para a resposta e as variáveis \(x\) e \(y\) para as variáveis explicativas. A quantidade de isolamento deve estar no eixo x e a temperatura deve estar no eixo \(y\). Use a cor para representar o estilo.
grafdummie <- plot_ly(data = oleo, z = ~consumooleo, x = ~qtdisolamento, y = ~temperatura, opacity = 0.6) %>%
add_markers(color = ~estilo)%>%
layout(
title = "Superficie de Regressao 3D",
scene = list(
zaxis = list(title = "Consumo de Oleo para Calefacao"),
yaxis = list(title = "Temperatura Atmosferica"),
xaxis = list(title = "Quantidade de Isolamento Termico")))
grafdummieEntão desenhamos os dois planos:
p %>%
add_surface(x = ~range_x, y = ~range_y, z = ~plano, showscale = FALSE) p2<-p%>%
add_surface(x = ~range_x, y = ~range_y, z = ~plano1, showscale = FALSE)
p2Quando inserimos uma curva sobre a outra, como as distâncias são extremamente pequenas fica difícil a visualização no gráfico. Note ao passar o mouse trace1 e trace2.
Exercício proposto
*Para você que já é usuário do R, fica como exercício fazer esse gráfico com a variável estilo como factor (use mutate e as.factor) para transformá-la.
Solução
oleo<-oleo%>%
mutate(estilo=as.factor(estilo))
str(oleo)## 'data.frame': 15 obs. of 4 variables:
## $ consumooleo : num 275.3 363.8 164.3 40.8 94.3 ...
## $ temperatura : int 40 27 40 73 64 34 9 8 23 63 ...
## $ qtdisolamento: int 3 3 10 6 6 6 6 10 10 3 ...
## $ estilo : Factor w/ 8 levels "0","2","4","6",..: 2 3 4 5 6 7 8 1 6 7 ...Nova regressão:
modII<-lm(consumooleo ~ temperatura + qtdisolamento + estilo, data = oleo)
summary(modII)$coef## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 604.92179 23.647895 25.58036552 1.704846e-06
## temperatura -5.35218 0.299356 -17.87898141 1.004945e-05
## qtdisolamento -23.65321 2.230118 -10.60625819 1.288231e-04
## estilo2 -44.57497 24.411853 -1.82595601 1.274289e-01
## estilo4 -25.65331 24.623981 -1.04180192 3.452334e-01
## estilo6 1.20907 17.041574 0.07094829 9.461893e-01
## estilo7 -31.49341 24.362637 -1.29269283 2.526266e-01
## estilo8 -16.82631 16.676801 -1.00896509 3.592962e-01
## estilo10 -62.75163 18.840355 -3.33070320 2.076295e-02
## estilo12 -44.09805 17.758929 -2.48314829 5.562602e-02Comparando os modelos de regressão até agora, temos:
| Dependent variable: | |||
| consumooleo | |||
| mod | modI | modII | |
| (1) | (2) | (3) | |
| Constant | 562.151*** | 587.248*** | 604.922*** |
| (21.093) | (20.346) | (23.648) | |
| temperatura | -5.437*** | -5.430*** | -5.352*** |
| (0.336) | (0.281) | (0.299) | |
| qtdisolamento | -20.012*** | -21.046*** | -23.653*** |
| (2.343) | (2.004) | (2.230) | |
| estilo | -3.324** | ||
| (1.341) | |||
| estilo2 | -44.575 | ||
| (24.412) | |||
| estilo4 | -25.653 | ||
| (24.624) | |||
| estilo6 | 1.209 | ||
| (17.042) | |||
| estilo7 | -31.493 | ||
| (24.363) | |||
| estilo8 | -16.826 | ||
| (16.677) | |||
| estilo10 | -62.752** | ||
| (18.840) | |||
| estilo12 | -44.098* | ||
| (17.759) | |||
| Observations | 15 | 15 | 15 |
| R2 | 0.966 | 0.978 | 0.992 |
| Adjusted R2 | 0.960 | 0.972 | 0.978 |
| Residual Std. Error | 26.014 (df = 12) | 21.764 (df = 11) | 19.152 (df = 5) |
| F Statistic | 168.471*** (df = 2; 12) | 162.503*** (df = 3; 11) | 70.977*** (df = 9; 5) |
| Note: | p<0.1; p<0.05; p<0.01 | ||
Repare como o valor de \(F\) reduz substancialmente neste modelo, e ainda com coeficientes sem significância estatística.
Agora com os novos valores regredidos temos:
range_x <- seq(5, 90, length = 70)#representa <min temperatura e >max temperatura
range_y <- seq(2, 15, length = 70)#representa <min qtdisolamento e >max qtdisolamento
planofator <- outer(range_x, range_y, function(a, b){summary(modII)$coef[1,1] +
summary(modII)$coef[2,1]*a + summary(modII)$coef[3,1]*b+ summary(modII)$coef[4,1]+ summary(modII)$coef[5,1]+ summary(modII)$coef[6,1]+ summary(modII)$coef[7,1]+ summary(modII)$coef[8,1]+ summary(modII)$coef[9,1]+ summary(modII)$coef[10,1]})Então inserimos na superficie:
p3<-p %>%
add_surface(x = ~range_x, y = ~range_y, z = ~planofator, showscale = FALSE)
p3Ficou estranho, pois a superfície abaixo do gráfico inicial da regressão mod, se ajustou melhor a nuvem de pontos (veja trace2 e trace1). Vamos criar a dummie com a condição sim=0 e não=1 ou simplesmente quali. Lembrando da condição que “partindo de uma amostra de 15 casas, nas quais as casas de números 1, 4, 6, 7, 8, 10 e 12 são em estilo colonial (…)”
oleo<-oleo%>%
mutate(dummie=ifelse(estilo==1,"Sim",
ifelse(estilo==4,"Sim",
ifelse(estilo==6,"Sim",
ifelse(estilo==7,"Sim",
ifelse(estilo==8,"Sim",
ifelse(estilo==10,"Sim",
ifelse(estilo==12,"Sim","Nao"))))))))
str(oleo)## 'data.frame': 15 obs. of 5 variables:
## $ consumooleo : num 275.3 363.8 164.3 40.8 94.3 ...
## $ temperatura : int 40 27 40 73 64 34 9 8 23 63 ...
## $ qtdisolamento: int 3 3 10 6 6 6 6 10 10 3 ...
## $ estilo : Factor w/ 8 levels "0","2","4","6",..: 2 3 4 5 6 7 8 1 6 7 ...
## $ dummie : chr "Nao" "Sim" "Sim" "Sim" ...Refazemos a regressão
modIII<-lm(consumooleo ~ temperatura + qtdisolamento + dummie, data = oleo)
summary(modIII)$coef## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 576.33514 23.874417 24.140282 7.041185e-11
## temperatura -5.40901 0.331129 -16.335055 4.630532e-09
## qtdisolamento -20.61794 2.356466 -8.749517 2.760504e-06
## dummieSim -17.18810 14.364639 -1.196556 2.566329e-01Então comparamos novamente os modelos:
| Dependent variable: | ||||
| consumooleo | ||||
| mod | modI | modII | modIII | |
| (1) | (2) | (3) | (4) | |
| Constant | 562.151*** | 587.248*** | 604.922*** | 576.335*** |
| (21.093) | (20.346) | (23.648) | (23.874) | |
| temperatura | -5.437*** | -5.430*** | -5.352*** | -5.409*** |
| (0.336) | (0.281) | (0.299) | (0.331) | |
| qtdisolamento | -20.012*** | -21.046*** | -23.653*** | -20.618*** |
| (2.343) | (2.004) | (2.230) | (2.356) | |
| estilo | -3.324** | |||
| (1.341) | ||||
| estilo2 | -44.575 | |||
| (24.412) | ||||
| estilo4 | -25.653 | |||
| (24.624) | ||||
| estilo6 | 1.209 | |||
| (17.042) | ||||
| estilo7 | -31.493 | |||
| (24.363) | ||||
| estilo8 | -16.826 | |||
| (16.677) | ||||
| estilo10 | -62.752** | |||
| (18.840) | ||||
| estilo12 | -44.098* | |||
| (17.759) | ||||
| dummieSim | -17.188 | |||
| (14.365) | ||||
| Observations | 15 | 15 | 15 | 15 |
| R2 | 0.966 | 0.978 | 0.992 | 0.970 |
| Adjusted R2 | 0.960 | 0.972 | 0.978 | 0.961 |
| Residual Std. Error | 26.014 (df = 12) | 21.764 (df = 11) | 19.152 (df = 5) | 25.558 (df = 11) |
| F Statistic | 168.471*** (df = 2; 12) | 162.503*** (df = 3; 11) | 70.977*** (df = 9; 5) | 116.832*** (df = 3; 11) |
| Note: | p<0.1; p<0.05; p<0.01 | |||
A nossa dummie sim e não, ainda não apresentou significância. O valor de \(F\) subiu em relação ao modelo anterior.
Agora construiremos o plano da reta para compararmos graficamente o ajuste:
planomodIII <- outer(range_x, range_y, function(a, b){summary(modIII)$coef[1,1] +
summary(modIII)$coef[2,1]*a + summary(modIII)$coef[3,1]*b+ summary(modIII)$coef[4,1]})Vamos inserir no gráfico todas as retas estimadas
p %>%
add_surface(x = ~range_x, y = ~range_y, z = ~plano1, showscale = FALSE)%>%
add_surface(x = ~range_x, y = ~range_y, z = ~planofator, showscale = FALSE)%>%
add_surface(x = ~range_x, y = ~range_y, z = ~planomodIII, showscale = FALSE) Usando os critérios de Akaike e BIC (Schwarz Bayesian Information Criterion) temos a seleção do melhor modelo
aic<-AIC(mod, modI, modII, modIII)
bic<-BIC(mod, modI, modII ,modIII)O modelo com menor valor de AIC ou BIC seria aquele de melhor ajuste.
Vamos ajustar os resultados em ordem do maior para o menor:
aic## df AIC
## mod 4 144.9798
## modI 5 140.3239
## modII 11 136.6608
## modIII 5 145.1444bic## df BIC
## mod 4 147.8120
## modI 5 143.8642
## modII 11 144.4494
## modIII 5 148.6847Note que ambos os critérios não selecionam o modelo inicial (mod) como o de melhor ajuste estatístico, mas eles escolhem o modI e modII.
Fica a pergunta, para você querido aluno…Usando qual critério você escolheria o modelo mais próximo da realidade nesse caso ? Você se orientaria pelas curvas ajustadas aos gráficos (planos ou superfícies) ou você se basearia simplesmente nos critérios de \(R^{2}\), AIC ou BIC, teste F ?
Abraços e bons estudos!
Exercício complementar
Vamos comparar o resultado de um modelo de regressão logística gaussiano para esses dados contra as regressões ajustadas anteriormente.
Utilize como exercício a função glm do R com a opção de family=gaussian(), regredindo como variável dependente o Consumo de Óleo para Calefação contra Quantidade de Isolamento Térmico + Temperatura Atmosférica + Estilo das casas.
Compare os resultados com o modelo linear (utilize BIC e AIC) e plote o gráfico tridimensional com os dois planos comparativamente.
Minha recomendação de tutorial para rodar a regressão logística é esse aqui
Referências
OZON, R. H. Introdução à Econometria com Excel, Curso interativo disponibilizado em Udemy.com, nov./2020.