Redes econômicas: Teoria de Redes na Economia usando R

---

Resumo

Segundo o professor pesquisador, José Carlos Cavalcanti, do departamento de Economia da UFPE:

“As Economias de Rede são aquelas que se originam na produção de bens e serviços de rede, e marcadamente dos bens e serviços de Tecnologias de Informação e Comunicação- TIC’s. Os mercados que incluem bens e serviços tais como telefones, e-mail, Internet, hardware de computadores, software de computadores (e de celulares, palms, PDAs-personal digital assistants), tocadores de música, vídeo players, vídeo movies, serviços bancários, serviços de aerolinhas, serviços legais, e muitos mais, são denominados de bens e serviços em rede.”

Particularmente, gostei também da definição de Jackson, p. 18, 2014:

“Economists cannot ignore that many human decisions are made in the context of, and shapped by, networks of interactions. The variety of settings in wich networks analyses are providing deep insights is already substantial and continues to expand, including: development economics, labor markets, risk sharing, local public good adoption, marketing, international trade, financial markets, and political economy. As such, it is inevitable that economic research on social networks will continue to grow and become part of an economist´s basic toolbox.

---

Introdução

Um aspecto da ciência de dados é a diversidade de tipos de dados. Normalmente os dados que nós estamos a examinar tem medidas relacionadas a uma unidade de análise - altura e peso de um pessoa, por exemplo. Em dados de rede, enfatizamos as conexões entre as unidades de análise - Fulano e Beltrano falam um com o outro?

Refletindo sobre a crescente importância do estudo das redes na economia, traduzo a contribuição de Jackson (2014, p. 3-4):

“…enquanto os economistas se esforçam para construir melhores modelos de comportamento humano, eles não podem ignorar que os humanos são fundamentalmente uma espécie social com padrões de interação que moldam seus comportamentos. … Em última análise, toda a rede de relacionamentos - quão densa é, se alguns os grupos são segregados, quem se senta em posições centrais - afeta como as informações se espalham e como as pessoas se comportam.”

O R tem um rico conjunto de pacotes para análise de rede. O pacote igraph (Csardi e Nepusz 2006) é um dos pacotes líderes. Estaremos usando os pacotes tidygraph (Pedersen 2019) e ggnetwork (Briatte 2016) aqui; ambos têm uma abordagem tidyverse (Wickham 2017) para a análise de rede. O tidygraph pacote baseia-se no pacote igraph (Csardi and Nepusz 2006). o pacote intergraph (Bojanowski 2015) é útil na conversão de objetos de rede que funcionam com pacotes diferentes na R. Por enquanto, vamos carregar o tidyverse e pacotes tidygraph.

library(tidyverse)
library(tidygraph)

A biblioteca plotly fornece interatividade aos gráficos gerados pelo pacote ggplot2 em documentos html gerados via RMarkdown:

library(plotly)

Um exemplo simples com dados criados

Começamos com um exemplo hipotético simples. Temos um conjunto de pessoas que conversam entre si. João e Maria falam um com o outro - o gráfico não é direcionado - João é o a primeira pessoa no vetor ‘de’ e Maria é a primeira pessoa no vetor ‘para’.

de <- c("João","Douglas","Maria","Paulo","Sônia","Sônia")
para <- c("Maria","Maria","Ana","Ana","Paulo","João")

Na mesma toada do pacote tidyverse do R, adicionaremos elementos de rede e criamos uma tibble chamada no1:

no1 <- tibble(de,para)
str(no1)

## tibble [6 × 2] (S3: tbl_df/tbl/data.frame)
##  $ de  : chr [1:6] "João" "Douglas" "Maria" "Paulo" ...
##  $ para: chr [1:6] "Maria" "Maria" "Ana" "Ana" ...

class(no1)

## [1] "tbl_df"     "tbl"        "data.frame"

no1

## # A tibble: 6 × 2
##   de      para 
##   <chr>   <chr>
## 1 João    Maria
## 2 Douglas Maria
## 3 Maria   Ana  
## 4 Paulo   Ana  
## 5 Sônia   Paulo
## 6 Sônia   João

A tibble no1 é uma tibble usual, ou seja, um tipo de conjunto de dados.

Os diferentes pacotes para redes no R usam objetos diferentes. Faremos uma série de operações começando com o objeto no1. Antes de passarmos para o específico código, pode ser útil fornecer uma visão geral:

1. no1 é uma tibble/dataframe. Usamos a função tbl_graph para converter isso para:

2. Fale, que é um tbl_graph. Usamos a função asNetwork para converter isto para:

3. Fale_n, que é uma rede. Usamos a função ggnetwork para converter isto para:

4. Fale_g, que é um dataframe. Observe que este dataframe tem informações que irão permitir plotagem. Usamos a função ggplot para converter isso para:

5. Fale_GG, que é um ggplot, e nos dá um gráfico do gráfico da rede.

Voltando ao no1, usamos a função tbl_graph do tidygraph pacote para convertê-lo em um objeto que armazena informações sobre nós (aqui João, Douglas etc.) e as extremidades (se uma pessoa fala com outra):

Fale <- tbl_graph(edges = no1,directed = FALSE)
Fale

## # A tbl_graph: 6 nodes and 6 edges
## #
## # An undirected simple graph with 1 component
## #
## # A tibble: 6 × 1
##   name   
##   <chr>  
## 1 João   
## 2 Maria  
## 3 Douglas
## 4 Ana    
## 5 Paulo  
## 6 Sônia  
## #
## # A tibble: 6 × 2
##    from    to
##   <int> <int>
## 1     1     2
## 2     2     3
## 3     2     4
## # ℹ 3 more rows

class(Fale)

## [1] "tbl_graph" "igraph"

Para esclarecer: tbl_graph converteu a tibble no1 no objeto Fale, que é um tbl_graph, e que tem 6 nós (João, Maria etc.) e 6 arestas (conexões entre os nós).

Usamos activate para colocar o nó ou os dados das extremidades em jogo. Vamos trazer as extremidades em jogo:

Fale %>%
activate(edges) %>%
as_tibble()

## # A tibble: 6 × 2
##    from    to
##   <int> <int>
## 1     1     2
## 2     2     3
## 3     2     4
## 4     4     5
## 5     5     6
## 6     1     6

class(Fale)

## [1] "tbl_graph" "igraph"

Compare a saída acima com a abaixo, onde os nós são ativados:

Fale %>%
activate(nodes) %>%
as_tibble()

## # A tibble: 6 × 1
##   name   
##   <chr>  
## 1 João   
## 2 Maria  
## 3 Douglas
## 4 Ana    
## 5 Paulo  
## 6 Sônia

class(Fale)

## [1] "tbl_graph" "igraph"

Agora usaremos o pacote ggnetwork para plotar nossa pequena rede. Nós precisamos para primeiro converter o objeto Talk em um objeto de rede que ggnetwork possa se referenciar. O pacote intergraph nos ajuda a converter objetos, sua função asNetwork muda o objeto Fale.

library(intergraph)
Fale_n <- asNetwork(Fale)
Fale_n

##  Network attributes:
##   vertices = 6 
##   directed = FALSE 
##   hyper = FALSE 
##   loops = FALSE 
##   multiple = FALSE 
##   bipartite = FALSE 
##   total edges= 6 
##     missing edges= 0 
##     non-missing edges= 6 
## 
##  Vertex attribute names: 
##     vertex.names 
## 
## No edge attributes

class(Fale_n)

## [1] "network"

Agora ggnetwork irá converter Fale_n em um dataframe, que tem informações o que facilitará a plotagem por ggplot:

library(ggnetwork)
Fale_g <- ggnetwork(Fale_n)
class(Fale_g)

## [1] "data.frame"

Vemos que a função ggnetwork criou um dataframe que pode ser usado para traçar a rede usando o pacote ggplot2. Alguns newgeoms — geom_edges, geom_nodes, e geom_nodetext—nos ajuda a plot os nós, extremidades e textos sobre os nós.

Fale_GG <- ggplot(Fale_g, aes(x,y, xend = xend, yend = yend)) +
                  geom_edges(color = "lightgrey") +
                  geom_nodes(alpha = 0.6, size = 5) +
                  geom_nodetext(aes(label = vertex.names),
                  col = "blue") +
                  theme_blank()

Fale_GG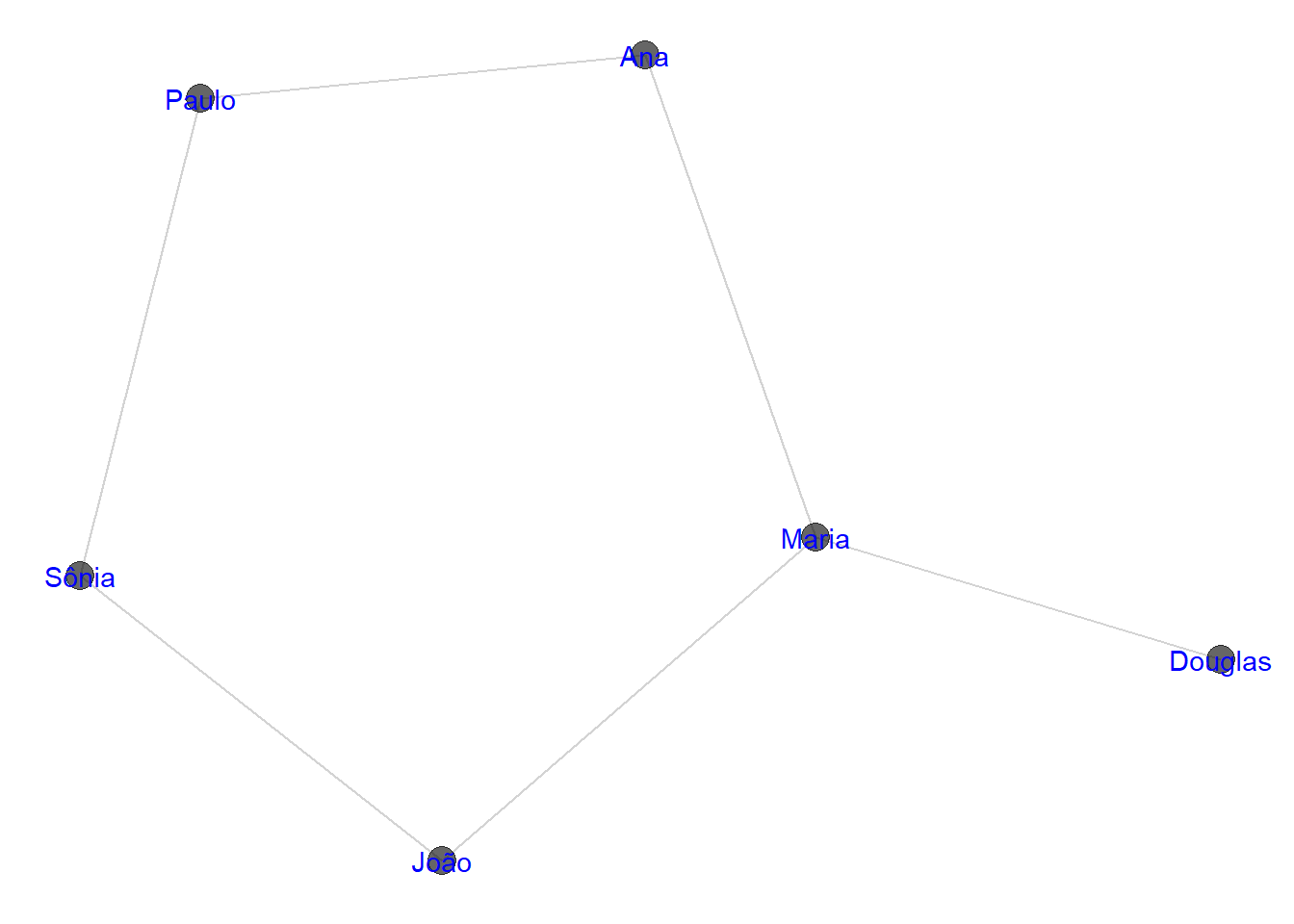

class(Fale_GG)

## [1] "gg"     "ggplot"

Nosso gráfico inicial da rede não é muito claro. Pode exigir algum esforço para obter a visualização correta das redes. Dependendo do contexto e do tamanho do gráfico, podemos usar geoms diferentes para obter um gráfico que ilumina. Nós criamos nosso própria função que podemos usar repetidamente, e que nos dá um gráfico mais claro, embora é adequado para redes que não são grandes.

ggredeplot <- function(Rede = Bali) {
Rede <- ggnetwork(Rede, layout ="kamadakawai")
ggplot(Rede, aes(x,y, xend = xend,yend = yend)) +
                geom_edges(col = "tomato") +

geom_nodetext_repel(aes(label = vertex.names),
                        col = "black", size = 3) +
theme_blank()
}

#apos criada a funcao, usamos ela pra plotar
ggredeplot(Fale_n)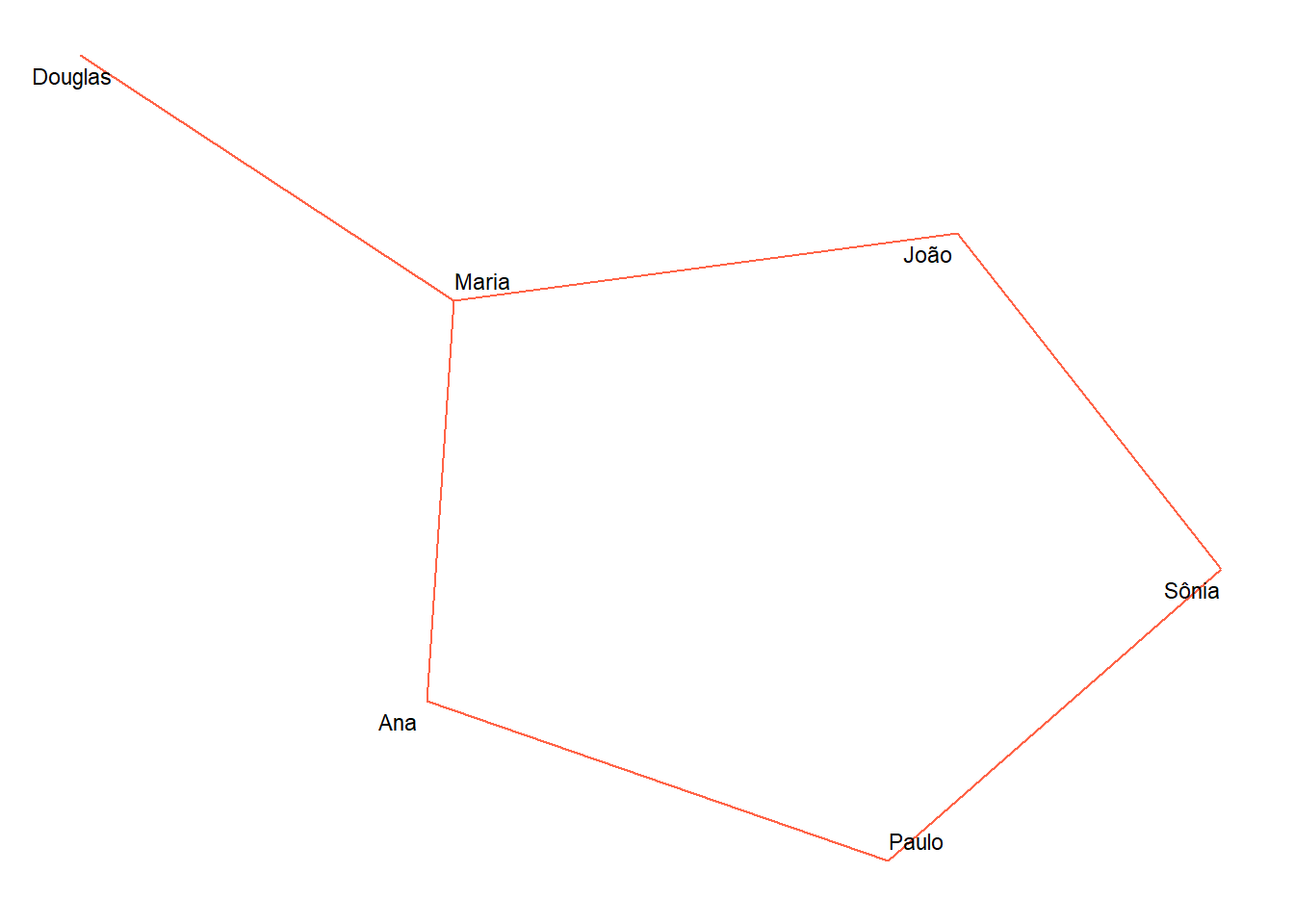

---

Exercício sugerido

Crie e plote uma pequena rede, onde Tim fala com José, Kim fala com José e Jane, e Jane fala com José. Você pode começar com:

#dica

#de <- c("Kim", "Tim", "Kim", "José")
#para <- c("José", "José", "Jane", "Jane")

A rede Medici

Agora representamos graficamente uma rede de casamentos entre famílias proeminentes em Florença, que foi pesquisado por Padgett e Ansell (1993, p. 1260), que analisou o “início Ascensão de Cosimo de ’Medici no século 15 na Florença renascentista.”

Padgett e Ansell (1993, p. 1260) enfocou “a estrutura e o surgimento sequencial do casamento, redes econômicas e de clientelismo que constituíram a política Mediceana, usada por Cosimo em 1434 para assumir o renascimento do Estado florentino.” Os dados estão no pacote netrankr (Schoch 2017).

library(netrankr)
data("florentine_m")
class(florentine_m)

## [1] "igraph"

Convertemos florentine_m em flor e depois em flor_g:

flor <- as_tbl_graph(florentine_m)
class(flor)

## [1] "tbl_graph" "igraph"

flor_g <- asNetwork(flor)
class(flor_g)

## [1] "network"

Agora traçamos a rede de casamento florentino, usando a função ggnetplot que criamos na seção anterior. Diferentes famílias são exibidas (nós), junto com seus relacionamentos por meio de casamentos.

ggredeplot(flor_g)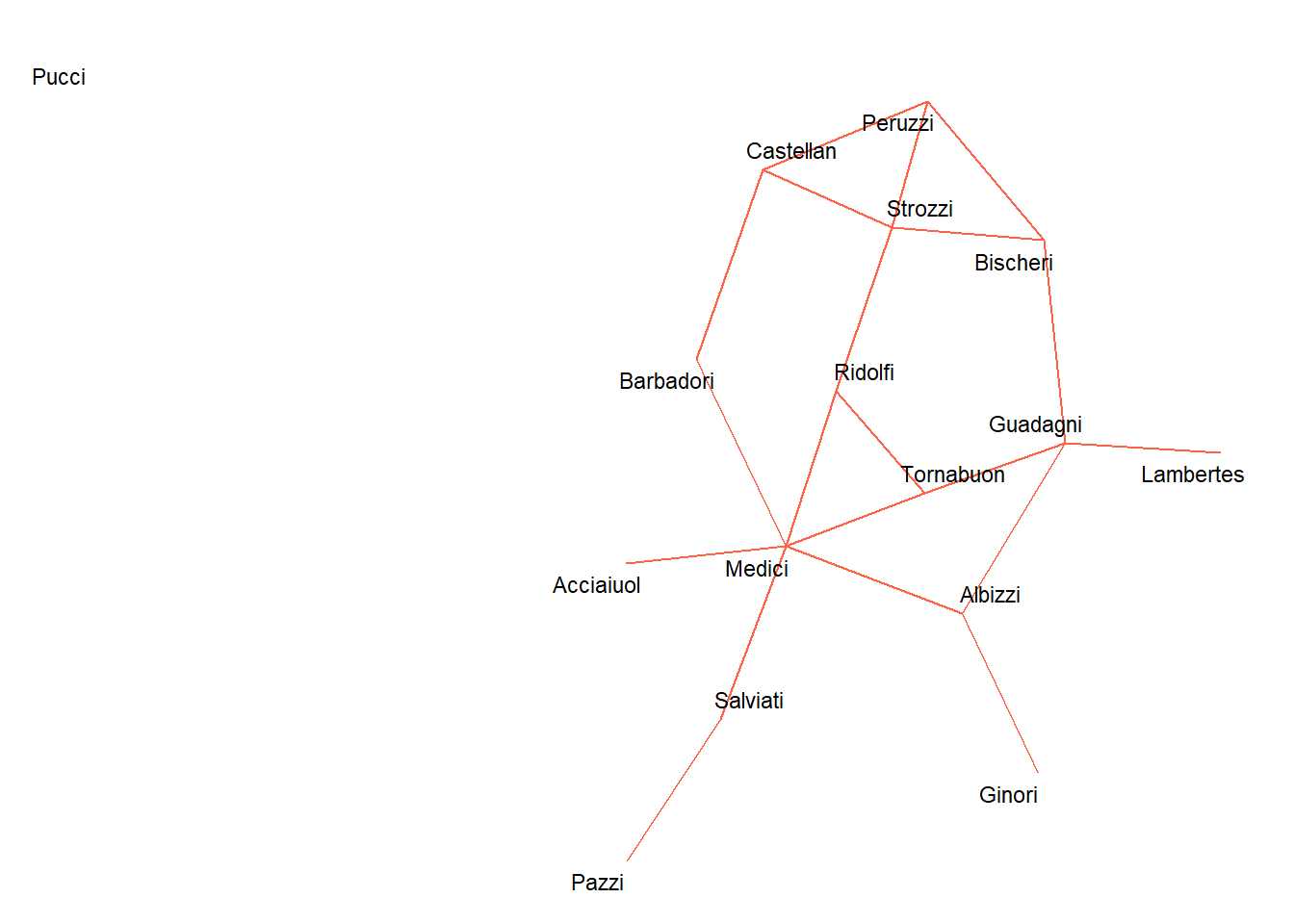

Agora calculamos um índice de centralidade, usando uma medida simples, com a função centrality_degree. Degree conta o número de arestas que sair de um determinado nó. A família Ginori tem um nó saindo dela, então grau um. Usaremos essa medida ao longo desse tutorial. Nosso código está relacionado as linhas do código tidyverse.

flor2 <- flor %>%
activate(nodes) %>%
mutate(degree = centrality_degree())

Extraímos os dados de riqueza e grau por família e organizamos os dados por grau:

flor3 <- as_tibble(flor2) %>%
arrange(-degree)
class(flor3)

## [1] "tbl_df"     "tbl"        "data.frame"

flor3

## # A tibble: 16 × 3
##    name      wealth degree
##    <chr>      <int>  <dbl>
##  1 Medici       103      6
##  2 Guadagni       8      4
##  3 Strozzi      146      4
##  4 Albizzi       36      3
##  5 Bischeri      44      3
##  6 Castellan     20      3
##  7 Peruzzi       49      3
##  8 Ridolfi       27      3
##  9 Tornabuon     48      3
## 10 Barbadori     55      2
## 11 Salviati      10      2
## 12 Acciaiuol     10      1
## 13 Ginori        32      1
## 14 Lambertes     42      1
## 15 Pazzi         48      1
## 16 Pucci          3      0

Podemos plotar a relação entre riqueza e grau usando o objeto flor3 que criamos acima. Usamos o pacote ggrepel (Slowikowski 2019) para obter rótulos legais e organizados.

library(ggrepel)
grafflor3<-ggplot(flor3, aes(x= wealth, y = degree, label = name)) +
                  geom_point() +
# posiciona os nomes adequadamente
                  geom_text_repel()

grafflor3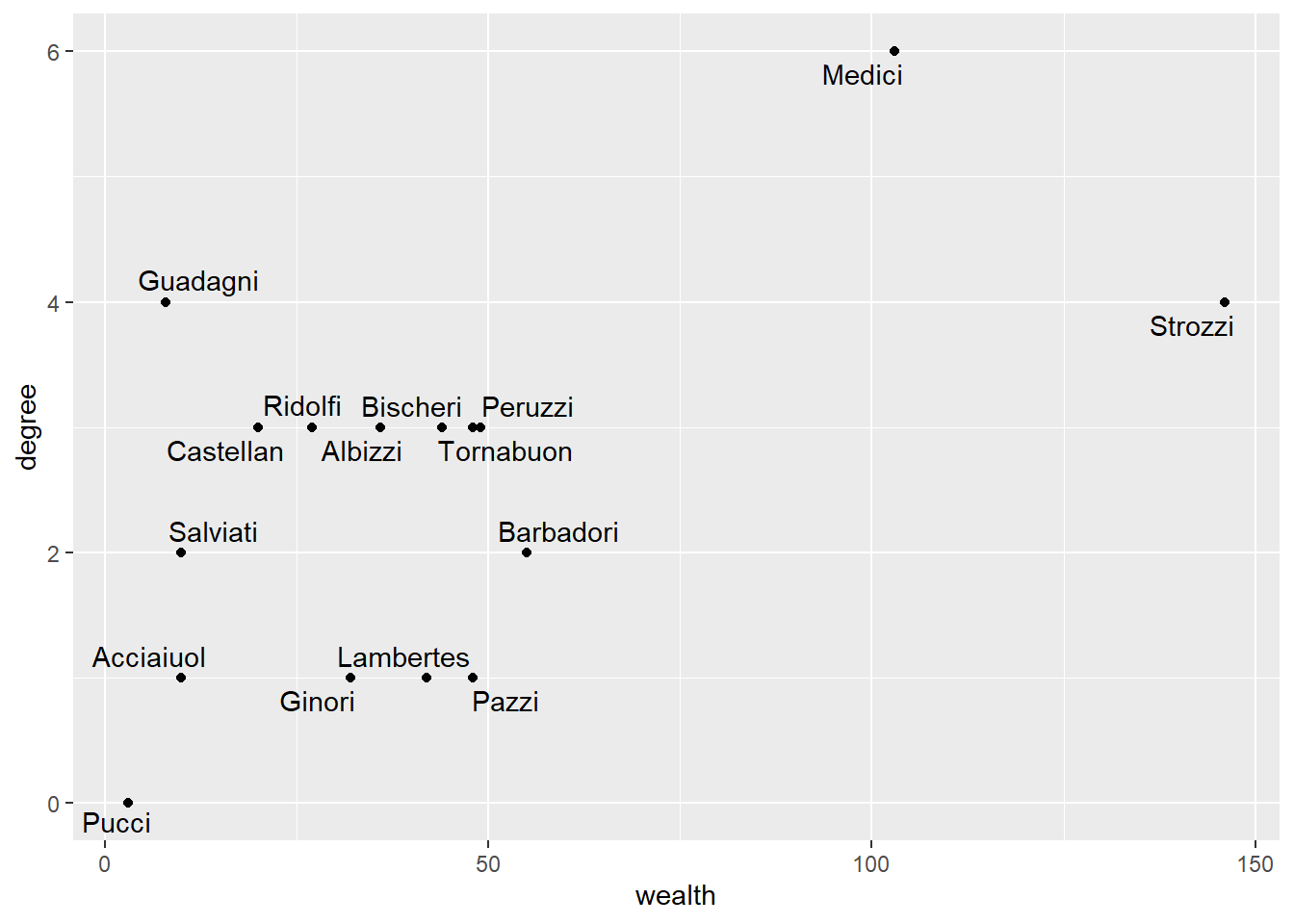

ggplotly(grafflor3)

## Warning in geom2trace.default(dots[[1L]][[1L]], dots[[2L]][[1L]], dots[[3L]][[1L]]): geom_GeomTextRepel() has yet to be implemented in plotly.
##   If you'd like to see this geom implemented,
##   Please open an issue with your example code at
##   https://github.com/ropensci/plotly/issues

Grau versus riqueza de diferentes famílias em Florença. Observe a alta riqueza e grau da família Medici.

Vemos que a família Medici tinha alto grau e riqueza. A família Medici tinha menos riqueza do que os Strozzi, mas tinha um grau superior.

---

A rede terrorista de Bali

Agora traçamos outra rede, a rede terrorista de Bali. Koschade (2006) realizou uma análise de rede social do Jemaah Islamiyah (uma organização militante armada) célula que foi responsável pelos atentados de Bali em 2002, em que 202 pessoas foram mortas.

Células terroristas trabalham em segredo e quem fala com quem é uma característica fundamental de como eles trabalham. Essa análise ajuda a entender seu funcionamento. Os dados de Bali são um objeto de rede, disponível no pacote UserNetR (Luke 2018).

Você pode baixar o arquivo de dados aqui

#library(UserNetR)
#data("Bali")
#class(Bali)
## [1] "network"

Convertemos a rede em um tbl_graph:

#Bali_t <- as_tbl_graph(Bali)
#Bali_t

Existem 17 nós e 63 arestas. Nós plotamos a rede com a função ggnetplot que criamos.

#ggnetplot(Bali)

Samudra (o comandante de campo) estava no centro da rede, com a maior interação com os outros.

Agora traçamos a rede com nós classificados pelo papel do membro; isso nos dá uma visão geral maior em comparação à figura anterior. O Team Lima foi o grupo de apoio da operação.

#Bali_g <- ggnetwork(Bali) 

#ggplot(Bali_g, aes(x,y, xend = xend, yend = yend)) +
             #     geom_edges(col = "tomato",
            #      alpha = 0.6) +
            #      geom_nodetext_repel(aes(label = role), size = 3) +
           #       theme_blank()

---

Simulando a formação de uma rede

Como as redes se formam? Dois modelos diferentes de formação de rede, que resultam em muito diferentes tipos de redes, são:

1: Modelo de Erdos Renyi de redes aleatórias onde dois nós se conectam ou não com uma determinada probabilidade, aleatoriamente, e;

2: Modelo de Barabasi e Albert onde as redes se formam ao longo do tempo e a cada novo nó prefere se conectar a nós bem conectados.

Agora traçamos algumas simulações de redes. Primeiro consideramos um Erdos Renyi simulação, onde o número de nós é ne a probabilidade de uma borda conectar quaisquer dois vértices são p. De acordo com Barabasi e Bonabeau (2003, p. 62), “Em 1959, com o objetivo de descrever as redes vistas nas comunicações e nas ciências da vida, Erdos e Renyi sugeriu que tais sistemas poderiam ser efetivamente modelados conectando seus nós com links colocados aleatoriamente.”

rg <- play_erdos_renyi(n = 30, p = 0.2, directed = FALSE)

class(rg)

## [1] "tbl_graph" "igraph"

rg2 <- rg %>%
activate(nodes) %>%
mutate(Deg = centrality_degree())

rg3 <- rg2 %>%
activate(nodes) %>%
as_tibble

Plotamos a distribuição de grau emergente da simulação Erdos Renyi. A distribuição é em forma de sino.

grafrg3<-ggplot(rg3, aes(x = Deg)) +
geom_bar()

ggplotly(grafrg3)

O código abaixo plota a rede:

rg_g <- asNetwork(rg2)
rg_g <- ggnetwork(rg_g, layout ="kamadakawai")

grafrg_g<-ggplot(rg_g, aes(x,y, xend = xend, yend = yend)) +
geom_edges(col = "tomato") +
geom_nodes(aes(size = Deg),
alpha = 0.4, #size = 1, 
col= "black") +
theme_blank()

ggplotly(grafrg_g)

Barabasi e Albert (1999) propuseram um modelo baseado no conceito de anexo preferencial. Um novo nó que se junta a uma rede vai preferir ligar-se a nós que são mais conectados. Eles escreveram (1999, p. 509), “Sistemas tão diversos quanto redes genéticas ou a World Wide Web são melhor descritos como redes com topologia complexa. Uma propriedade comum de muitas redes grandes é que as conectividades do vértice seguem uma distribuição de lei de potência sem escala. Este recurso foi considerado uma consequência de dois mecanismos genéricos: (i) as redes se expandem continuamente pela adição de novos vértices, e (ii) novos vértices se anexam preferencialmente a sites que já estão bem conectado.”

Agora traçamos gráficos relacionados à simulação de tal modelo de formação de rede.

ba <- play_barabasi_albert(n = 30, power = 1, directed = FALSE)

class(ba)

## [1] "tbl_graph" "igraph"

ba2 <- ba %>%
activate(nodes) %>%
mutate(Deg = centrality_degree())

ba3 <- ba2 %>%
activate(nodes) %>%
as_tibble

ggrg3 <- ggplot(rg3, aes(x = Deg)) + 
  geom_bar()
ggba3 <- ggplot(ba3, aes(x = Deg)) +
  geom_bar()

library(gridExtra)

grid.arrange(ggrg3, ggba3, ncol = 2)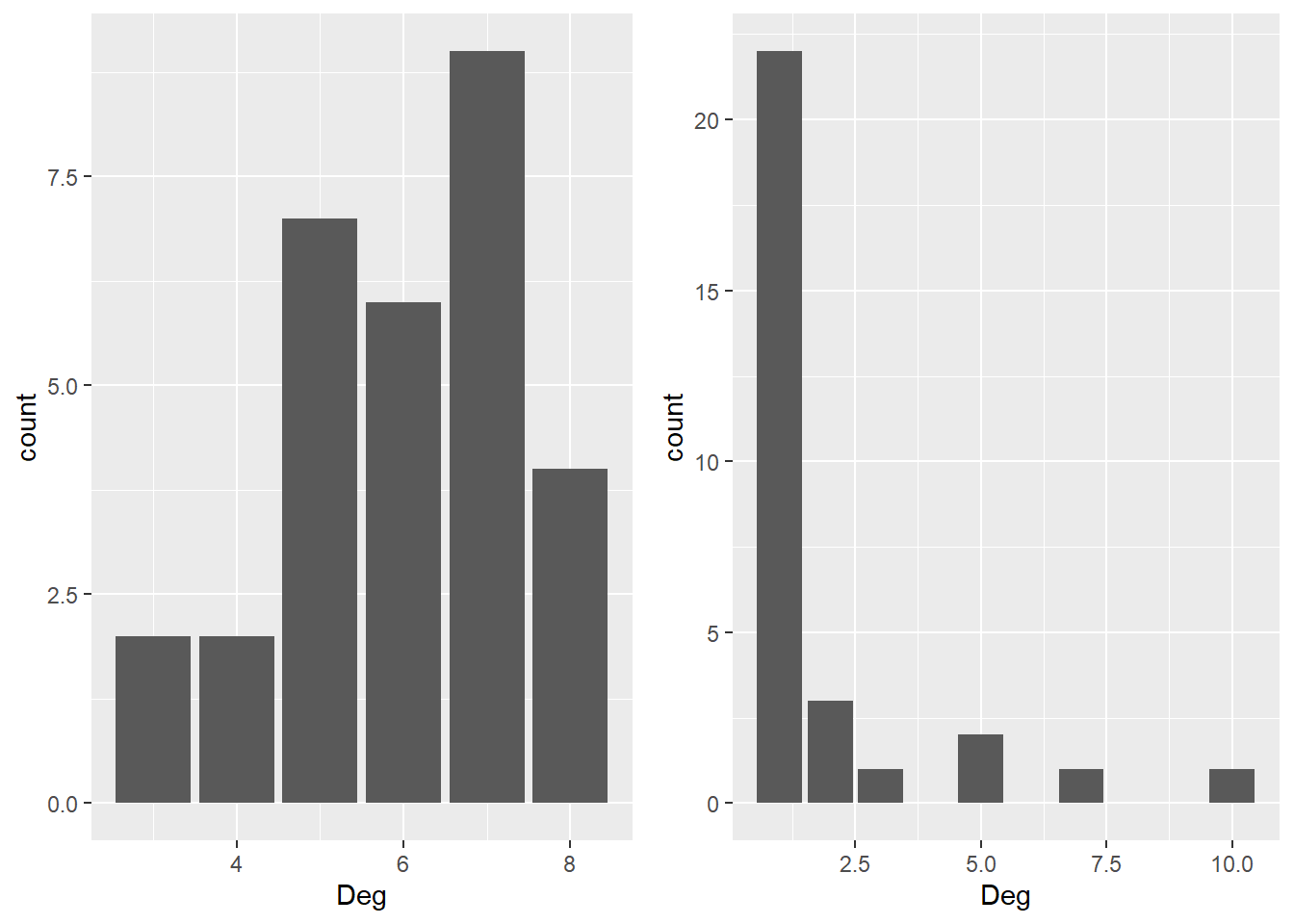

A Figura a seguir contrasta a distribuição de grau das redes originadas dos modelos de Erdos Renyi e Barabasi Albert.

ba_g <- asNetwork(ba2)
ba_g <- ggnetwork(ba_g, layout ="kamadakawai")

Distribuição de graus para Erdos Renyi (esquerda) e Barabasi Albert (direita). No primeiro, nós são conectados por arestas aleatoriamente e com uma determinada probabilidade; no último, conforme a rede cresce, um novo nó tem mais probabilidade de se anexar a um nó que está bem conectado

ggrg <- ggplot(rg_g, aes(x,y, xend = xend, yend = yend)) +
geom_edges(col = "tomato") +
geom_nodes(aes(size = Deg),
alpha = 0.4, #size = 1,
col = "black") +
theme_blank()

ggplotly(ggrg)

ggba <- ggplot(ba_g, aes(x,y, xend = xend, yend = yend)) +
geom_edges(col = "tomato") +
geom_nodes(aes(size = Deg),
alpha = 0.4 , #size = betw,
col = "black") +
theme_blank()
#geom_nodetext(aes(label = vertex.names),
#col = "black", size = 5) +

ggplotly(ggba)

grid.arrange(ggrg, ggba, ncol = 2)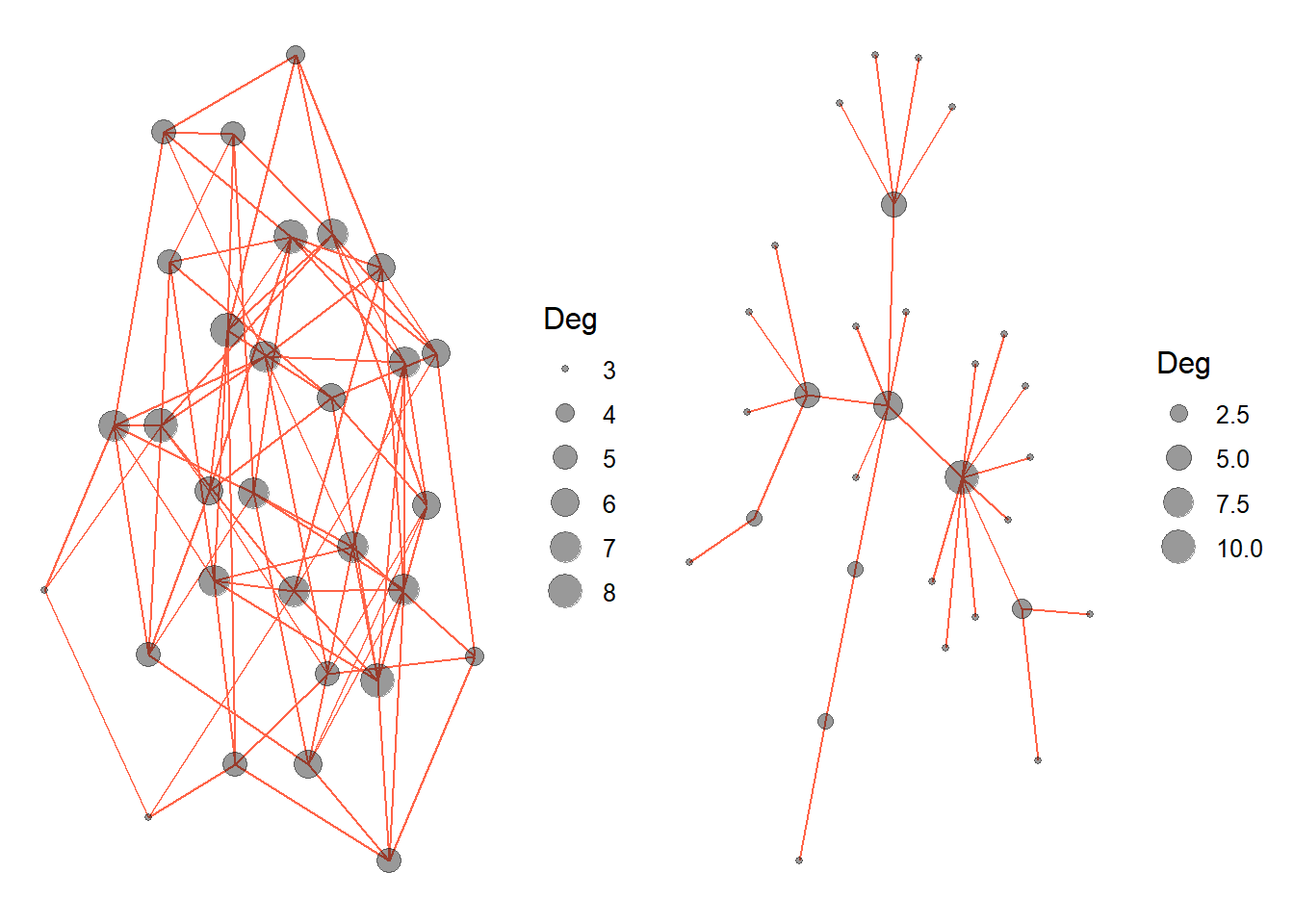

Diagrama de rede para Erdos Renyi (à esquerda) e Barabasi Albert (à direita). No primeiro, nós são conectados por arestas aleatoriamente e com uma determinada probabilidade; no último, conforme a rede cresce, um novo nó tem mais probabilidade de se anexar a um nó que está bem conectado.

O modelo Barabasi e Albert nos dá uma distribuição de graus muito diferente e gráfico de rede. O modelo de distribuição de grau de Barabasi e Albert é positivamente enviesado.

---

Exercício proposto

Tente executar a simulação para o modelo de Barabasi e Albert com n = 500. O que você observa?

---

A rede de produção de bens elétricos automotivos

Amighini e Gorgoni (2014) estudaram a reorganização internacional da produção automotiva.

A produção de automóveis usa fontes de componentes muito dispersas geograficamente. Dados relacionados a um dos componentes da produção automotiva em 2016, elétrico e as peças elétricas, ELEnet16, estão disponíveis no pacote ITNR (Smith 2018).

library(tidygraph)
library(ITNr)
data("ELEnet16")
class(ELEnet16)

## [1] "igraph"

usamos então tidygraph

ELE <- as_tbl_graph(ELEnet16)
class(ELE)

## [1] "tbl_graph" "igraph"

summary(ELE)

## IGRAPH a9d0bc0 DNW- 99 725 -- 
## + attr: name (v/c), id (v/c), regionNAME (v/c), region (v/n), income (v/n), GDP (v/n), GDPPC (v/n), logGDP (v/n), logGDPPC (v/n), GDPgrowth
## | (v/c), FDI (v/c), VAL (e/c), Share (e/n), weight (e/n)

Vamos traçar a rede, mas primeiro temos que fazer alguma troca de dados.

library(ggnetwork)

ELE_n <- asNetwork(ELE)
ELE_g <- ggnetwork(ELE_n)

str(ELE_g$regionNAME)

##  chr [1:824] "Middle East & North Africa (all income levels)" "Europe & Central Asia (all income levels)" "Europe & Central Asia (all income levels)" ...

ELE_g <- ELE_g %>%
mutate(nome_regiao = factor(regionNAME))

library(tidyverse)

ELE_g <- ELE_g %>%
mutate(nome_regiao = fct_recode(nome_regiao,
"Sub-SahAfr" =
"Sub-Saharan Africa (all income levels)",
"mEast&NAf" =
"Middle East & North Africa (all income levels)",
"LatAm&Car" =
"Latin America & Caribbean (all income levels)",
"Eur&CAsia" =
"Europe & Central Asia (all income levels)",
"EAsia&Pac" =
"East Asia & Pacific (all income levels)" ))

g<-ggplot(ELE_g, aes(x,y, xend = xend, yend = yend, col = nome_regiao)) +
geom_edges(color = "grey70") +
geom_nodes(alpha = 0.6, size = 5) +
theme_blank() +
theme(legend.position = "right") +
scale_colour_brewer(palette = "Dark2")



ggplotly(g)

O diagrama da rede de produção automática apóia a observação por Amighini e Gorgoni (2014, p. 923) que a produção de automóveis é “uma das mais atividades geograficamente fragmentadas no setor manufatureiro, com produção processos divididos em diferentes fases realizados em diferentes países.” Argumentando por a relevância de uma abordagem de rede, eles escrevem, “Abordagens tradicionais (como modelos gravitacionais) consideram apenas a relação entre os países i e j, assumindo que isso é independente de qualquer outra relação i e j estabelecer com outros países.”

Agora calculamos uma medida de graus externos ponderada. Os pesos das bordas são a proporção do comércio global.

ELE2 <- ELE %>%
activate(nodes) %>%
mutate(outdeg = centrality_degree(weights =
weight, mode = "out")) %>%
as_tibble()

Listamos os 10 principais países em medida de graus externos ponderados

ELE3 <- ELE2 %>%
select("name","regionNAME","outdeg") %>%
arrange(-outdeg)

library(knitr)
library(kableExtra)

kbl(cbind(ELE3)) %>%
  kable_paper() %>%
  scroll_box(width = "800px", height = "200px")

name	regionNAME	outdeg
CHN	East Asia & Pacific (all income levels)	22.9228108
KOR	East Asia & Pacific (all income levels)	10.6658851
JPN	East Asia & Pacific (all income levels)	8.7375358
USA	North America	8.4507279
MEX	Latin America & Caribbean (all income levels)	6.1197466
DEU	Europe & Central Asia (all income levels)	5.4831568
THA	East Asia & Pacific (all income levels)	2.7367629
CZE	Europe & Central Asia (all income levels)	2.3451855
MYS	East Asia & Pacific (all income levels)	2.2949618
VNM	East Asia & Pacific (all income levels)	2.2115654
ESP	Europe & Central Asia (all income levels)	1.9095539
POL	Europe & Central Asia (all income levels)	1.7769126
FRA	Europe & Central Asia (all income levels)	1.5679878
PRT	Europe & Central Asia (all income levels)	1.2762522
ITA	Europe & Central Asia (all income levels)	1.2743380
IDN	East Asia & Pacific (all income levels)	1.1485071
SGP	East Asia & Pacific (all income levels)	0.9281924
AUT	Europe & Central Asia (all income levels)	0.7726277
GBR	Europe & Central Asia (all income levels)	0.7155103
NLD	Europe & Central Asia (all income levels)	0.6624759
BEL	Europe & Central Asia (all income levels)	0.5300051
PHL	East Asia & Pacific (all income levels)	0.5116046
HUN	Europe & Central Asia (all income levels)	0.5024800
HKG	East Asia & Pacific (all income levels)	0.4400544
SVK	Europe & Central Asia (all income levels)	0.4358441
SVN	Europe & Central Asia (all income levels)	0.4285757
SWE	Europe & Central Asia (all income levels)	0.4182780
ARE	Middle East & North Africa (all income levels)	0.3818188
CHE	Europe & Central Asia (all income levels)	0.3030341
BRA	Latin America & Caribbean (all income levels)	0.2783451
IND	South Asia	0.2175908
SAU	Middle East & North Africa (all income levels)	0.1923101
GRC	Europe & Central Asia (all income levels)	0.1725001
COL	Latin America & Caribbean (all income levels)	0.1679914
BGR	Europe & Central Asia (all income levels)	0.1573381
CAN	North America	0.1236998
TUR	Europe & Central Asia (all income levels)	0.1070227
RUS	Europe & Central Asia (all income levels)	0.0860195
DNK	Europe & Central Asia (all income levels)	0.0789268
TGO	Sub-Saharan Africa (all income levels)	0.0788443
MKD	Europe & Central Asia (all income levels)	0.0650305
FIN	Europe & Central Asia (all income levels)	0.0607348
KAZ	Europe & Central Asia (all income levels)	0.0588727
NOR	Europe & Central Asia (all income levels)	0.0584381
DOM	Latin America & Caribbean (all income levels)	0.0576310
ISR	Middle East & North Africa (all income levels)	0.0481167
LTU	Europe & Central Asia (all income levels)	0.0357120
AUS	East Asia & Pacific (all income levels)	0.0350658
NZL	East Asia & Pacific (all income levels)	0.0336288
BLR	Europe & Central Asia (all income levels)	0.0325069
ARG	Latin America & Caribbean (all income levels)	0.0306616
IRL	Europe & Central Asia (all income levels)	0.0299613
QAT	Middle East & North Africa (all income levels)	0.0292315
LVA	Europe & Central Asia (all income levels)	0.0276366
ZAF	Sub-Saharan Africa (all income levels)	0.0232367
OMN	Middle East & North Africa (all income levels)	0.0225194
BRN	East Asia & Pacific (all income levels)	0.0222548
ECU	Latin America & Caribbean (all income levels)	0.0221554
KEN	Sub-Saharan Africa (all income levels)	0.0177513
KWT	Middle East & North Africa (all income levels)	0.0165538
UKR	Europe & Central Asia (all income levels)	0.0161487
GHA	Sub-Saharan Africa (all income levels)	0.0143611
MAR	Middle East & North Africa (all income levels)	0.0135324
TUN	Middle East & North Africa (all income levels)	0.0131153
BIH	Europe & Central Asia (all income levels)	0.0114570
GTM	Latin America & Caribbean (all income levels)	0.0112455
LUX	Europe & Central Asia (all income levels)	0.0106074
NGA	Sub-Saharan Africa (all income levels)	0.0106073
LBY	Middle East & North Africa (all income levels)	0.0101250
PAN	Latin America & Caribbean (all income levels)	0.0000000
AZE	Europe & Central Asia (all income levels)	0.0000000
BFA	Sub-Saharan Africa (all income levels)	0.0000000
BOL	Latin America & Caribbean (all income levels)	0.0000000
BWA	Sub-Saharan Africa (all income levels)	0.0000000
CHL	Latin America & Caribbean (all income levels)	0.0000000
CRI	Latin America & Caribbean (all income levels)	0.0000000
CYP	Europe & Central Asia (all income levels)	0.0000000
DZA	Middle East & North Africa (all income levels)	0.0000000
EGY	Middle East & North Africa (all income levels)	0.0000000
EST	Europe & Central Asia (all income levels)	0.0000000
ETH	Sub-Saharan Africa (all income levels)	0.0000000
HND	Latin America & Caribbean (all income levels)	0.0000000
HRV	Europe & Central Asia (all income levels)	0.0000000
JAM	Latin America & Caribbean (all income levels)	0.0000000
JOR	Middle East & North Africa (all income levels)	0.0000000
KHM	East Asia & Pacific (all income levels)	0.0000000
LBN	Middle East & North Africa (all income levels)	0.0000000
LKA	South Asia	0.0000000
MLI	Sub-Saharan Africa (all income levels)	0.0000000
MMR	East Asia & Pacific (all income levels)	0.0000000
NAM	Sub-Saharan Africa (all income levels)	0.0000000
PAK	South Asia	0.0000000
PER	Latin America & Caribbean (all income levels)	0.0000000
PRY	Latin America & Caribbean (all income levels)	0.0000000
SLV	Latin America & Caribbean (all income levels)	0.0000000
TZA	Sub-Saharan Africa (all income levels)	0.0000000
UGA	Sub-Saharan Africa (all income levels)	0.0000000
URY	Latin America & Caribbean (all income levels)	0.0000000
PSE	Middle East & North Africa (all income levels)	0.0000000

Os dados de 2016 mostram que China, Coreia e Japão foram os três primeiros países na medida outdegree valorizada. Amighini e Gorgoni (2014) estimaram que o os três principais países em 1998 foram Alemanha, EUA e França; em 2008 os três primeiros países foram China, Alemanha e Japão. Verificamos nossos cálculos com o em funções no ITNr.

ITN3 <- ITNcentrality(ELEnet16) %>%
as_tibble() %>%
arrange(-Weighted.Out.Degree)

kbl(cbind(ITN3)) %>%
  kable_paper() %>%
  scroll_box(width = "800px", height = "200px")

NAMES	Weighted.Out.Degree	Binary.Out.Degree	Weighted.In.Degree	Binary.In.Degree	Weighted.Degree.All	Binary.Degree.All	Betweenness	Closeness	Eigenvector	Hub	Authority
CHN	22.9228	76	7.1466	17	22.9228	93	0.1115	0.3368	0.8780	1.0000	0.6708
KOR	10.6659	48	2.5313	21	10.6659	69	0.1337	0.3286	0.4977	0.8490	0.5558
JPN	8.7375	32	3.3107	13	8.7375	45	0.0262	0.2847	0.5156	0.7079	0.6096
USA	8.4507	45	18.1518	28	8.4507	73	0.0487	0.2847	1.0000	0.7963	0.9152
MEX	6.1197	14	3.8618	12	6.1197	26	0.0122	0.2835	0.6433	0.2555	0.5334
DEU	5.4832	46	7.8152	32	5.4832	78	0.0382	0.2887	0.2935	0.8275	1.0000
THA	2.7368	31	0.6748	10	2.7368	41	0.0310	0.3368	0.1401	0.5660	0.4880
CZE	2.3452	19	1.2332	17	2.3452	36	0.0252	0.2759	0.0630	0.4148	0.6273
MYS	2.2950	14	0.8295	9	2.2950	23	0.0061	0.2712	0.1268	0.3154	0.4635
VNM	2.2116	29	0.0000	0	2.2116	29	0.0000	0.2666	0.0717	0.6473	0.0000
ESP	1.9096	20	1.9754	22	1.9096	42	0.0456	0.3029	0.0754	0.4547	0.8543
POL	1.7769	26	1.3433	18	1.7769	44	0.0550	0.2917	0.0521	0.5219	0.7640
FRA	1.5680	29	3.6285	26	1.5680	55	0.0285	0.2880	0.1087	0.5954	0.9167
PRT	1.2763	12	0.2397	5	1.2763	17	0.0056	0.2622	0.0270	0.3219	0.2207
ITA	1.2743	28	2.2394	22	1.2743	50	0.0454	0.3054	0.0522	0.5616	0.8277
IDN	1.1485	23	0.5850	8	1.1485	31	0.0148	0.2620	0.0610	0.5028	0.4117
SGP	0.9282	12	0.7868	13	0.9282	25	0.0076	0.2478	0.0681	0.2559	0.6348
AUT	0.7726	15	1.0101	15	0.7726	30	0.0378	0.2963	0.0438	0.3825	0.6682
GBR	0.7155	19	3.3002	26	0.7155	45	0.0331	0.2886	0.1116	0.4376	0.9139
NLD	0.6625	12	2.3972	24	0.6625	36	0.0528	0.2892	0.1076	0.2770	0.8096
BEL	0.5300	10	1.5254	18	0.5300	28	0.0369	0.2778	0.0419	0.2472	0.7970
PHL	0.5116	9	0.3844	6	0.5116	15	0.0059	0.2792	0.0205	0.2004	0.2990
HUN	0.5025	9	0.6329	12	0.5025	21	0.0063	0.2680	0.0262	0.2352	0.5614
HKG	0.4401	11	5.0964	12	0.4401	23	0.0022	0.2495	0.2725	0.2448	0.5447
SVK	0.4358	5	0.5373	8	0.4358	13	0.0062	0.2535	0.0215	0.1433	0.4277
SVN	0.4286	11	0.1737	6	0.4286	17	0.0122	0.2942	0.0052	0.2795	0.2665
SWE	0.4183	15	1.4989	18	0.4183	33	0.0182	0.2615	0.0458	0.3247	0.6862
ARE	0.3818	6	0.8260	16	0.3818	22	0.0286	0.2910	0.0374	0.1371	0.7174
CHE	0.3030	8	0.4810	10	0.3030	18	0.0054	0.2740	0.0260	0.2162	0.5427
BRA	0.2783	5	1.1272	13	0.2783	18	0.0175	0.2431	0.0542	0.0666	0.6107
IND	0.2176	8	1.9489	12	0.2176	20	0.0216	0.2500	0.0936	0.1598	0.5630
SAU	0.1923	7	0.7232	12	0.1923	19	0.0215	0.2509	0.0298	0.0848	0.5305
GRC	0.1725	5	0.1199	5	0.1725	10	0.0086	0.2588	0.0057	0.1289	0.2520
COL	0.1680	6	0.1781	3	0.1680	9	0.0124	0.2377	0.0171	0.0705	0.2149
BGR	0.1573	7	0.0529	4	0.1573	11	0.0424	0.3269	0.0030	0.2079	0.2511
CAN	0.1237	2	3.4415	12	0.1237	14	0.0007	0.2406	0.2156	0.0616	0.5724
TUR	0.1070	5	0.9999	14	0.1070	19	0.0060	0.2779	0.0325	0.0999	0.6739
RUS	0.0860	2	1.3175	25	0.0860	27	0.0021	0.2823	0.0393	0.0069	0.8658
DNK	0.0789	3	0.2876	8	0.0789	11	0.0205	0.2532	0.0067	0.0875	0.3438
TGO	0.0788	1	0.0000	0	0.0788	1	0.0000	0.0935	0.0029	0.0187	0.0000
MKD	0.0650	1	0.0000	0	0.0650	1	0.0000	0.1030	0.0000	0.0090	0.0000
FIN	0.0607	3	0.2102	6	0.0607	9	0.0042	0.2619	0.0066	0.0532	0.3276
KAZ	0.0589	1	0.0620	2	0.0589	3	0.0000	0.2055	0.0016	0.0291	0.0818
NOR	0.0584	3	0.2445	8	0.0584	11	0.0025	0.2707	0.0102	0.0810	0.4362
DOM	0.0576	1	0.2287	4	0.0576	5	0.0090	0.2210	0.0175	0.0187	0.1678
ISR	0.0481	3	0.1913	8	0.0481	11	0.0230	0.2704	0.0079	0.0495	0.3456
LTU	0.0357	2	0.0484	3	0.0357	5	0.0096	0.2441	0.0006	0.0467	0.1102
AUS	0.0351	2	1.4324	15	0.0351	17	0.0140	0.2797	0.0628	0.0370	0.6774
NZL	0.0336	1	0.1116	4	0.0336	5	0.0000	0.2566	0.0078	0.0187	0.2609
BLR	0.0325	1	0.1036	3	0.0325	4	0.0000	0.1944	0.0019	0.0291	0.1242
ARG	0.0307	1	0.4888	6	0.0307	7	0.0000	0.2391	0.0191	0.0205	0.3129
IRL	0.0300	1	0.0793	2	0.0300	3	0.0000	0.1768	0.0027	0.0307	0.1168
QAT	0.0292	1	0.0983	5	0.0292	6	0.0065	0.2526	0.0040	0.0027	0.2482
LVA	0.0276	2	0.0217	1	0.0276	3	0.0000	0.2126	0.0001	0.0066	0.0424
ZAF	0.0232	2	0.2859	8	0.0232	10	0.0130	0.2680	0.0141	0.0000	0.4751
OMN	0.0225	1	0.0786	3	0.0225	4	0.0025	0.2418	0.0007	0.0178	0.0870
BRN	0.0223	1	0.0000	0	0.0223	1	0.0000	0.1922	0.0008	0.0187	0.0000
ECU	0.0222	2	0.0343	2	0.0222	4	0.0043	0.2160	0.0013	0.0131	0.0870
KEN	0.0178	1	0.0000	0	0.0178	1	0.0000	0.1042	0.0000	0.0027	0.0000
KWT	0.0166	1	0.1114	5	0.0166	6	0.0044	0.2420	0.0041	0.0189	0.2348
UKR	0.0161	1	0.0000	0	0.0161	1	0.0000	0.1957	0.0000	0.0291	0.0000
GHA	0.0144	1	0.0225	1	0.0144	2	0.0000	0.2424	0.0020	0.0187	0.0812
MAR	0.0135	1	0.0744	4	0.0135	5	0.0093	0.2606	0.0023	0.0287	0.2305
TUN	0.0131	1	0.0000	0	0.0131	1	0.0000	0.2199	0.0001	0.0278	0.0000
BIH	0.0115	1	0.0000	0	0.0115	1	0.0000	0.2112	0.0001	0.0211	0.0000
GTM	0.0112	1	0.0923	4	0.0112	5	0.0045	0.2908	0.0055	0.0187	0.2357
LUX	0.0106	1	0.0000	0	0.0106	1	0.0000	0.2226	0.0002	0.0336	0.0000
NGA	0.0106	1	0.0904	4	0.0106	5	0.0054	0.2687	0.0047	0.0187	0.2185
LBY	0.0101	1	0.0000	0	0.0101	1	0.0000	0.2484	0.0004	0.0187	0.0000
PAN	0.0000	0	0.0955	3	0.0000	3	0.0000	0.2039	0.0030	0.0000	0.1681
AZE	0.0000	0	0.0168	1	0.0000	1	0.0000	0.2173	0.0011	0.0000	0.0812
BFA	0.0000	0	0.0441	2	0.0000	2	0.0000	0.2235	0.0024	0.0000	0.1485
BOL	0.0000	0	0.0232	1	0.0000	1	0.0000	0.1915	0.0015	0.0000	0.0812
BWA	0.0000	0	0.0122	1	0.0000	1	0.0000	0.2035	0.0000	0.0000	0.0000
CHL	0.0000	0	0.2367	5	0.0000	5	0.0000	0.1911	0.0110	0.0000	0.2217
CRI	0.0000	0	0.0789	3	0.0000	3	0.0000	0.2108	0.0048	0.0000	0.1667
CYP	0.0000	0	0.0116	1	0.0000	1	0.0000	0.2400	0.0004	0.0000	0.0690
DZA	0.0000	0	0.1453	6	0.0000	6	0.0000	0.2505	0.0034	0.0000	0.3378
EGY	0.0000	0	0.1480	7	0.0000	7	0.0000	0.2579	0.0034	0.0000	0.3150
EST	0.0000	0	0.0494	3	0.0000	3	0.0000	0.2504	0.0007	0.0000	0.0861
ETH	0.0000	0	0.1041	3	0.0000	3	0.0000	0.2501	0.0047	0.0000	0.1681
HND	0.0000	0	0.0613	3	0.0000	3	0.0000	0.2623	0.0035	0.0000	0.1667
HRV	0.0000	0	0.0488	4	0.0000	4	0.0000	0.2652	0.0002	0.0000	0.1444
JAM	0.0000	0	0.0113	1	0.0000	1	0.0000	0.1886	0.0000	0.0000	0.0057
JOR	0.0000	0	0.0190	1	0.0000	1	0.0000	0.1716	0.0000	0.0000	0.0069
KHM	0.0000	0	0.0106	1	0.0000	1	0.0000	0.2500	0.0007	0.0000	0.0812
LBN	0.0000	0	0.0734	3	0.0000	3	0.0000	0.2216	0.0028	0.0000	0.1962
LKA	0.0000	0	0.0685	3	0.0000	3	0.0000	0.2449	0.0027	0.0000	0.1402
MLI	0.0000	0	0.0378	2	0.0000	2	0.0000	0.2303	0.0020	0.0000	0.1485
MMR	0.0000	0	0.0164	1	0.0000	1	0.0000	0.2194	0.0011	0.0000	0.0812
NAM	0.0000	0	0.0110	1	0.0000	1	0.0000	0.2082	0.0000	0.0000	0.0000
PAK	0.0000	0	0.1782	2	0.0000	2	0.0000	0.1472	0.0098	0.0000	0.0815
PER	0.0000	0	0.1594	6	0.0000	6	0.0000	0.2877	0.0067	0.0000	0.3338
PRY	0.0000	0	0.0927	3	0.0000	3	0.0000	0.2011	0.0031	0.0000	0.1326
SLV	0.0000	0	0.0384	2	0.0000	2	0.0000	0.2194	0.0021	0.0000	0.0854
TZA	0.0000	0	0.0694	2	0.0000	2	0.0000	0.1270	0.0034	0.0000	0.0815
UGA	0.0000	0	0.0190	1	0.0000	1	0.0000	0.2077	0.0012	0.0000	0.0812
URY	0.0000	0	0.0374	2	0.0000	2	0.0000	0.2464	0.0009	0.0000	0.0866
PSE	0.0000	0	0.0101	1	0.0000	1	0.0000	0.2137	0.0000	0.0000	0.0040

Plotamos a distribuição graus externos ponderada; é positivamente distorcida.

grafELE2<-ggplot(ELE2, aes(x = outdeg)) +
geom_histogram(bins = 30)

ggplotly(grafELE2)

Vamos agora representar graficamente a distribuição de grau externo ponderada (outdeg) por região.

ELE2 <- ELE2 %>%
mutate(region_name = factor(regionNAME))

library(tidyverse)

ELE2 <- ELE2 %>%
mutate(region_name = fct_recode(region_name,
"Sub-SahAf" =
"Sub-Saharan Africa (all income levels)",
"mEast&NAf" =
"Middle East & North Africa (all income levels)",
"LatAm&Car" =
"Latin America & Caribbean (all income levels)",
"Eur&CAsia" =
"Europe & Central Asia (all income levels)",
"EAsia&Pac" =
"East Asia & Pacific (all income levels)" ))


grafregiao<-ggplot(ELE2, aes(x = region_name, y = outdeg)) +
geom_boxplot() +
coord_flip()

ggplotly(grafregiao)

Distribuição grau externo ponderada por região da rede de produtos elétricos automotivos 2016

A distribuição de graus da região mostra a importância do Leste Asiático e da Pacífico, América do Norte e Europa e Ásia Central.

---

Para continuar aprendendo

O curso de Scott Page (sem data) sobre Model Thinking tem palestras curtas muito claras sobre redes.

• Barabasi (2016) tem um vídeo maravilhoso: As redes estão por toda parte.

 

• Jackson’s (2014) possui um artigo que vincula redes a comportamentos econômicos.

• Douglas Luke (2015) forneceu um guia detalhado e claro para usar R para análise de rede.

 

---

 

Referências

Barabasi, A. 2016. Networks are everywhere. https://www.youtube.com/watch?v=c867FlzxZ9Y.

Barabasi, A.-L., and R. Albert. 1999. Emergence of scaling in random networks. Science 286:509–512.

Barabasi, A.-L., and E. Bonabeau. 2003. Scale-Free networks. Scientific American 288: 60–69.

Bojanowski, M. 2015. intergraph: Coercion routines for network data objects. R Package Version 2.0-2. http://mbojan.github.io/intergraph

Briatte, F. 2016. ggnetwork: Geometries to plot networks with ’ggplot2’. R Package Version (5): 1. https://CRAN.R-project.org/package=ggnetwork.

Csardi, G., and T. Nepusz. 2006. The igraph software package for complex network research. InterJournal Complex Systems 1695: 2006. http://igraph.org.

Jackson, M.O. 2008. Social and Economic Networks. Princeton: Princeton University Press.

Jackson, M.O. 2014. Networks in the understanding of economic behaviors. Journal of Economic Perspectives 28 (4): 3–22.

Padgett, J.F., and C.K. Ansell. 1993. AJS 98 (6): 1259–1319.

Pedersen, T.L. 2019. tidygraph: A tidy API for graph manipulation. R Package Version 1 (1): 2. https://CRAN.R-project.org/package=tidygraph.

Schoch, D. 2017. netrankr: An R package to analyze partial rankings in networks.

Koschade, S. 2006. A social network analysis of jemaah islamiyah: the applications to counterterrorism and intelligence. Studies in Conflict and Terrorism 29: 559–575.

Luke, D. 2015. A user’s guide to network analysis in R. Berlin: Springer.

Luke, D. 2018. UserNetR: data sets for a user’s guide to network analysis in R. R Package Version 2: 26.

Smith, M. 2018. ITNr: Analysis of the international trade network. R Package Version (3): https://CRAN.R-project.org/package=ITNr.

Wickham, H. 2017. tidyverse: easily install and load the ’Tidyverse’. R Package Version 1 (2): 1. https://CRAN.R-project.org/package=tidyverse.