Forecasting de séries temporais com algoritmos de machine learning
Rodrigo Hermont Ozon
junho 22, 2021
Economic Time Series Forecasting
Este post explora um teste com o pacote modeltime para forecasting de séries temporais combinando algoritmos de machine learning.
Anunciai-nos as coisas que ainda hão de vir, para que saibamos que sois deuses; ou fazei bem, ou fazei mal, para que nos assombremos, e juntamente o vejamos. Isaías 41:23

\[\\[1in]\]
Carrego as bibliotecas necessárias
library(xgboost)
library(earth)
library(tidymodels)
library(modeltime)
library(modeltime.ensemble)
library(tidyverse)
library(lubridate)
library(timetk)
library(quantmod)
library(tsibble)
library(tsibbledata)
library(dplyr)
library(tidyverse)
library(data.table)
library(tidyr)
library(TSstudio)
library(h2o)
library(modeltime.h2o)Baixo os dados e separo amostra de treino
Utilizarei novamente os mesmos dados das cotações do milho CORN negociados na bolsa de Chicago:
CORN <- getSymbols("CORN", auto.assign = FALSE,
from = "1994-01-01", end = Sys.Date())
glimpse(CORN)An 'xts' object on 2010-06-09/2021-06-21 containing:
Data: num [1:2778, 1:6] 25.1 25.5 25.9 26 26.2 ...
- attr(*, "dimnames")=List of 2
..$ : NULL
..$ : chr [1:6] "CORN.Open" "CORN.High" "CORN.Low" "CORN.Close" ...
Indexed by objects of class: [Date] TZ: UTC
xts Attributes:
List of 2
$ src : chr "yahoo"
$ updated: POSIXct[1:1], format: "2021-06-22 07:36:24"periodicity(CORN)Daily periodicity from 2010-06-09 to 2021-06-21 CORN <- CORN %>%
as.data.table() %>%
as_tibble()
class(CORN)[1] "tbl_df" "tbl" "data.frame"glimpse(CORN)Rows: 2,778
Columns: 7
$ index <date> 2010-06-09, 2010-06-10, 2010-06-11, 2010-06-14, 2010-06~
$ CORN.Open <dbl> 25.12, 25.46, 25.88, 25.99, 26.24, 26.26, 26.20, 26.22, ~
$ CORN.High <dbl> 25.25, 25.46, 25.88, 26.11, 26.24, 26.44, 26.20, 26.60, ~
$ CORN.Low <dbl> 25.12, 25.46, 25.79, 25.99, 25.97, 26.20, 25.82, 26.22, ~
$ CORN.Close <dbl> 25.15, 25.46, 25.79, 26.11, 25.97, 26.32, 26.08, 26.39, ~
$ CORN.Volume <dbl> 1700, 200, 500, 2200, 7000, 2400, 1600, 3100, 9500, 2870~
$ CORN.Adjusted <dbl> 25.15, 25.46, 25.79, 26.11, 25.97, 26.32, 26.08, 26.39, ~CORN %>%
plot_time_series(index, CORN.Close, .interactive = FALSE)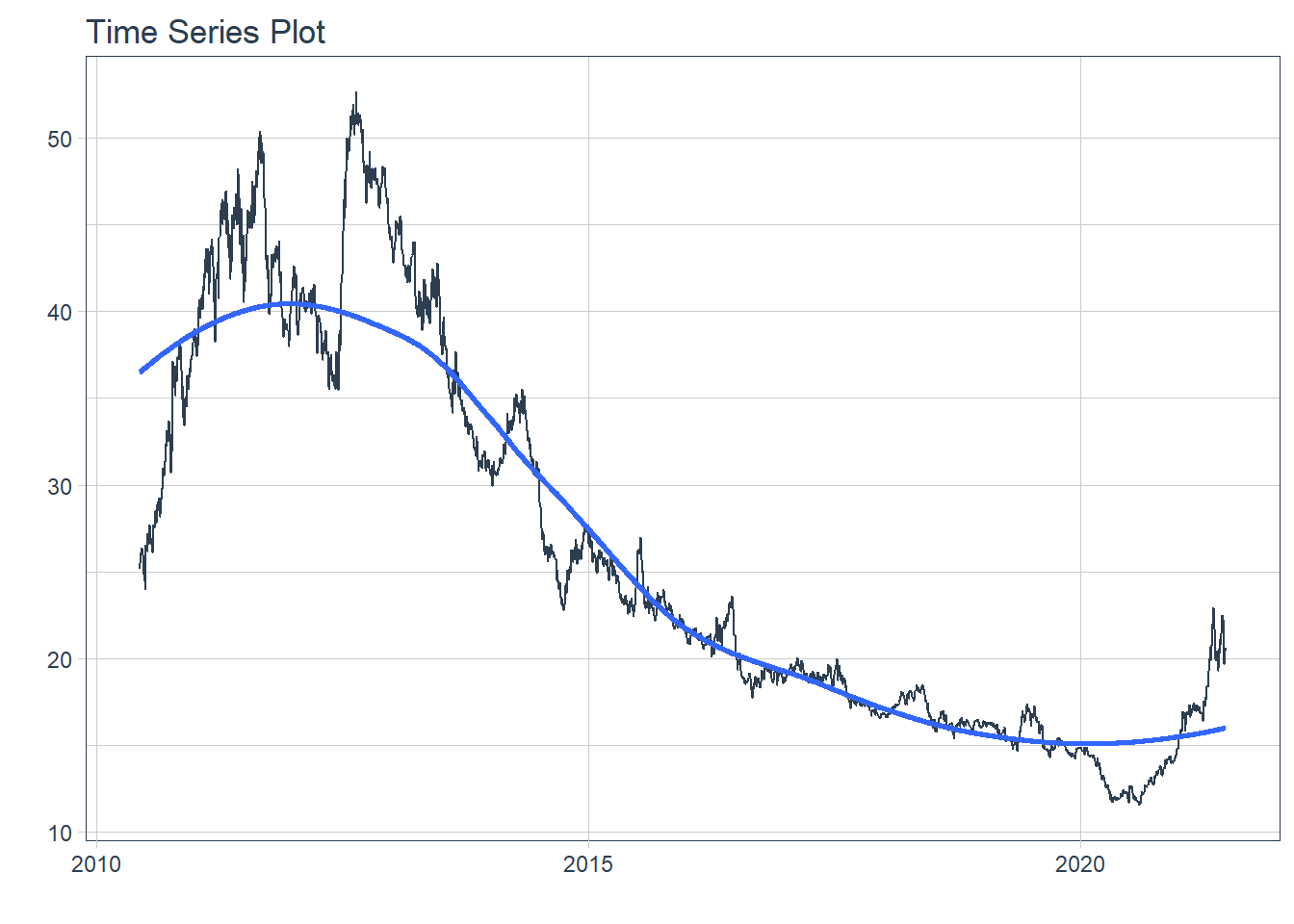
Separa a série temporal numa proporção 70/30
splits <- initial_time_split(CORN, prop = 0.8)Estimando os modelos univariados contra o tempo
Os modelos aqui testados são 14, sendo que eles contemplam:
Família ARIMA e com erros XGBoost;
Ajuste/Alisamento Exponencial e com ajustes sazonais e também modelo Croston e Theta
TBATS;
propheteprophet_xgboostNaive e SNaive
Rede Neural Artificial com componente Auto Regressivo
# Modelo 1: auto_arima ----
model_fit_arima_no_boost <- arima_reg() %>%
set_engine(engine = "auto_arima") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 2: arima_boost ----
model_fit_arima_boosted <- arima_boost(
min_n = 2,
learn_rate = 0.9
) %>%
set_engine(engine = "auto_arima_xgboost") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 3: ets ----
model_fit_ets <- exp_smoothing() %>%
set_engine(engine = "ets") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 4: tbats ----
model_fit_tbats <- seasonal_reg() %>%
set_engine(engine = "tbats") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 5: prophet xgb ----
model_fit_prophet_xb <- prophet_boost(
learn_rate = 0.8 ) %>%
set_engine("prophet_xgboost") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 6: stlm_ets ----
model_fit_stlm_ets <- seasonal_reg() %>%
set_engine("stlm_ets") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 7: stlm arima ----
model_fit_stlm_arima <- seasonal_reg() %>%
set_engine("stlm_arima") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 8: arima xgb padrao ----
model_fit_arima_padrao <-arima_boost(
# Padroes p, d, q
seasonal_period = 7,
non_seasonal_ar = 5,
non_seasonal_differences = 1,
non_seasonal_ma = 3,
seasonal_ar = 1,
seasonal_differences = 0,
seasonal_ma = 1,
# XGBoost
tree_depth = 6,
learn_rate = 0.8
) %>%
set_engine("arima_xgboost") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 9: ets padrao ----
model_fit_ets_padrao <- exp_smoothing(
seasonal_period = 7, # padrao de 7 dias de trade
error = "multiplicative",
trend = "additive",
season = "multiplicative"
) %>%
set_engine("ets") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 10: ets croston ----
model_fit_ets_croston <- exp_smoothing(
smooth_level = 0.2
) %>%
set_engine("croston") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 11: ets theta ----
model_fit_ets_theta <- exp_smoothing(
) %>%
set_engine("theta") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 12: naive ----
model_fit_naive <- naive_reg(
) %>%
set_engine("naive") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 13: snaive ----
model_fit_snaive <- naive_reg(
seasonal_period = 7
) %>%
set_engine("snaive") %>%
fit(CORN.Close ~ index,
data = training(splits))# Modelo 14: rede neural autoregressiva ----
model_fit_nnetar <- nnetar_reg(
) %>%
set_engine("nnetar")
set.seed(123)
model_fit_nnetar <- model_fit_nnetar %>%
fit(CORN.Close ~ index,
data = training(splits))Comparativo de perfomance preditiva
Avalio o ajuste de cada método para a mesma amostra da série temporal:
models_tbl <- modeltime_table(
# -- Modelo -- -- Numero --
model_fit_arima_no_boost, # Modelo 1
model_fit_arima_boosted, # Modelo 2
model_fit_ets, # Modelo 3
model_fit_tbats, # Modelo 4
model_fit_prophet_xb, # Modelo 5
model_fit_stlm_ets, # Modelo 6
model_fit_stlm_arima, # Modelo 7
model_fit_arima_padrao, # Modelo 8
model_fit_ets_padrao, # Modelo 9
model_fit_ets_croston, # Modelo 10
model_fit_ets_theta, # Modelo 11
model_fit_naive, # Modelo 12
model_fit_snaive, # Modelo 13
model_fit_nnetar # Modelo 14
)
models_tbl# Modeltime Table
# A tibble: 14 x 3
.model_id .model .model_desc
<int> <list> <chr>
1 1 <fit[+]> ARIMA(2,1,0)
2 2 <fit[+]> ARIMA(0,1,2)
3 3 <fit[+]> ETS(M,A,N)
4 4 <fit[+]> BATS(0, {0,0}, -, -)
5 5 <fit[+]> PROPHET
6 6 <fit[+]> SEASONAL DECOMP: ETS(M,A,N)
7 7 <fit[+]> SEASONAL DECOMP: ARIMA(0,1,0)
8 8 <fit[+]> ARIMA(5,1,3)(1,0,1)[7]
9 9 <fit[+]> ETS(M,AD,M)
10 10 <fit[+]> CROSTON METHOD
11 11 <fit[+]> THETA METHOD
12 12 <fit[+]> NAIVE
13 13 <fit[+]> SNAIVE [7]
14 14 <fit[+]> NNAR(1,1,10)[5] Compara a acurácia
models_tbl %>%
modeltime_calibrate(new_data = testing(splits)) %>%
modeltime_accuracy(
metric_set = metric_set(
mape,
smape,
mae,
rmse,
rsq # R^2
)
)# A tibble: 14 x 8
.model_id .model_desc .type mape smape mae rmse rsq
<int> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 ARIMA(2,1,0) Test 13.0 12.5 1.91 2.41 2.44e-5
2 2 ARIMA(0,1,2) Test 13.0 12.5 1.91 2.41 3.86e-5
3 3 ETS(M,A,N) Test 13.3 15.5 2.26 3.61 7.95e-2
4 4 BATS(0, {0,0}, -, -) Test 12.9 12.5 1.91 2.41 NA
5 5 PROPHET Test 12.5 13.5 2.02 2.97 3.84e-2
6 6 SEASONAL DECOMP: ETS(M,A,~ Test 13.1 15.2 2.22 3.56 7.95e-2
7 7 SEASONAL DECOMP: ARIMA(0,~ Test 13.0 12.6 1.91 2.42 3.13e-5
8 8 ARIMA(5,1,3)(1,0,1)[7] Test 13.0 12.5 1.91 2.41 3.94e-6
9 9 ETS(M,AD,M) Test 12.6 12.3 1.87 2.40 2.49e-3
10 10 CROSTON METHOD Test 13.4 12.8 1.96 2.44 NA
11 11 THETA METHOD Test 12.3 14.1 2.08 3.34 7.95e-2
12 12 NAIVE Test 12.9 12.5 1.90 2.41 NA
13 13 SNAIVE [7] Test 13.2 12.7 1.93 2.43 1.98e-6
14 14 NNAR(1,1,10)[5] Test 16.3 14.9 2.29 2.77 3.50e-3Veremos o modelo prophet p. ex.:
list(model_fit_prophet_xb) %>%
as_modeltime_table()# Modeltime Table
# A tibble: 1 x 3
.model_id .model .model_desc
<int> <list> <chr>
1 1 <fit[+]> PROPHET Calibração dos modelos
calibration_tbl <- models_tbl %>%
modeltime_calibrate(new_data = testing(splits), quiet = FALSE)
calibration_tbl# Modeltime Table
# A tibble: 14 x 5
.model_id .model .model_desc .type .calibration_data
<int> <list> <chr> <chr> <list>
1 1 <fit[+]> ARIMA(2,1,0) Test <tibble [556 x 4]>
2 2 <fit[+]> ARIMA(0,1,2) Test <tibble [556 x 4]>
3 3 <fit[+]> ETS(M,A,N) Test <tibble [556 x 4]>
4 4 <fit[+]> BATS(0, {0,0}, -, -) Test <tibble [556 x 4]>
5 5 <fit[+]> PROPHET Test <tibble [556 x 4]>
6 6 <fit[+]> SEASONAL DECOMP: ETS(M,A,N) Test <tibble [556 x 4]>
7 7 <fit[+]> SEASONAL DECOMP: ARIMA(0,1,0) Test <tibble [556 x 4]>
8 8 <fit[+]> ARIMA(5,1,3)(1,0,1)[7] Test <tibble [556 x 4]>
9 9 <fit[+]> ETS(M,AD,M) Test <tibble [556 x 4]>
10 10 <fit[+]> CROSTON METHOD Test <tibble [556 x 4]>
11 11 <fit[+]> THETA METHOD Test <tibble [556 x 4]>
12 12 <fit[+]> NAIVE Test <tibble [556 x 4]>
13 13 <fit[+]> SNAIVE [7] Test <tibble [556 x 4]>
14 14 <fit[+]> NNAR(1,1,10)[5] Test <tibble [556 x 4]>Projeção (forecasting)
calibration_tbl %>%
modeltime_forecast(
new_data = testing(splits),
actual_data = CORN
) %>%
plot_modeltime_forecast(
.legend_max_width = 25, # For mobile screens
.interactive = TRUE
)Modelo combinado de projeção
O modelo do tipo ensemble é um modelo misto com os pesos ajustados pela acurácia de cada um dos 14 univariados estimados até aqui
# Modelo 15: ensemble ----
model_fit_ensemble <- models_tbl %>%
ensemble_weighted(
loadings = c
(
#-- Peso -- # -- Modelo --
1, # Modelo 1
2, # Modelo 2
5, # Modelo 3
6, # Modelo 4
10, # Modelo 5
9, # Modelo 6
8, # Modelo 7
1, # Modelo 8
7, # Modelo 9
2, # Modelo 10
2, # Modelo 11
2, # Modelo 12
1, # Modelo 13
10 # Modelo 14
),
scale_loadings = TRUE
)
model_fit_ensemble-- Modeltime Ensemble -------------------------------------------
Ensemble of 14 Models (WEIGHTED)
# Modeltime Table
# A tibble: 14 x 4
.model_id .model .model_desc .loadings
<int> <list> <chr> <dbl>
1 1 <fit[+]> ARIMA(2,1,0) 0.0152
2 2 <fit[+]> ARIMA(0,1,2) 0.0303
3 3 <fit[+]> ETS(M,A,N) 0.0758
4 4 <fit[+]> BATS(0, {0,0}, -, -) 0.0909
5 5 <fit[+]> PROPHET 0.152
6 6 <fit[+]> SEASONAL DECOMP: ETS(M,A,N) 0.136
7 7 <fit[+]> SEASONAL DECOMP: ARIMA(0,1,0) 0.121
8 8 <fit[+]> ARIMA(5,1,3)(1,0,1)[7] 0.0152
9 9 <fit[+]> ETS(M,AD,M) 0.106
10 10 <fit[+]> CROSTON METHOD 0.0303
11 11 <fit[+]> THETA METHOD 0.0303
12 12 <fit[+]> NAIVE 0.0303
13 13 <fit[+]> SNAIVE [7] 0.0152
14 14 <fit[+]> NNAR(1,1,10)[5] 0.152 Construimos a projeção com o modelo misto:
# Calibragem
calibration_tbl <- modeltime_table(
model_fit_ensemble
) %>%
modeltime_calibrate(testing(splits), quiet = FALSE)
# Forecast vs amostra de teste (dados originais pra frente antes do corte pra amostra treino)
calibration_tbl %>%
modeltime_forecast(
new_data = testing(splits),
actual_data = CORN
) %>%
plot_modeltime_forecast(.interactive = TRUE)Reamostragens
A reamostragem de séries temporais é uma estratégia importante para avaliar a estabilidade dos modelos ao longo do tempo. No entanto, é um tanto quanto penoso fazer isso, pois requer vários loops for para gerar as previsões para vários modelos e, potencialmente, vários grupos de séries temporais.
resamples_tscv <- training(splits) %>%
time_series_cv(
assess = "2 years",
initial = "5 years",
skip = "1 years",
# Normally we do more than one slice, but this speeds up the example
slice_limit = 1
)
# Fit and generate resample predictions
model_fit_ensemble_resample <- calibration_tbl %>%
modeltime_fit_resamples(
resamples = resamples_tscv,
control = control_resamples(verbose = TRUE)
)-- Fitting Resamples --------------------------------------------
0.2 sec elapsed# A new data frame is created from the Modeltime Table
# with a column labeled, '.resample_results'
model_fit_ensemble_resample# Modeltime Table
# A tibble: 1 x 6
.model_id .model .model_desc .type .calibration_da~ .resample_resul~
<int> <list> <chr> <chr> <list> <list>
1 1 <ensembl~ ENSEMBLE (WEIGHTE~ Test <tibble [556 x ~ <lgl [1]> Plota o gráfico
model_fit_ensemble_resample %>%
plot_modeltime_resamples(.interactive = TRUE)Revisão das projeções (forecast forward)
Constrói a projeção para fora da amostra desde a última observação para os próximos 24 meses:
refit_tbl <- calibration_tbl %>%
modeltime_refit(data = CORN)
refit_tbl %>%
modeltime_forecast(h = "2 years", actual_data = CORN) %>%
plot_modeltime_forecast(
.legend_max_width = 25, # For mobile screens
.interactive = TRUE
)Estimativa dos modelos bivariados do tipo preço x volume (fluxo de oferta e demanda)
Na forma bivariada inserimos o volume de negociação como variável explicativa, ainda mesmo que esperando uma performance estatística inferior, sabemos que pelo princípio econômico, a volatilidade é facilmente capturada ao observarmos os picos de volume negociados diariamente.
# Modelo 1: auto_arima ----
model_fit_arima_no_boost_biv <- arima_reg() %>%
set_engine(engine = "auto_arima") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 2: arima_boost ----
model_fit_arima_boosted_biv <- arima_boost(
min_n = 2,
learn_rate = 0.9
) %>%
set_engine(engine = "auto_arima_xgboost") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 3: ets ----
model_fit_ets_biv <- exp_smoothing() %>%
set_engine(engine = "ets") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 4: tbats ----
model_fit_tbats_biv <- seasonal_reg() %>%
set_engine(engine = "tbats") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 5: prophet xgb ----
model_fit_prophet_xb_biv <- prophet_boost(
learn_rate = 0.8 ) %>%
set_engine("prophet_xgboost") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 6: stlm_ets ----
model_fit_stlm_ets_biv <- seasonal_reg() %>%
set_engine("stlm_ets") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 7: stlm arima ----
model_fit_stlm_arima_biv <- seasonal_reg() %>%
set_engine("stlm_arima") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 8: arima xgb padrao ----
model_fit_arima_padrao_biv <-arima_boost(
# Padroes p, d, q
seasonal_period = 7,
non_seasonal_ar = 5,
non_seasonal_differences = 1,
non_seasonal_ma = 3,
seasonal_ar = 1,
seasonal_differences = 0,
seasonal_ma = 1,
# XGBoost
tree_depth = 6,
learn_rate = 0.8
) %>%
set_engine("arima_xgboost") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 9: ets padrao ----
model_fit_ets_padrao_biv <- exp_smoothing(
seasonal_period = 7, # padrao de 7 dias de trade
error = "multiplicative",
trend = "additive",
season = "multiplicative"
) %>%
set_engine("ets") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 10: ets croston ----
model_fit_ets_croston_biv <- exp_smoothing(
smooth_level = 0.2
) %>%
set_engine("croston") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 11: ets theta ----
model_fit_ets_theta_biv <- exp_smoothing(
) %>%
set_engine("theta") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 12: naive ----
model_fit_naive_biv <- naive_reg(
) %>%
set_engine("naive") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 13: snaive ----
model_fit_snaive_biv <- naive_reg(
seasonal_period = 7
) %>%
set_engine("snaive") %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))# Modelo 14: rede neural autoregressiva ----
model_fit_nnetar_biv <- nnetar_reg(
) %>%
set_engine("nnetar")
set.seed(123)
model_fit_nnetar_biv <- model_fit_nnetar_biv %>%
fit(CORN.Close ~ CORN.Volume + index,
data = training(splits))Comparativo de perfomance preditiva (bivariado)
Avalio o ajuste de cada método para a mesma amostra da série temporal:
models_tbl_bivariada <- modeltime_table(
# -- Modelo -- -- Numero --
model_fit_arima_no_boost_biv, # Modelo 1
model_fit_arima_boosted_biv, # Modelo 2
model_fit_ets_biv, # Modelo 3
model_fit_tbats_biv, # Modelo 4
model_fit_prophet_xb_biv, # Modelo 5
model_fit_stlm_ets_biv, # Modelo 6
model_fit_stlm_arima_biv, # Modelo 7
model_fit_arima_padrao_biv, # Modelo 8
model_fit_ets_padrao_biv, # Modelo 9
model_fit_ets_croston_biv, # Modelo 10
model_fit_ets_theta_biv, # Modelo 11
model_fit_naive_biv, # Modelo 12
model_fit_snaive_biv, # Modelo 13
model_fit_nnetar_biv # Modelo 14
)
models_tbl_bivariada# Modeltime Table
# A tibble: 14 x 3
.model_id .model .model_desc
<int> <list> <chr>
1 1 <fit[+]> REGRESSION WITH ARIMA(2,1,0) ERRORS
2 2 <fit[+]> ARIMA(0,1,2) W/ XGBOOST ERRORS
3 3 <fit[+]> ETS(M,A,N)
4 4 <fit[+]> BATS(0, {0,0}, -, -)
5 5 <fit[+]> PROPHET W/ XGBOOST ERRORS
6 6 <fit[+]> SEASONAL DECOMP: ETS(M,A,N)
7 7 <fit[+]> SEASONAL DECOMP: REGRESSION WITH ARIMA(0,1,0) ERRORS
8 8 <fit[+]> ARIMA(5,1,3)(1,0,1)[7] W/ XGBOOST ERRORS
9 9 <fit[+]> ETS(M,AD,M)
10 10 <fit[+]> CROSTON METHOD
11 11 <fit[+]> THETA METHOD
12 12 <fit[+]> NAIVE
13 13 <fit[+]> SNAIVE [7]
14 14 <fit[+]> NNAR(1,1,10)[5] Compara a acurácia (bivariado)
Tabela de avaliação da acurácia dos modelos bivariados no tempo:
models_tbl_bivariada %>%
modeltime_calibrate(new_data = testing(splits)) %>%
modeltime_accuracy(
metric_set = metric_set(
mape,
smape,
mae,
rmse,
rsq # R^2
)
)# A tibble: 14 x 8
.model_id .model_desc .type mape smape mae rmse rsq
<int> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 REGRESSION WITH ARIMA(2,1,~ Test 11.2 12.1 1.84 2.86 8.27e-2
2 2 ARIMA(0,1,2) W/ XGBOOST ER~ Test 13.1 12.6 1.92 2.47 1.53e-3
3 3 ETS(M,A,N) Test 13.3 15.5 2.26 3.61 7.95e-2
4 4 BATS(0, {0,0}, -, -) Test 12.9 12.5 1.91 2.41 NA
5 5 PROPHET W/ XGBOOST ERRORS Test 12.8 13.5 2.03 2.88 4.30e-3
6 6 SEASONAL DECOMP: ETS(M,A,N) Test 13.1 15.2 2.22 3.56 7.95e-2
7 7 SEASONAL DECOMP: REGRESSIO~ Test 13.0 12.6 1.92 2.42 3.40e-2
8 8 ARIMA(5,1,3)(1,0,1)[7] W/ ~ Test 13.1 12.7 1.93 2.46 5.58e-5
9 9 ETS(M,AD,M) Test 12.6 12.3 1.87 2.40 2.49e-3
10 10 CROSTON METHOD Test 13.4 12.8 1.96 2.44 NA
11 11 THETA METHOD Test 12.3 14.1 2.08 3.34 7.95e-2
12 12 NAIVE Test 12.9 12.5 1.90 2.41 NA
13 13 SNAIVE [7] Test 13.2 12.7 1.93 2.43 1.98e-6
14 14 NNAR(1,1,10)[5] Test 82.5 47.8 12.1 16.5 5.66e-2Veremos o modelo prophet p. ex.:
list(model_fit_prophet_xb) %>%
as_modeltime_table()# Modeltime Table
# A tibble: 1 x 3
.model_id .model .model_desc
<int> <list> <chr>
1 1 <fit[+]> PROPHET Calibração dos modelos (bivariado)
calibration_tbl_bivariada <- models_tbl %>%
modeltime_calibrate(new_data = testing(splits), quiet = FALSE)
calibration_tbl_bivariada# Modeltime Table
# A tibble: 14 x 5
.model_id .model .model_desc .type .calibration_data
<int> <list> <chr> <chr> <list>
1 1 <fit[+]> ARIMA(2,1,0) Test <tibble [556 x 4]>
2 2 <fit[+]> ARIMA(0,1,2) Test <tibble [556 x 4]>
3 3 <fit[+]> ETS(M,A,N) Test <tibble [556 x 4]>
4 4 <fit[+]> BATS(0, {0,0}, -, -) Test <tibble [556 x 4]>
5 5 <fit[+]> PROPHET Test <tibble [556 x 4]>
6 6 <fit[+]> SEASONAL DECOMP: ETS(M,A,N) Test <tibble [556 x 4]>
7 7 <fit[+]> SEASONAL DECOMP: ARIMA(0,1,0) Test <tibble [556 x 4]>
8 8 <fit[+]> ARIMA(5,1,3)(1,0,1)[7] Test <tibble [556 x 4]>
9 9 <fit[+]> ETS(M,AD,M) Test <tibble [556 x 4]>
10 10 <fit[+]> CROSTON METHOD Test <tibble [556 x 4]>
11 11 <fit[+]> THETA METHOD Test <tibble [556 x 4]>
12 12 <fit[+]> NAIVE Test <tibble [556 x 4]>
13 13 <fit[+]> SNAIVE [7] Test <tibble [556 x 4]>
14 14 <fit[+]> NNAR(1,1,10)[5] Test <tibble [556 x 4]>Projeção (forecasting) (bivariado)
calibration_tbl_bivariada %>%
modeltime_forecast(
new_data = testing(splits),
actual_data = CORN
) %>%
plot_modeltime_forecast(
.legend_max_width = 25, # For mobile screens
.interactive = TRUE
)Modelo combinado de projeção (bivariado)
O modelo do tipo ensemble é um modelo misto com os pesos ajustados pela acurácia de cada um dos 14 univariados estimados até aqui
# Modelo 15: ensemble ----
model_fit_ensemble_bivariada <- models_tbl_bivariada %>%
ensemble_weighted(
loadings = c
(
#-- Peso -- # -- Modelo --
1, # Modelo 1
10, # Modelo 2
5, # Modelo 3
6, # Modelo 4
10, # Modelo 5
9, # Modelo 6
8, # Modelo 7
10, # Modelo 8
7, # Modelo 9
2, # Modelo 10
2, # Modelo 11
2, # Modelo 12
1, # Modelo 13
6 # Modelo 14
),
scale_loadings = TRUE
)
model_fit_ensemble_bivariada-- Modeltime Ensemble -------------------------------------------
Ensemble of 14 Models (WEIGHTED)
# Modeltime Table
# A tibble: 14 x 4
.model_id .model .model_desc .loadings
<int> <list> <chr> <dbl>
1 1 <fit[+]> REGRESSION WITH ARIMA(2,1,0) ERRORS 0.0127
2 2 <fit[+]> ARIMA(0,1,2) W/ XGBOOST ERRORS 0.127
3 3 <fit[+]> ETS(M,A,N) 0.0633
4 4 <fit[+]> BATS(0, {0,0}, -, -) 0.0759
5 5 <fit[+]> PROPHET W/ XGBOOST ERRORS 0.127
6 6 <fit[+]> SEASONAL DECOMP: ETS(M,A,N) 0.114
7 7 <fit[+]> SEASONAL DECOMP: REGRESSION WITH ARIMA(0,1,0) E~ 0.101
8 8 <fit[+]> ARIMA(5,1,3)(1,0,1)[7] W/ XGBOOST ERRORS 0.127
9 9 <fit[+]> ETS(M,AD,M) 0.0886
10 10 <fit[+]> CROSTON METHOD 0.0253
11 11 <fit[+]> THETA METHOD 0.0253
12 12 <fit[+]> NAIVE 0.0253
13 13 <fit[+]> SNAIVE [7] 0.0127
14 14 <fit[+]> NNAR(1,1,10)[5] 0.0759Construimos a projeção com o modelo misto:
# Calibragem
calibration_tbl_bivariada <- modeltime_table(
model_fit_ensemble_bivariada
) %>%
modeltime_calibrate(testing(splits), quiet = FALSE)
# Forecast vs amostra de teste (dados originais pra frente antes do corte pra amostra treino)
calibration_tbl_bivariada %>%
modeltime_forecast(
new_data = testing(splits),
actual_data = CORN
) %>%
plot_modeltime_forecast(.interactive = TRUE)Reamostragens (bivariado)
A reamostragem de séries temporais é uma estratégia importante para avaliar a estabilidade dos modelos ao longo do tempo. No entanto, é um tanto quanto penoso fazer isso, pois requer vários loops for para gerar as previsões para vários modelos e, potencialmente, vários grupos de séries temporais.
resamples_tscv <- training(splits) %>%
time_series_cv(
assess = "2 years",
initial = "5 years",
skip = "1 years",
slice_limit = 1
)
# Fit and generate resample predictions
model_fit_ensemble_resample_bivariada <- calibration_tbl_bivariada %>%
modeltime_fit_resamples(
resamples = resamples_tscv,
control = control_resamples(verbose = TRUE)
)-- Fitting Resamples --------------------------------------------
0.02 sec elapsed# A new data frame is created from the Modeltime Table
# with a column labeled, '.resample_results'
model_fit_ensemble_resample_bivariada# Modeltime Table
# A tibble: 1 x 6
.model_id .model .model_desc .type .calibration_da~ .resample_resul~
<int> <list> <chr> <chr> <list> <list>
1 1 <ensembl~ ENSEMBLE (WEIGHTE~ Test <tibble [556 x ~ <lgl [1]> Revisão das projeções (forecast forward) (bivariado)
Constrói a projeção para fora da amostra desde a última observação para os próximos 24 meses:
refit_tbl_bivariada <- calibration_tbl_bivariada %>%
modeltime_refit(data = CORN)
refit_tbl_bivariada %>%
modeltime_forecast(h = "2 years", actual_data = CORN) %>%
plot_modeltime_forecast(
.legend_max_width = 25, # For mobile screens
.interactive = TRUE
)Modelo bivariado combinado
Seleciono somente alguns modelos que julguei como melhor ajuste:
models_tbl_selecao <- modeltime_table(
# -- Modelo -- -- Numero --
model_fit_arima_no_boost_biv, # Modelo 1
model_fit_arima_boosted_biv, # Modelo 2
model_fit_prophet_xb_biv, # Modelo 5
model_fit_arima_padrao_biv, # Modelo 8
)
models_tbl_selecaoFazemos a calibração
calibration_tbl_selecao <- models_tbl_selecao %>%
modeltime_calibrate(new_data = testing(splits), quiet = FALSE)
calibration_tbl_selecaoCriamos o ensemble:
model_fit_ensemble_selecao <- models_tbl_selecao %>%
ensemble_average(type = "mean")Construimos a projeção com o modelo misto:
# Calibragem
calibration_tbl_selecao <- modeltime_table(
model_fit_ensemble_selecao
) %>%
modeltime_calibrate(testing(splits), quiet = FALSE)
# Forecast vs amostra de teste (dados originais pra frente antes do corte pra amostra treino)
calibration_tbl_selecao %>%
modeltime_forecast(
new_data = testing(splits),
actual_data = CORN
) %>%
plot_modeltime_forecast(.interactive = TRUE)AutoML com o pacote h2o
O pacote h2o possui uma implementação automática de recomendação de modelo preditivo para os dados que o separamos.
H2o é uma biblioteca de código aberto, distribuída e baseada em Java para aplicações de machine learning. Ele tem APIs para R (o pacote h2o) e Python, e inclui aplicativos para modelos de aprendizagem supervisionados e não supervisionados. Isso inclui algoritmos como deep learning (DL), Gradient Boost Machine(GBM), XGBoost, Random Forest Distribuída (RF) e o Modelo Linear Generalizado (GLM).
A principal vantagem do pacote h2o é que ele se baseia em processamento distribuído e, portanto, pode ser usado na memória ou ampliado com o uso de computação externa potência. Além disso, os algoritmos do pacote h2o fornecem vários métodos para que possamos treinar e ajustar modelos de aprendizado de máquina, como o método de validação cruzada e a função grid search integrada.
O pacote h2o é baseado no uso de computação distribuída e paralela para acelerar o tempo de computação e possibilita escalonar para big data. Tudo isso é feito em qualquer parte da memória (com base na RAM interna do computador) ou processamento paralelo distribuído (para exemplo, AWS, Google Cloud e assim por diante) clusters. Portanto, vamos carregar o pacote e em seguida, definir o cluster na memória com a função h2o.init:
h2o.init(max_mem_size = "16G") Connection successful!
R is connected to the H2O cluster:
H2O cluster uptime: 2 minutes 12 seconds
H2O cluster timezone: America/Sao_Paulo
H2O data parsing timezone: UTC
H2O cluster version: 3.32.0.1
H2O cluster version age: 8 months and 13 days !!!
H2O cluster name: H2O_started_from_R_rodri_mfl031
H2O cluster total nodes: 1
H2O cluster total memory: 14.20 GB
H2O cluster total cores: 8
H2O cluster allowed cores: 8
H2O cluster healthy: TRUE
H2O Connection ip: localhost
H2O Connection port: 54321
H2O Connection proxy: NA
H2O Internal Security: FALSE
H2O API Extensions: Amazon S3, Algos, AutoML, Core V3, TargetEncoder, Core V4
R Version: R version 4.0.3 (2020-10-10) O comando h2o.init permite que você defina o tamanho da memória do cluster com o argumento max_mem_size. A saída da função, conforme mostrado no código anterior, fornece informações sobre a configuração do cluster.
Quaisquer dados usados em todo o processo de treinamento e teste dos modelos pelo pacote H2o deve ser carregado no próprio cluster. A função as.h2o nos permite transformar qualquer objeto data.frame em um cluster h2o:
CORN <- getSymbols("CORN", auto.assign = FALSE,
from = "1994-01-01", end = Sys.Date())
# Convete para tsibble
CORN <- CORN %>%
as.data.table() %>%
as_tsibble()
# Separa treino
treino <- CORN %>%
filter_index(~"2020-06") # Amostra de treino ate junho 2020
# Retiro os gaps implícitos
CORN <- CORN %>%
fill_gaps() %>%
fill(c(CORN.Open, CORN.High, CORN.Low, CORN.Close, CORN.Volume, CORN.Adjusted), .direction = "down")
print(CORN)# A tsibble: 4,031 x 7 [1D]
index CORN.Open CORN.High CORN.Low CORN.Close CORN.Volume CORN.Adjusted
<date> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 2010-06-09 25.1 25.2 25.1 25.2 1700 25.2
2 2010-06-10 25.5 25.5 25.5 25.5 200 25.5
3 2010-06-11 25.9 25.9 25.8 25.8 500 25.8
4 2010-06-12 25.9 25.9 25.8 25.8 500 25.8
5 2010-06-13 25.9 25.9 25.8 25.8 500 25.8
6 2010-06-14 26.0 26.1 26.0 26.1 2200 26.1
7 2010-06-15 26.2 26.2 26.0 26.0 7000 26.0
8 2010-06-16 26.3 26.4 26.2 26.3 2400 26.3
9 2010-06-17 26.2 26.2 25.8 26.1 1600 26.1
10 2010-06-18 26.2 26.6 26.2 26.4 3100 26.4
# ... with 4,021 more rows# Separo treino sem gaps implicitos
treino <- treino %>%
fill_gaps() %>%
fill(c(CORN.Open, CORN.High, CORN.Low, CORN.Close, CORN.Volume, CORN.Adjusted), .direction = "down")
print(treino)# A tsibble: 3,675 x 7 [1D]
index CORN.Open CORN.High CORN.Low CORN.Close CORN.Volume CORN.Adjusted
<date> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 2010-06-09 25.1 25.2 25.1 25.2 1700 25.2
2 2010-06-10 25.5 25.5 25.5 25.5 200 25.5
3 2010-06-11 25.9 25.9 25.8 25.8 500 25.8
4 2010-06-12 25.9 25.9 25.8 25.8 500 25.8
5 2010-06-13 25.9 25.9 25.8 25.8 500 25.8
6 2010-06-14 26.0 26.1 26.0 26.1 2200 26.1
7 2010-06-15 26.2 26.2 26.0 26.0 7000 26.0
8 2010-06-16 26.3 26.4 26.2 26.3 2400 26.3
9 2010-06-17 26.2 26.2 25.8 26.1 1600 26.1
10 2010-06-18 26.2 26.6 26.2 26.4 3100 26.4
# ... with 3,665 more rowstreino <- as.h2o(treino)
|
| | 0%
|
|======================================================================| 100%teste <- CORN %>%
filter_index("2020-06" ~ .)
teste <- as.h2o(teste)
|
| | 0%
|
|======================================================================| 100%Em seguida rodaremos o autoML para duas configurações:
univariada \(\rightarrow\) CORN.Close no tempo;
bivariada \(\rightarrow\) CORN.Close \(x\) CORN.Volume no tempo;
A função h2o.automl fornece uma abordagem de sistema automatizada para treinar, ajustar e testar vários algoritmos de ML antes de selecionar o modelo com melhor desempenho com base nas métricas de avaliação. Ele utiliza algoritmos como RF, GBM, DL e outros usando diferentes abordagens de ajuste.
autoML_univariada <- h2o.automl(training_frame = treino,
y = "CORN.Close",
nfolds = 5,
max_runtime_secs = 60*20,
seed = 1234)
|
| | 0%
07:44:25.640: AutoML: XGBoost is not available; skipping it.
|
|=== | 5%
|
|====== | 8%
|
|======= | 10%
|
|======== | 12%
|
|========== | 15%
|
|============ | 17%
|
|============== | 20%
|
|=============== | 22%
|
|================= | 24%
|
|================== | 26%
|
|==================== | 28%
|
|==================== | 29%
|
|========================= | 35%
|
|========================== | 37%
|
|=========================== | 38%
|
|=========================== | 39%
|
|============================ | 40%
|
|============================= | 41%
|
|============================= | 42%
|
|============================== | 42%
|
|============================== | 43%
|
|=============================== | 44%
|
|=============================== | 45%
|
|================================ | 45%
|
|================================ | 46%
|
|================================= | 47%
|
|================================= | 48%
|
|================================== | 48%
|
|================================== | 49%
|
|=================================== | 50%
|
|==================================== | 51%
|
|==================================== | 52%
|
|===================================== | 52%
|
|===================================== | 53%
|
|====================================== | 54%
|
|====================================== | 55%
|
|======================================= | 55%
|
|======================================= | 56%
|
|======================================== | 57%
|
|========================================= | 58%
|
|========================================= | 59%
|
|========================================== | 60%
|
|=========================================== | 61%
|
|=========================================== | 62%
|
|============================================ | 62%
|
|============================================ | 63%
|
|=============================================== | 68%
|
|================================================ | 68%
|
|================================================= | 70%
|
|================================================== | 71%
|
|===================================================== | 76%
|
|====================================================== | 77%
|
|======================================================= | 78%
|
|======================================================= | 79%
|
|========================================================= | 81%
|
|=========================================================== | 84%
|
|=========================================================== | 85%
|
|============================================================ | 85%
|
|============================================================= | 88%
|
|================================================================ | 92%
|
|=================================================================== | 96%
|
|======================================================================| 100%autoML_univariada@leaderboard model_id mean_residual_deviance
1 GBM_grid__1_AutoML_20210622_074425_model_9 0.0009374919
2 StackedEnsemble_BestOfFamily_AutoML_20210622_074425 0.0011375269
3 StackedEnsemble_AllModels_AutoML_20210622_074425 0.0011513922
4 GBM_grid__1_AutoML_20210622_074425_model_38 0.0016900971
5 GBM_grid__1_AutoML_20210622_074425_model_26 0.0018321366
6 GBM_grid__1_AutoML_20210622_074425_model_15 0.0019220423
rmse mse mae rmsle
1 0.03061849 0.0009374919 0.008650376 0.0009494086
2 0.03372724 0.0011375269 0.017379793 0.0011101063
3 0.03393217 0.0011513922 0.018748787 0.0011257065
4 0.04111079 0.0016900971 0.017911010 0.0013395347
5 0.04280347 0.0018321366 0.017527076 0.0013777139
6 0.04384110 0.0019220423 0.020225699 0.0014186983
[62 rows x 6 columns] autoML_bivariada <- h2o.automl(training_frame = treino,
y = "CORN.Close",
x = "CORN.Volume",
nfolds = 5,
max_runtime_secs = 60*20,
seed = 1234)
|
| | 0%
08:02:25.868: AutoML: XGBoost is not available; skipping it.
|
|==== | 6%
|
|===== | 8%
|
|====== | 8%
|
|======== | 12%
|
|=========== | 16%
|
|============== | 20%
|
|================= | 24%
|
|==================== | 28%
|
|====================== | 32%
|
|========================== | 37%
|
|========================== | 38%
|
|=========================== | 38%
|
|=========================== | 39%
|
|============================ | 40%
|
|============================================ | 63%
|
|============================================= | 65%
|
|============================================== | 65%
|
|============================================== | 66%
|
|=============================================== | 67%
|
|=============================================== | 68%
|
|================================================ | 68%
|
|================================================ | 69%
|
|================================================= | 70%
|
|================================================== | 71%
|
|===================================================== | 75%
|
|===================================================== | 76%
|
|====================================================== | 78%
|
|======================================================= | 78%
|
|======================================================= | 79%
|
|======================================================== | 80%
|
|=========================================================== | 84%
|
|=========================================================== | 85%
|
|============================================================ | 86%
|
|============================================================= | 87%
|
|============================================================= | 88%
|
|================================================================ | 92%
|
|======================================================================| 100%autoML_bivariada@leaderboard model_id mean_residual_deviance
1 StackedEnsemble_BestOfFamily_AutoML_20210622_080225 99.63547
2 StackedEnsemble_AllModels_AutoML_20210622_080225 99.98401
3 GBM_grid__1_AutoML_20210622_080225_model_32 104.88266
4 GBM_grid__1_AutoML_20210622_080225_model_34 105.00627
5 GBM_grid__1_AutoML_20210622_080225_model_26 105.13606
6 GBM_grid__1_AutoML_20210622_080225_model_29 105.67575
rmse mse mae rmsle
1 9.981757 99.63547 8.264394 0.3579126
2 9.999200 99.98401 8.289894 0.3586062
3 10.241223 104.88266 8.530085 0.3671610
4 10.247257 105.00627 8.687456 0.3671139
5 10.253587 105.13606 8.532638 0.3672908
6 10.279871 105.67575 8.739143 0.3684461
[63 rows x 6 columns] Você pode ver que, neste caso, os modelos de topo são modelos os modelos sugeridos com diferentes configurações de tunelamento. Selecionaremos o modelo líder e testaremos seu desempenho no conjunto de teste:
# ------- Dados da estimativa do tipo CORN.Close x tempo ---------------------------------------------------------
teste$pred_autoML_univariada <- h2o.predict(autoML_univariada@leader, teste)
|
| | 0%
|
|======================================================================| 100%teste_univariada <- as.data.frame(teste)
mape_autoML_univariada <- mean(abs(teste_univariada$CORN.Close - teste_univariada$pred_autoML_univariada) / teste_univariada$CORN.Close)
mape_autoML_univariada[1] 0.001543803# ------- Dados da estimativa do tipo CORN.Close x CORN.Volume + tempo -------------------------------------------
teste$pred_autoML_bivariada <- h2o.predict(autoML_bivariada@leader, teste)
|
| | 0%
|
|======================================================================| 100%teste_bivariada <- as.data.frame(teste)
mape_autoML_bivariada <- mean(abs(teste_bivariada$CORN.Close - teste_bivariada$pred_autoML_bivariada) / teste_bivariada$CORN.Close)
mape_autoML_bivariada[1] 0.989757Vamos comparar no gráfico como ficaria a performance dentro e fora da amostra do autoML do pacote h2o:
[continuar escrevendo…]
Referências
Business Science in R bloggers Introducing Modeltime Recursive: Tidy Autoregressive Forecasting with Lags, Disponível em: https://www.r-bloggers.com/2021/04/introducing-modeltime-recursive-tidy-autoregressive-forecasting-with-lags/
Business Science in R bloggers Introducing Modeltime: Tidy Time Series Forecasting using Tidymodels, Disponível em: https://www.r-bloggers.com/2020/06/introducing-modeltime-tidy-time-series-forecasting-using-tidymodels/
Business Science, Github, Ensemble Algorithms for Time Series Forecasting with Modeltime, Disponível em: https://business-science.github.io/modeltime.ensemble/ acesso em junho de 2021.
CRAN, Getting Started with Modeltime, Disponível em: https://cran.r-project.org/web/packages/modeltime/vignettes/getting-started-with-modeltime.html
CRAN, Package ‘modeltime’, Disponível em: https://cran.r-project.org/web/packages/modeltime/modeltime.pdf junho de 2021.
CRAN, Package ‘modeltime.ensemble’ Disponível em: https://cran.r-project.org/web/packages/modeltime.ensemble/modeltime.ensemble.pdf junho de 2021.
CRAN, Package ‘modeltime.resample’ Disponível em: https://cran.r-project.org/web/packages/modeltime.resample/modeltime.resample.pdf junho de 2021.
Github, Ensemble Algorithms for Time Series Forecasting with Modeltime, Disponível em: https://github.com/business-science/modeltime.ensemble acesso em junho de 2021.
HANSEN, B. Econometrics, University of Wisconsin, Department of Economics. Disponível em: https://www.ssc.wisc.edu/~bhansen/econometrics/Econometrics.pdf March 11, 2021.
USAI, D. Time Series Machine Learning Analysis and Demand Forecasting with H2O & TSstudio, Disponível em: https://rpubs.com/DiegoUsai/565288