Seleção de Portfólio com Otimização Multicritério
Rodrigo Hermont Ozon
Last Update: agosto 25, 2024
start_time <- Sys.time()Seleção de Portfólio (Phd Student)

Documento tutorial de exemplo de testagem de metodologia multicritério para seleção de portfólio.
Pacotes
library(tidyverse)
library(dplyr)
library(ggplot2)
library(plotly)
library(lubridate)
library(mco)
library(FRAPO)
library(scatterplot3d)
library(akima)
library(fields)
library(PerformanceAnalytics)
library(fPortfolio) ## para donlp2NLP
library(cccp)
library(fpp3)
library(BatchGetSymbols)
library(PortfolioAnalytics)
library(ROI)
require(ROI.plugin.glpk)
require(ROI.plugin.quadprog)
library(PerformanceAnalytics)
library(quadprog)
library(KraljicMatrix)
library(doParallel)
registerDoParallel()
Intro
Neste post trabalharemos na perspectiva da problemática de Seleção de Portfólio, considerando os seguintes tópicos:
Como na maioria dos casos, a limitação pela definição de objetivos de múltiplos critérios (conflitantes) com relação a problemas de otimização de portfólio;
O conceito de Eficiência de Pareto (soluções não-dominadas)
Soluções/pontos podem ser determinados com algos do tipo NSGAII (Genéticos ou Evolucionários) e Multicriteria Decision Making (MCDM)
Aplicações para um portfolio com diferentes ativos com os seguintes macro-objetivos:
Retornos médios;
Covariância de risco total
Diversificação com relação a contribuições individuais de risco de cada ativo
Otimização Multicritério (problema)
\[\begin{align} \min \quad f_m (\omega), & \quad m = 1, 2,\cdots,M; \\ s.a. \quad g_j(\omega)\geq 0, & \quad j = 1, 2, \cdots, J; \\ h_k(\omega) = 0, & \quad k = 1, 2, \cdots, K; \\ \omega_i^{(L)} \leq \omega_i \leq \omega_i^{(U)}, & \quad i = 1, 2, \cdots, n \end{align}\]
Ou seja, temos um problema de \(M\) funções-objetivos (conflitantes) e \(n\) variáveis (restritas).
Então a solução \(\widehat{\omega} \in \Omega\) será eficiente (Pareto Ótima ou não-dominada ) se não existir \(\omega \in \Omega\) tal que \(f_k (\omega) \leq f_k (\widehat{\omega})\,|\, k = 1, \cdots,p\) e se \(f_i(\omega) < f_i (\widehat{\omega})\) para qualquer \(i \in \{ 1, \cdots, k \}\)
Otimização Multicritério (Eficiência de Pareto)
Objetivo: encontrar soluções que estejam na frente e contemplem todo o alcance da eficiência de Pareto.
Vale ressaltar que o algoritmo NSGAII não necessariamente encontrará os pontos ótimos, ou seja, muito próximos a fronteira.
Esse algoritmo passa pelas seguintes etapas:
cria população aleatória,
seleção/escolha (não dominante/restrição dominante),
aplicação de variação (crossover, mutação),
elitismo (aglomeração de distâncias).
Otimização Multicritério (método da soma ponderada)
\[\begin{align} \min \quad \displaystyle \sum_{m=1}^{M}\lambda_m f_m (\omega), & \quad \mbox{com} \,\,\lambda_m \geq 0; \\ s.a. \quad g_j (\omega) \geq 0, & \quad j = 1, 2, \cdots, J;\\ h_k(\omega) = 0, & \quad k = 1,2,\cdots,K;\\ \omega_{i}^{(L)} \geq \omega_i \geq \omega_i^{(U}, & \quad i=1,2,\cdots, n \end{align}\]
Aqui a escala ou normalização nas funções-objetivo é importante, sendo que os objetivos e/ou níveis de satisfação podem ser incluídos.
Possibilidade de uma abordagem híbrida, onde alguns objetivos são especificados como \(\epsilon\)-restritos.
Artigos e trabalhos de reprodução
Cálculo de superfície não dominada em problemas de três critérios: Hirschberger et al. (2013).
Formulação do problema EMO bi-critério com descontinuidades no espaço de busca (risco e retorno com (i) alocações zero ou dentro dos limites e (ii) restrição de cardinalidade na contagem dos ativos incluídos): Deb et al. (2011).
Problemas de três critérios (quad-lin-lin):
Risco, retorno e custos de transação: Steuer et al. (2005), Steuer et al. (2013).
Risco, retorno e índice ESG: Utz et al. (2015).
Exemplo de aplicação portfólio \(n-\) ativos
Carga de dados da carteira
portfolio <- BatchGetSymbols(
tickers = c("ZC=F", # Futuros Milho
"ZO=F", # Futuros Aveia
"KE=F", # Futuros KC HRW Wheat Futures
# "ZR=F", # Rough Rice Futures
"GF=F", # Feeder Cattle Futures
"ZS=F", # Futuros oleo de soja
"ZL=F", # Futuros Soja
"ZM=F" # Futuros farelo soja
),
first.date = "2019-01-01",
last.date = Sys.Date(),
do.cache = FALSE)
portfolio <- as.data.frame(portfolio$df.tickers) %>%
select(
ref.date,
ticker,
price.close
) %>%
pivot_wider(
names_from = ticker,
values_from = price.close
)
head(portfolio)glimpse(portfolio)Rows: 1,421
Columns: 8
$ ref.date <date> 2019-01-02, 2019-01-03, 2019-01-04, 2019-01-07, 2019-01-08, 2019-01-09, 2019-01-10, 2019-01-11, 2019-01-14, 2019-01-…
$ `ZC=F` <dbl> 375.75, 379.75, 383.00, 382.25, 380.00, 382.00, 376.25, 378.25, 378.50, 371.25, 374.00, 380.00, 381.75, 379.00, 378.7…
$ `ZO=F` <dbl> 278.25, 278.50, 280.00, 279.50, 282.75, 285.75, 288.75, 294.75, 300.00, 292.50, 295.50, 295.75, 298.75, 297.00, 294.7…
$ `KE=F` <dbl> 492.50, 503.50, 506.00, 503.00, 505.00, 505.50, 498.75, 504.50, 499.00, 495.50, 495.50, 504.00, 506.00, 509.75, 515.0…
$ `GF=F` <dbl> 147.950, 146.525, 144.900, 146.000, 147.625, 146.825, 146.750, 146.125, 144.850, 144.750, 143.775, 141.425, 141.450, …
$ `ZS=F` <dbl> 894.75, 900.25, 909.50, 912.25, 906.25, 911.50, 895.50, 899.25, 890.75, 893.25, 894.50, 907.75, 916.75, 909.25, 915.0…
$ `ZL=F` <dbl> 27.90, 28.18, 28.41, 28.26, 28.18, 28.32, 27.94, 28.17, 28.11, 28.24, 28.23, 28.77, 29.01, 29.06, 29.38, 29.51, 30.03…
$ `ZM=F` <dbl> 311.0, 312.7, 315.1, 318.2, 317.6, 319.0, 312.6, 310.4, 306.9, 309.3, 310.1, 312.2, 315.1, 313.0, 312.9, 312.3, 313.9…Mensalizo o dataset pra pegar o último valor de cada mês (para rodar o script de forma mais rápida)
library(timetk)
portfolio <- xts::xts(portfolio[,-1], order.by = portfolio$ref.date)
monthly_dataset_xts <- do.call(rbind, lapply(split(portfolio, "months"), last))
class(monthly_dataset_xts) [1] "xts" "zoo"monthly_dataset <- as.data.frame(monthly_dataset_xts)
monthly_datasetLembrando que:
ZC=F, \(\Rightarrow\) Futuros MilhoZO=F, \(\Rightarrow\) Futuros AveiaKE=F, \(\Rightarrow\) Futuros KC HRW Wheat FuturesZR=F, \(\Rightarrow\) Rough Rice Futures (não incluído)GF=F, \(\Rightarrow\) Feeder Cattle FuturesZS=F, \(\Rightarrow\) Futuros oleo de sojaZL=F, \(\Rightarrow\) Futuros SojaZM=F\(\Rightarrow\) Futuros farelo soja
Obteremos agora, os valores de partida, considerados benchmarks para o nosso portfólio:
Prices <- timeSeries(monthly_dataset, charvec = rownames(monthly_dataset))
R <- returns(Prices, method = "discrete", percentage = TRUE) %>%
as.data.frame() %>%
mutate(
Date = seq(ymd('2019-02-01'), Sys.Date(), by = 'month')
) %>%
select(
Date, everything()
)
R <- xts::xts(R[,-1], order.by = R$Date)
# Equal weight benchmark
n <- ncol(R)
equal_weights <- rep(1 / n, n)
benchmark_returns <- Return.portfolio(R = R,
weights = equal_weights,
rebalance_on = "years")
colnames(benchmark_returns) <- "benchmark"
# Benchmark performance
table.AnnualizedReturns(benchmark_returns)plot(benchmark_returns)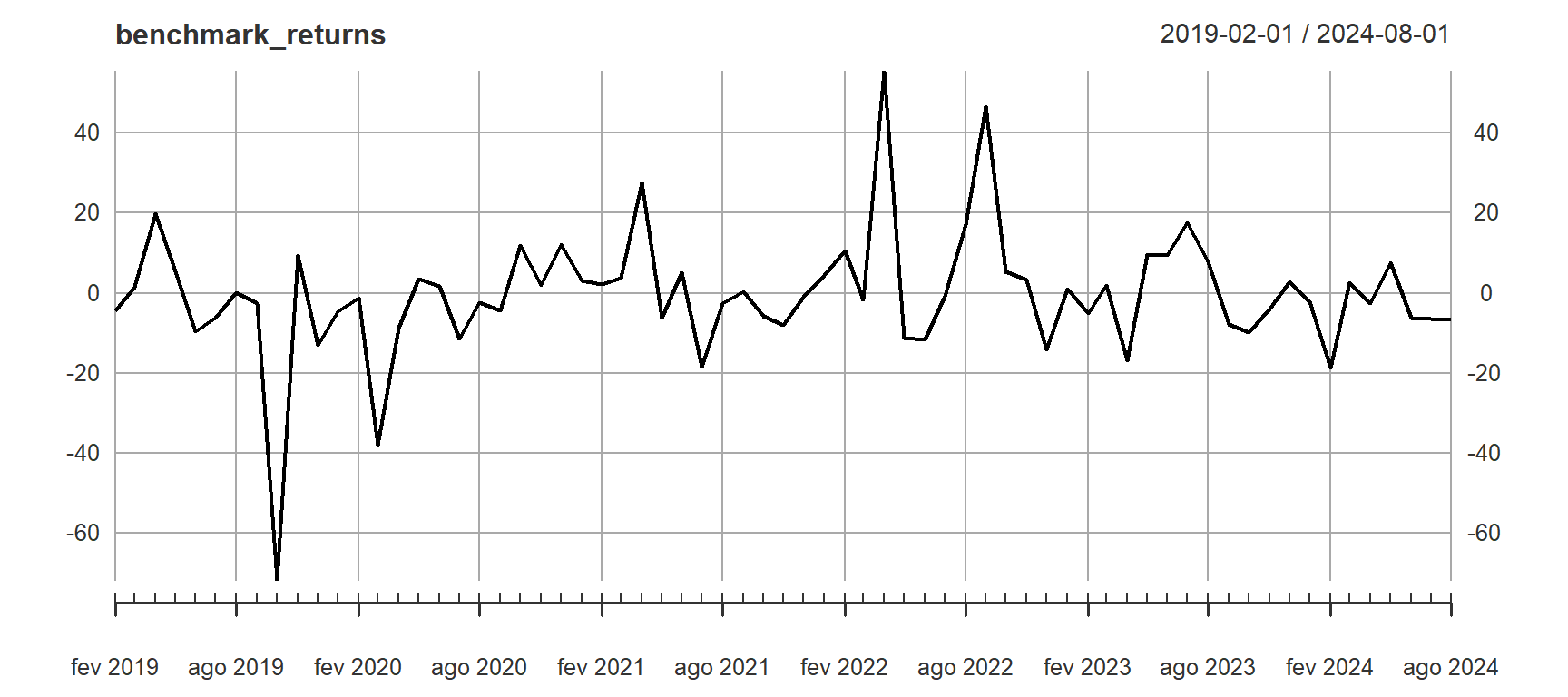
A Otimização Multicritério consistirá em três objetivos:
Retornos médios;
Volatilidade e;
Dispersões das parcelas de risco
Os benchmarks definidos serão pré-estabelecidos como 6% ao ano para os retornos e uma volatilidade esperada anual na ordem dos 4%.
Vamos verificar os padrões temporais de cada ativo no portfólio, iniciando com as séries de preços:
# create function that is used in lapply
plotlines <- function(variables){
ggplot(monthly_dataset, aes(x = seq_along(variables), y = variables)) +
geom_line() + xlab("") + ylab("")
}
# plot all plots with lapply
plots <- lapply(monthly_dataset,
plotlines) # all colums except
plots$`ZC=F`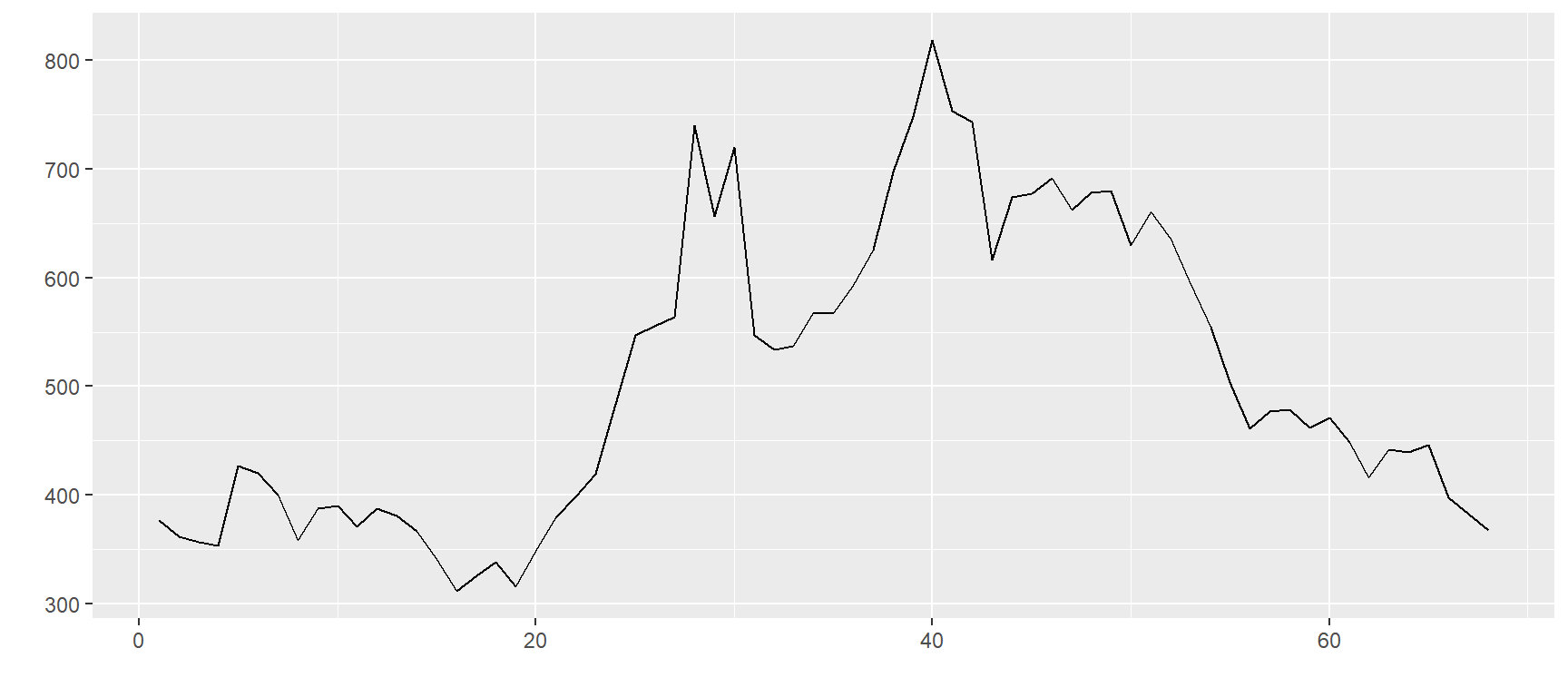
$`ZO=F`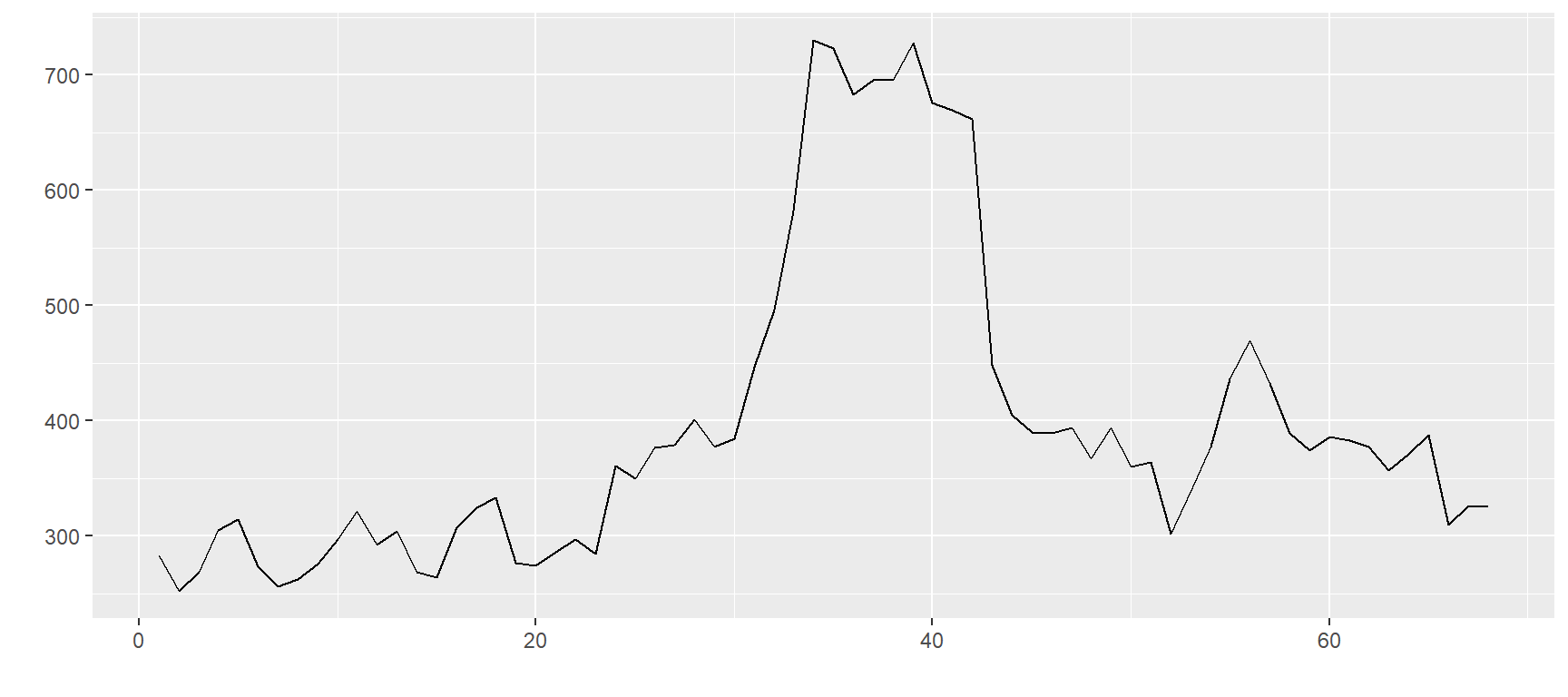
$`KE=F`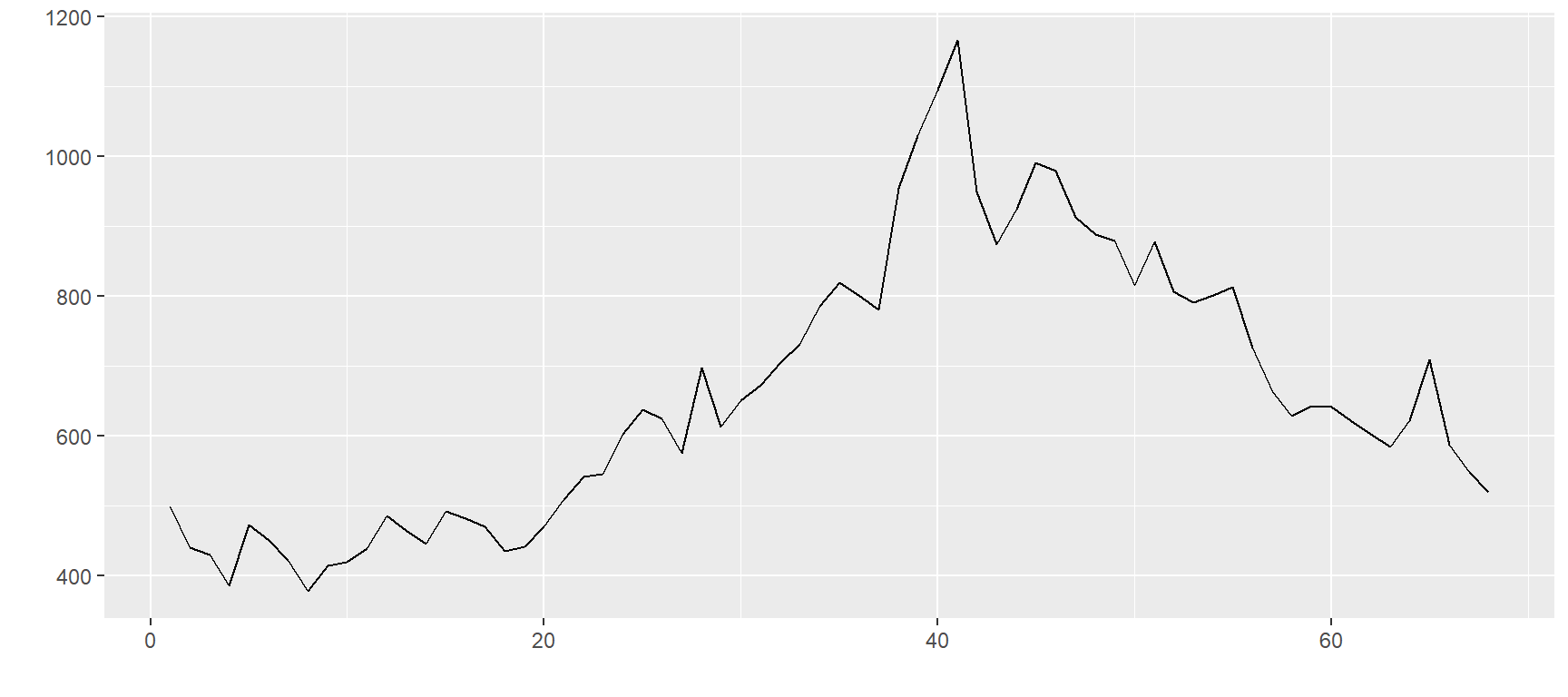
$`GF=F`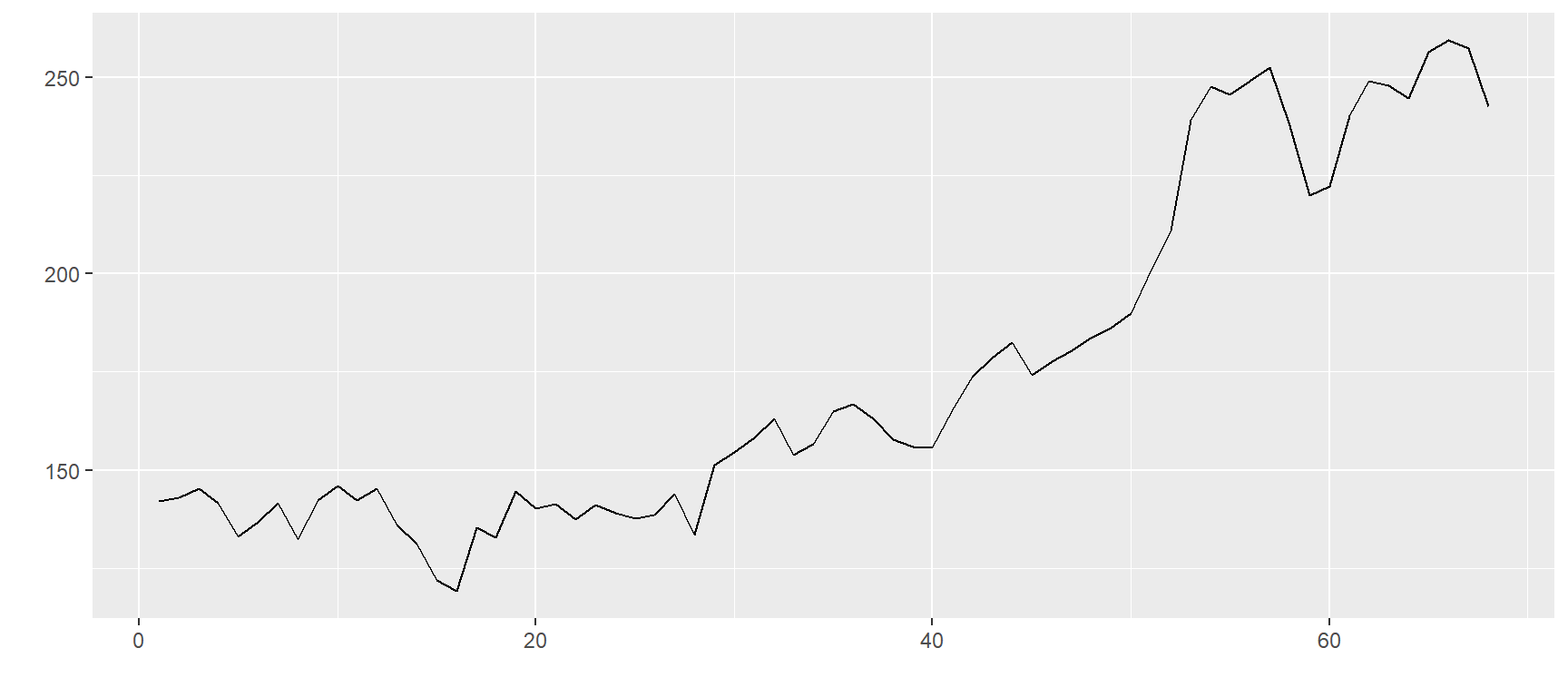
$`ZS=F`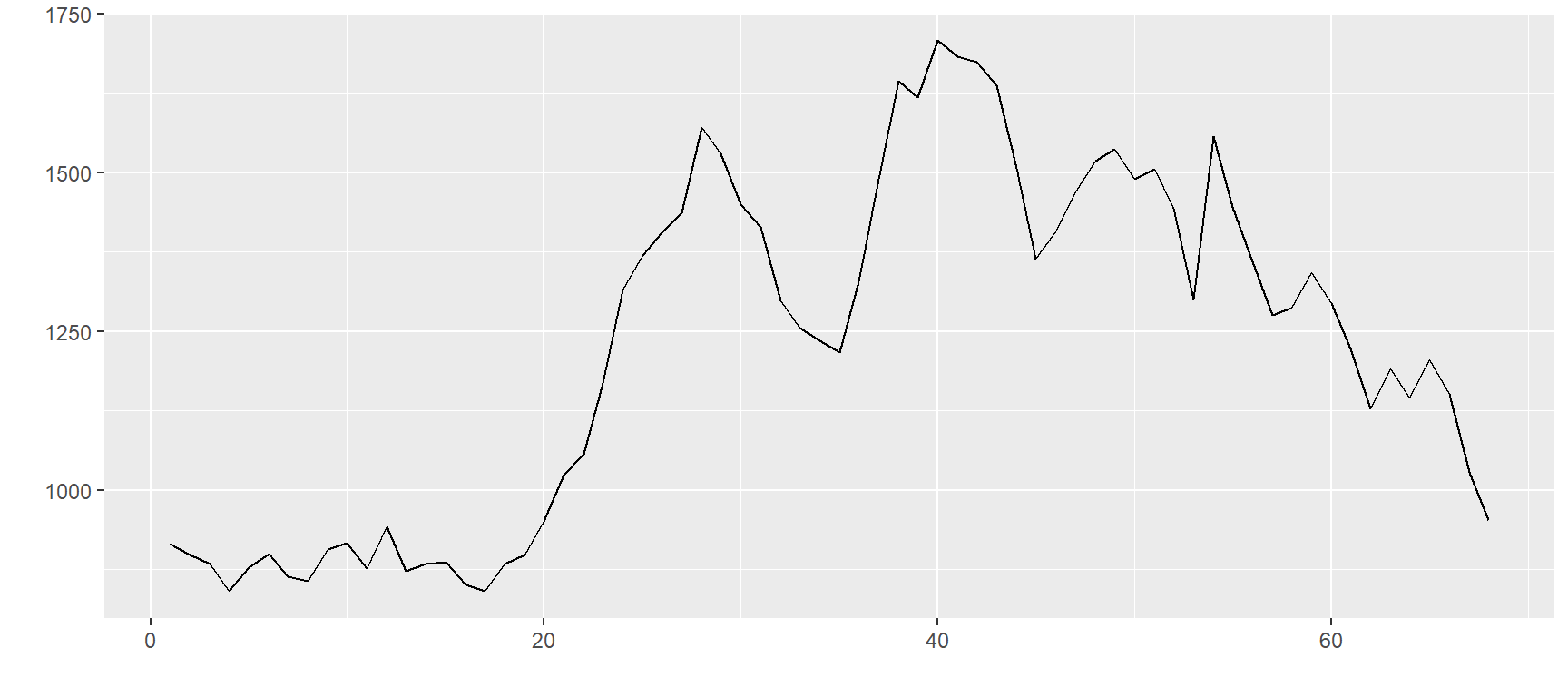
$`ZL=F`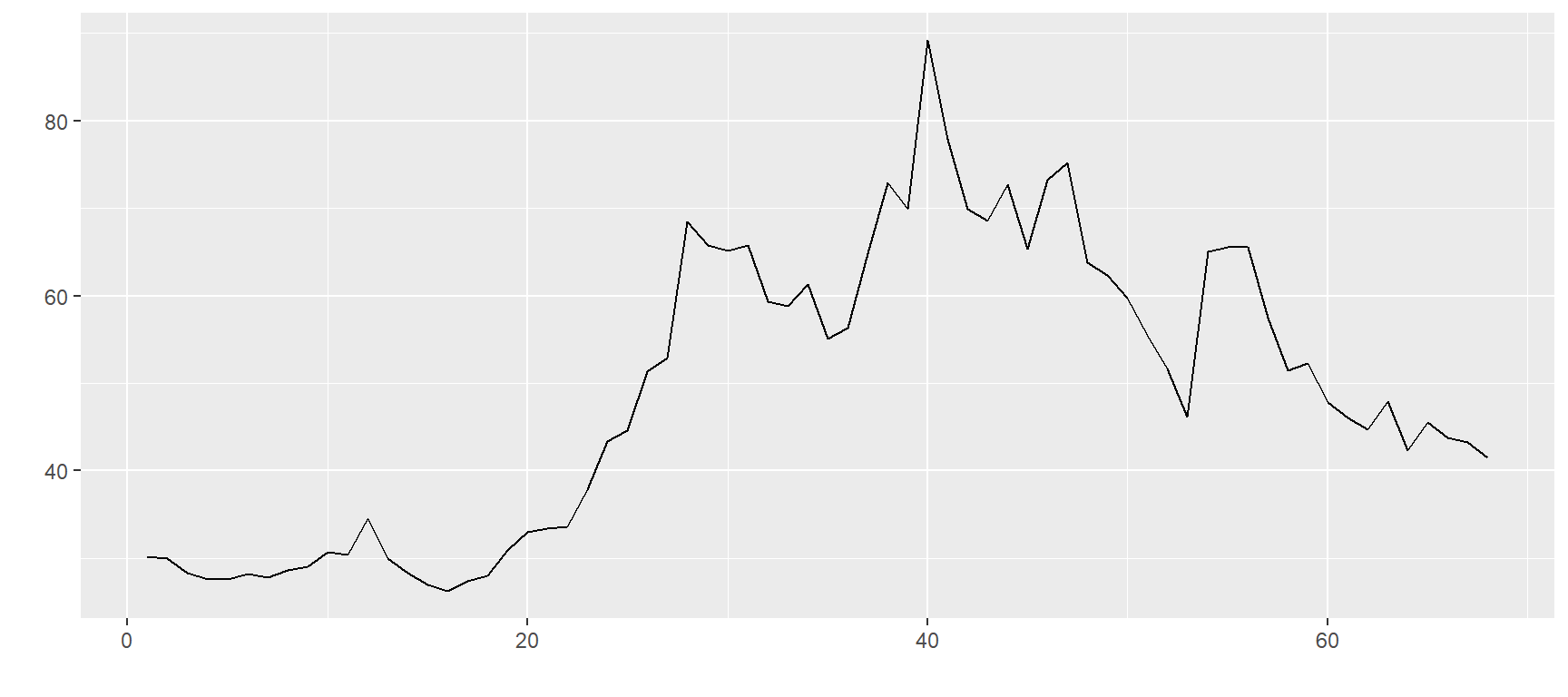
$`ZM=F`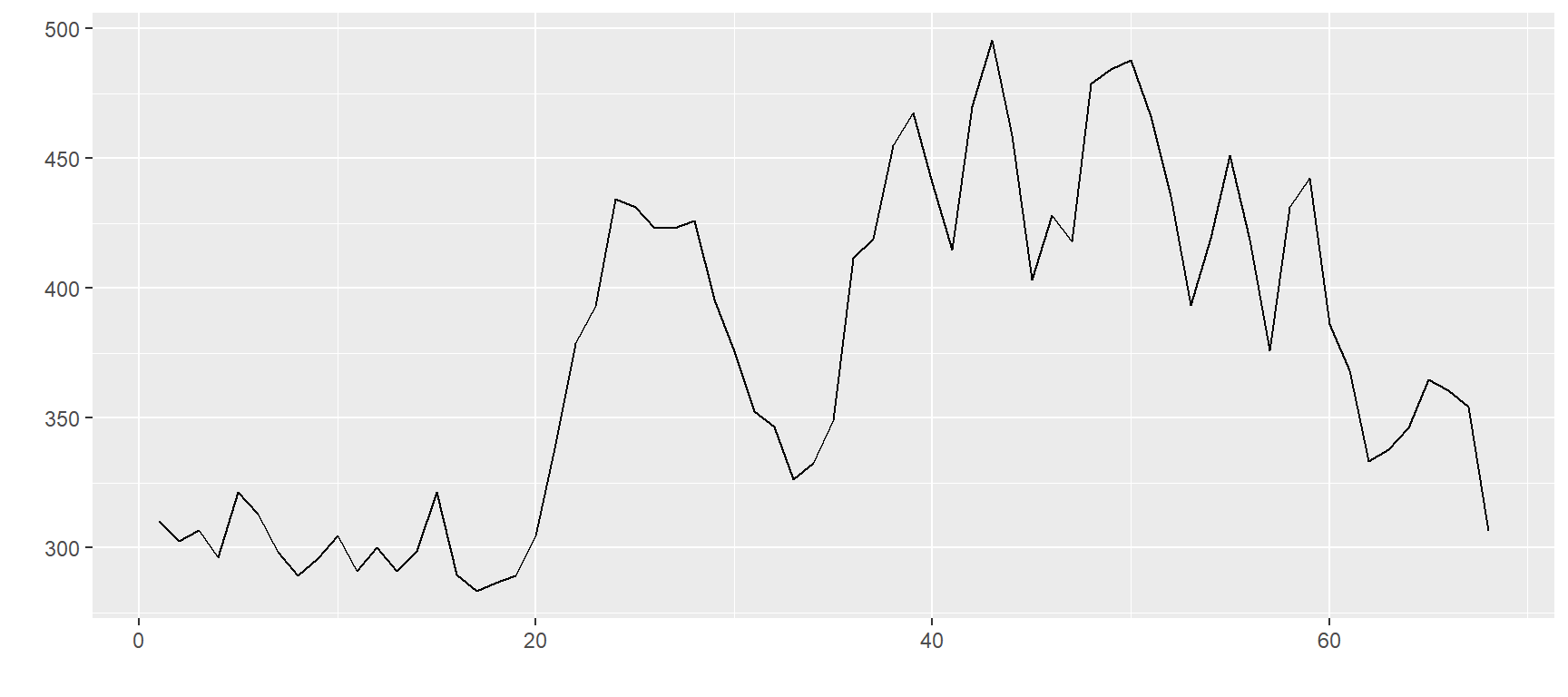
E em seguida pelos padrões de retornos:
Prices <- timeSeries(monthly_dataset, charvec = rownames(monthly_dataset))
R <- returns(Prices, method = "discrete", percentage = TRUE)
# create function that is used in lapply
plotlines <- function(variables){
ggplot(R %>% as.data.frame(), aes(x = seq_along(variables), y = variables)) +
geom_line() + xlab("") + ylab("") +
geom_hline(yintercept = 0, color = "red")
}
# plot all plots with lapply
plots <- lapply(R,
plotlines) # all colums except
plots$`ZC=F`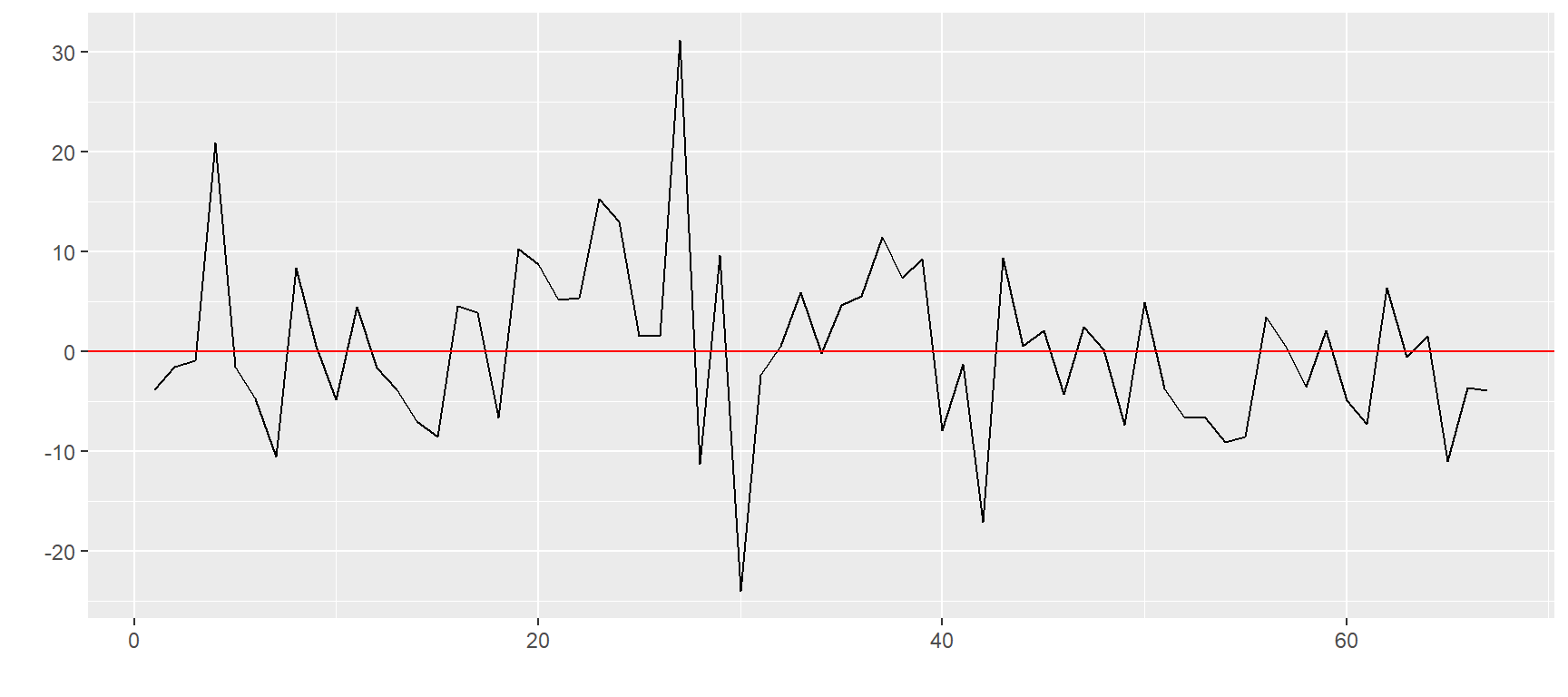
$`ZO=F`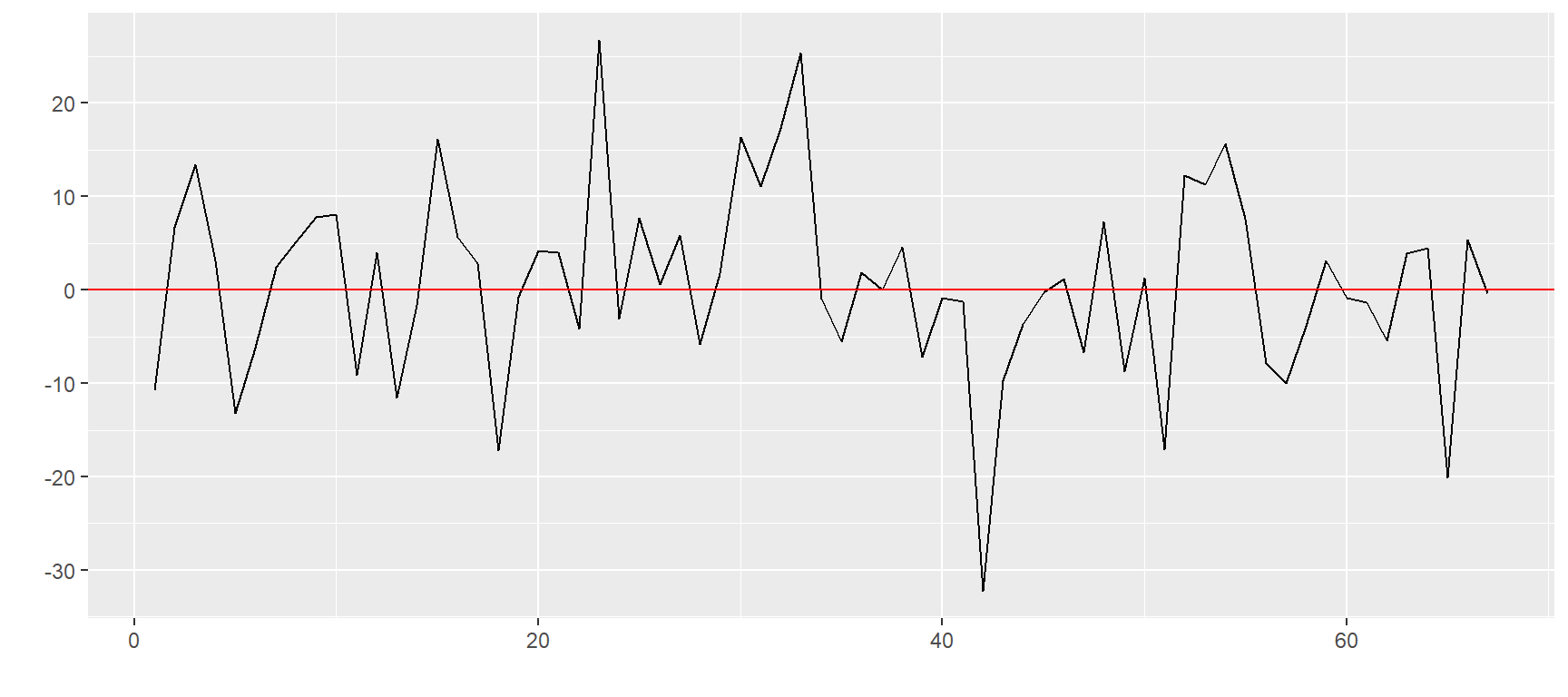
$`KE=F`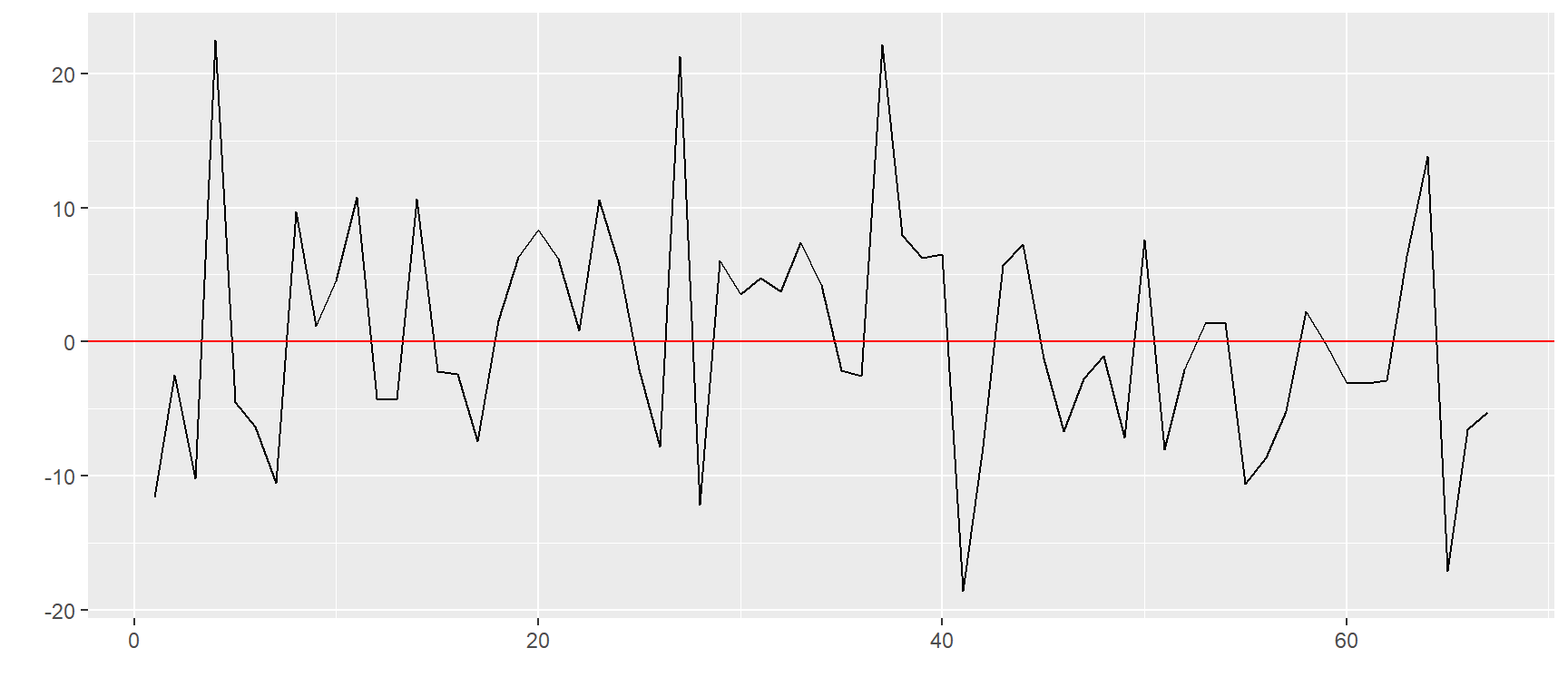
$`GF=F`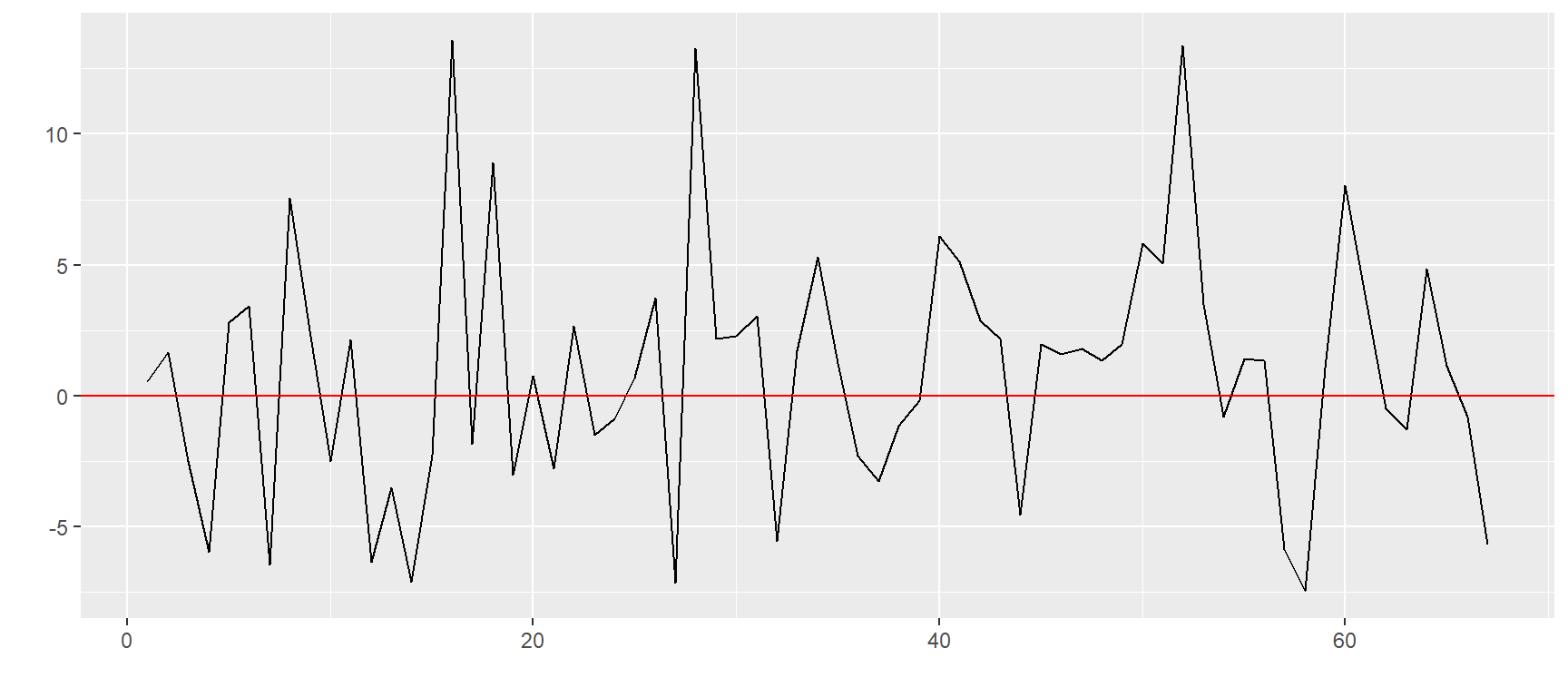
$`ZS=F`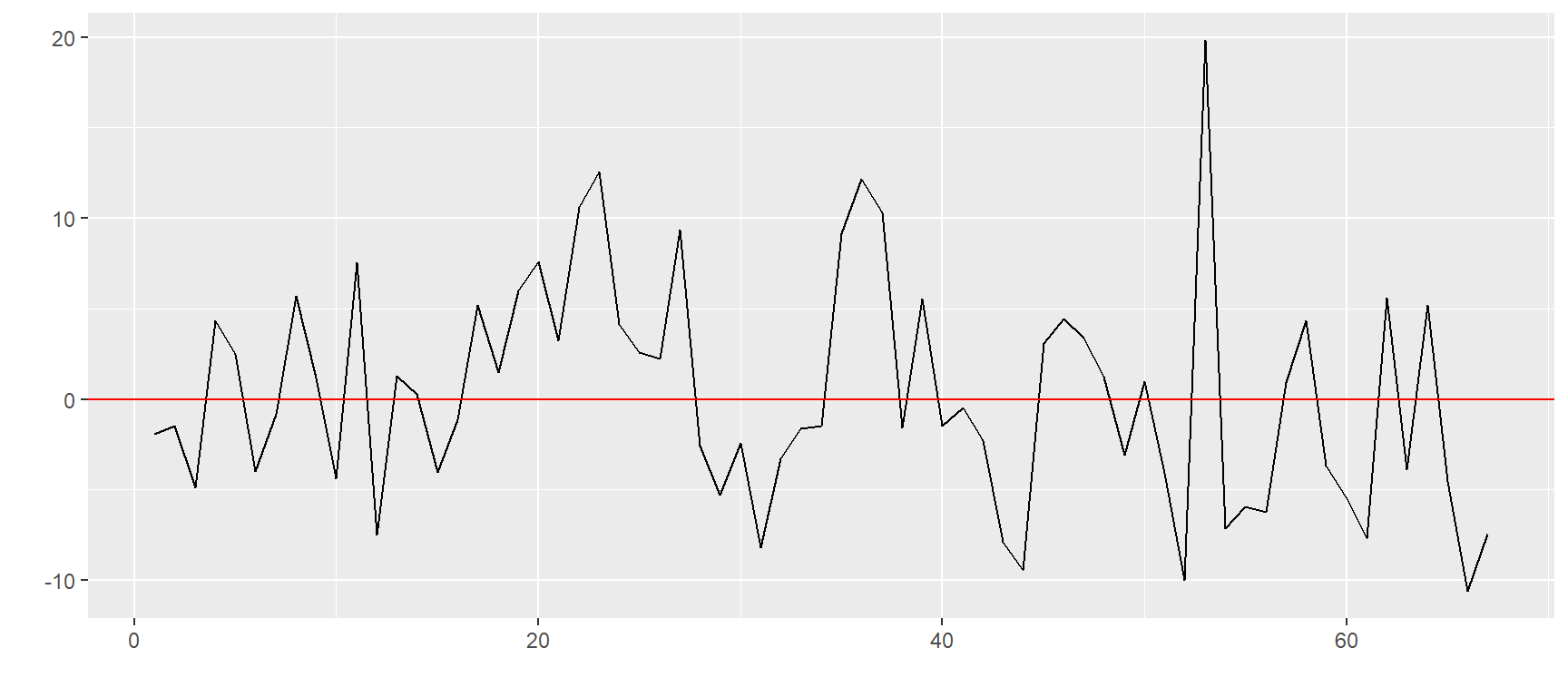
$`ZL=F`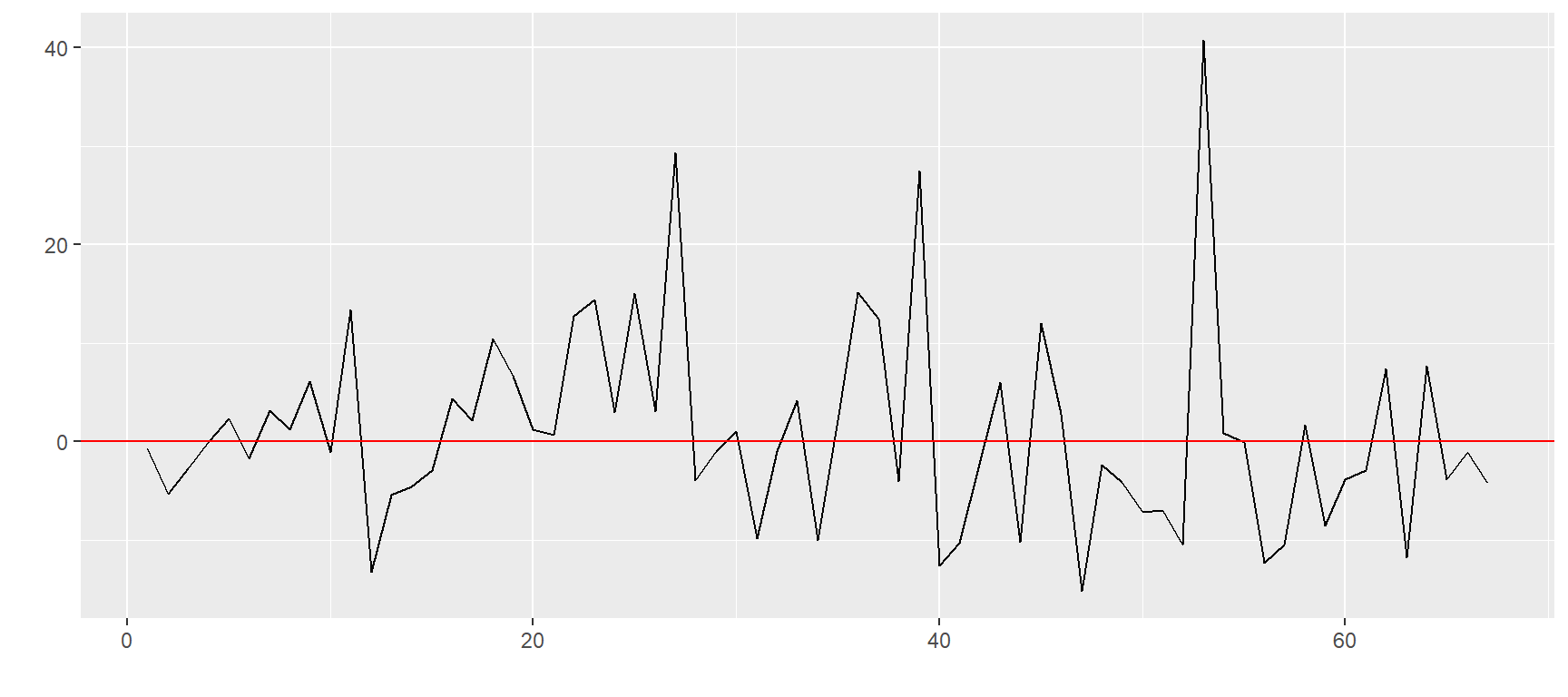
$`ZM=F`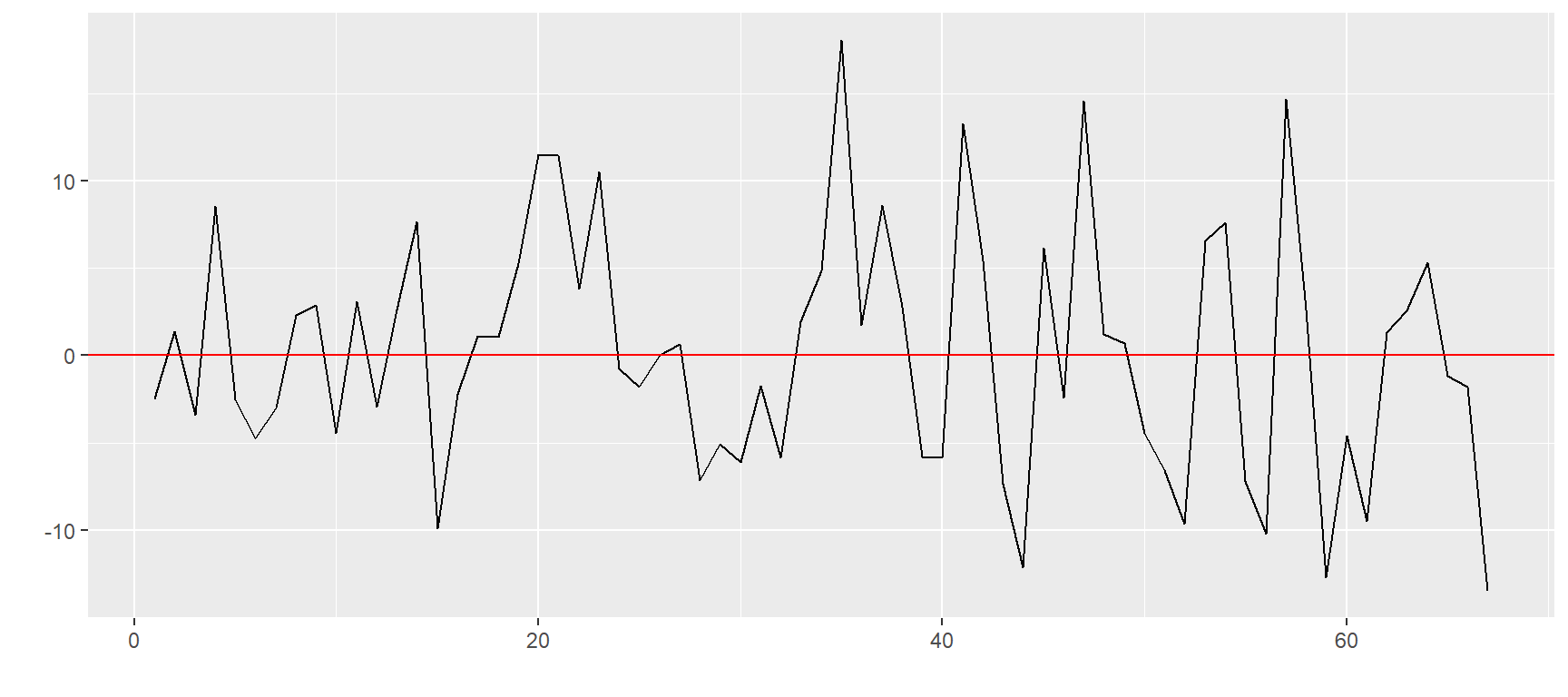
Em seguida definimos os benchmarks (metas ou TMA´s)
NAssets <- ncol(Prices) # Numero de ativos na carteira
## Definindo os parâmetros
TargetRpa <- 6 ## percentagem anual 6%
TargetR <- 100 * ((1 + TargetRpa / 100)^(1 / 12) - 1) # Equiv. taxas pra mes [(1+i)^(q/t)]-1*100
TargetVol <- 4 ## percentual ao ano 4%
l <- rep(1, 3) ## objetivo dos pesos
WeightedSum <- FALSE
mu <- colMeans(R) # Media dos retornos por ativo no portfolio
mu ZC=F ZO=F KE=F GF=F ZS=F ZL=F ZM=F
0.3173787 0.7259347 0.4063655 0.9084737 0.2413093 0.9451097 0.2199165 S <- cov(R) # Ideal covariância negativa
S ZC=F ZO=F KE=F GF=F ZS=F ZL=F ZM=F
ZC=F 72.746469 13.366281 43.212000 -9.999881 24.146655 31.168070 16.769237
ZO=F 13.366281 102.194493 26.278248 -5.191233 1.535882 13.659945 -2.181994
KE=F 43.212000 26.278248 71.151845 -9.181398 18.723994 27.791685 12.960283
GF=F -9.999881 -5.191233 -9.181398 22.217139 -3.334809 -3.595979 -5.307503
ZS=F 24.146655 1.535882 18.723994 -3.334809 37.854423 44.014351 25.650662
ZL=F 31.168070 13.659945 27.791685 -3.595979 44.014351 103.395024 12.784180
ZM=F 16.769237 -2.181994 12.960283 -5.307503 25.650662 12.784180 48.839763Definição das funções objetivo
Objetivos Multicritério e Restrição Orçamentária:
# Definição da função-objetivo
f <- function(x){
y <- numeric(3)
y[1] <- -1.0 * l[1] * drop(crossprod(x, mu)) / TargetR
y[2] <- l[2] * drop(sqrt(t(x) %*% S %*% x)) * sqrt(12) / TargetVol
y[3] <- l[3] * sum((mrc(x, S) / 100)^2)
if(WeightedSum){
return(sum(y))
} else {
return(y)
}
}
g <- function(x){
c(1.01 - sum(x), sum(x) - 0.99)
}Formalmente essa função pode ser representada por
\[\begin{equation} f(x) = \begin{cases} \sum_{i=1}^{3} y_i & \text{if } \text{WeightedSum} \\ y & \text{caso contrário} \end{cases} \end{equation}\] \[\begin{align*} \text{Onde: } y_1 & = -l_1 \frac{x^T\mu}{\text{TargetR}} \\ y_2 & = l_2 \frac{\sqrt{x^TSx}\sqrt{12}}{\text{TargetVol}} \\ y_3 & = l_3 \sum \left(\frac{\text{mrc}(x, S)}{100}\right)^2 \end{align*}\] \[\begin{equation} g(x) = \{1.01 - \sum_{i} x_i, \sum_{i} x_i - 0.99\} \end{equation}\]
Determinação das soluções Pareto Eficientes:
# Roda um algoritmo NSGAII pra otimização
ans <- nsga2(f,
NAssets,
3,
lower.bounds = rep(0, NAssets),
upper.bounds = rep(1, NAssets),
constraints = g,
cdim = 2,
popsize = 500)
names(ans)[1] "par" "value" "pareto.optimal"## Setando os valores dos objetivos para os gráficos
mco <- data.frame(ans$value[ans$pareto.optimal, ])
mcomco[, 1] <- ((1 + (-1.0 * mco[, 1] * TargetR) / 100)^12 - 1.0) * 100
mco[, 2] <- mco[, 2] * TargetVol
colnames(mco) <- c("Retorno", "Risco", "Diversificacao")
head(mco) # Frente de ParetoPlotamos o gráfico em 3 dimensões:
scatterplot3d(mco,
main = "Soluções Pareto Eficientes",
sub = "Frente de Pareto (Superfície)",
xlab = "Objetivo: Retornos",
ylab = "Objetivo: Risco",
zlab = "Dispersão de pesos dos ativos",
angle = 15,
highlight.3d = FALSE,
box = TRUE,
color = "steelblue",
pch = 19, type = "p",
cex.symbols = 0.6)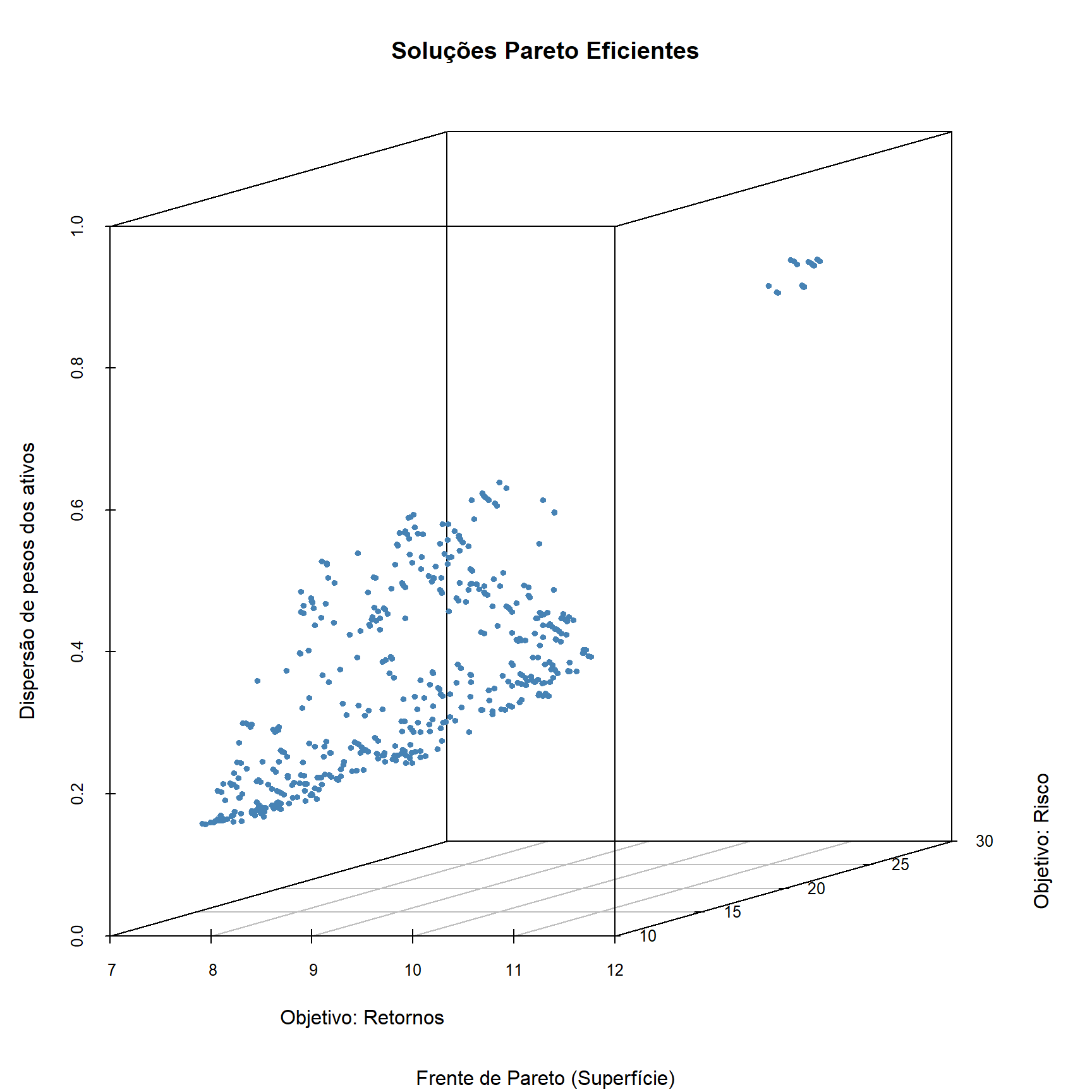
Faremos agora de maneira interativa essa visualização da superfície (frente de Pareto)
p <- plot_ly(data = mco,
z = ~ Retorno,
x = ~ Risco,
y = ~ Diversificacao,
color=~Diversificacao,
colors = c('#0C4B8E' ,'#BF382A'),opacity = 0.5) %>%
add_markers(x = ~ Risco,
y = ~ Diversificacao,
z = ~ Retorno, #No eixo z sempre coloque a variavel dependente
marker = list(size = 5),
hoverinfo = 'text',
text = ~paste(
"Retorno", Retorno, "<br>",
"Diversificacao", Diversificacao, "<br>",
"Risco", Risco))
pPlotamos o gráfico do conjunto eficiente:
s <- interp(mco[, 2], mco[, 1], mco[, 3],
xo = seq(min(mco[, 2]), max(mco[, 2]), length = 100),
yo = seq(min(mco[, 1]), max(mco[, 1]), length = 100),
duplicate = "mean"
)
par(mar = c(5, 6, 5, 6))
image.plot(s, nlevel = 50,
main = "Plot do conjunto eficiente",
legend.lab = "Dispersão dos pesos dos ativos",
xlab = "Objetivo: Risco",
ylab = "Objetivo: Retornos",
legend.mar = 4,
horizontal = TRUE,
legend.shrink = 0.7,
col = topo.colors(50))
contour(s, add = TRUE, nlevels = 20, labcex = 0.8)
points(mco[, 2], mco[, 1], pch = 18, cex = 0.4, col = "orange")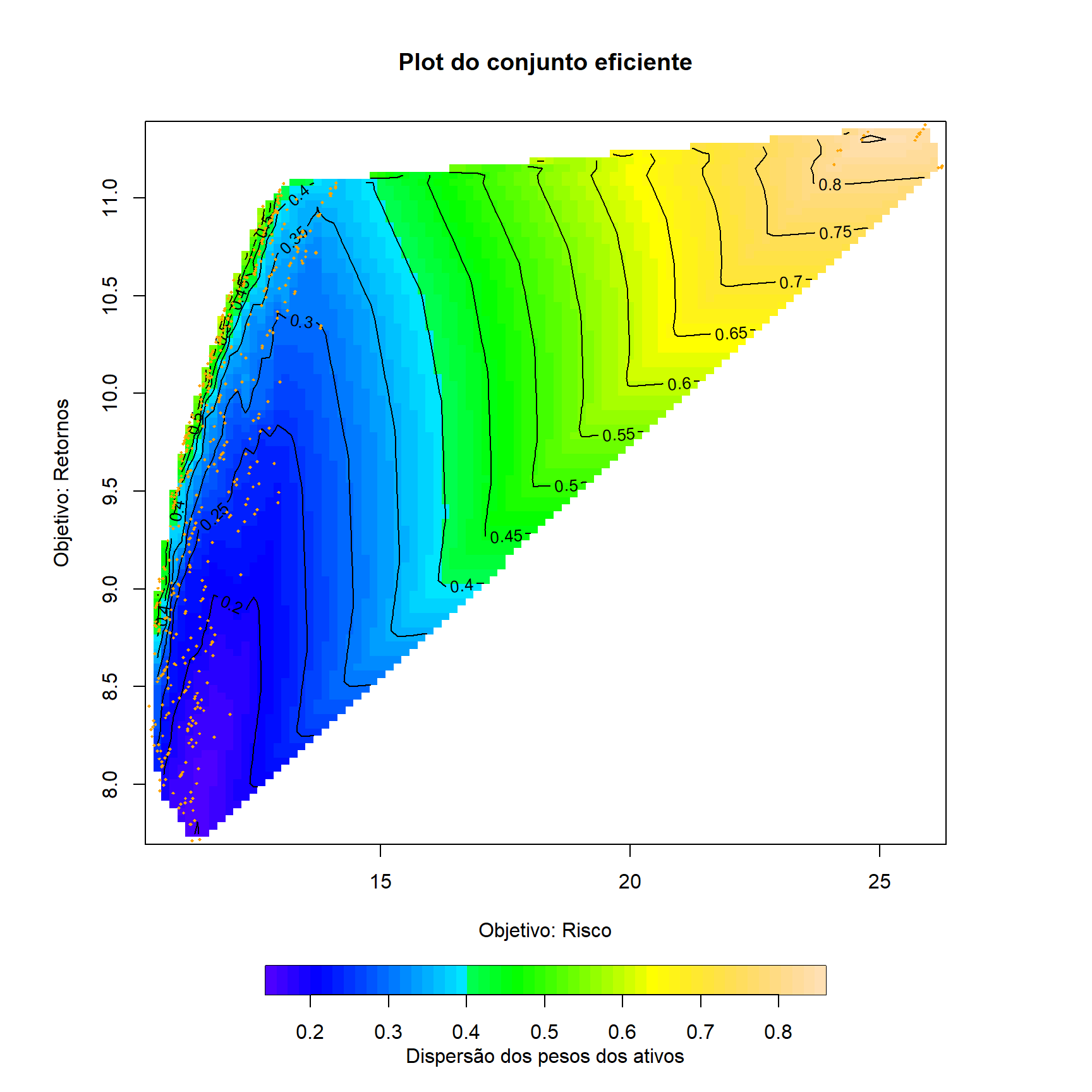
Gero a frente de PAreto com o ggplot
ggplotly(
ggplot(mco, aes(x = Risco, y = Retorno )) +
geom_point() +
theme(axis.text = element_text(size = 7),
axis.title = element_text(size = 7) ) +
theme(plot.title = element_text(size = 7, face = "bold")) +
ggtitle("Frente de Pareto para risco x retorno portfolio de commodities") +
# geom_smooth(span = 0.3) +
geom_frontier()
)
Referências
Deb, K., R. Steuer, R. Tewari, and R. Tewari. On the effectiveness of a nsga-ii local search approach customized for portfolio optimization. KanGAL Report 2011007, Indian Institute of Technology Kanpur, Kanpur, India, 2011.
Steuer, R., Y. Qi, and M. Hirschberger. Multiple objectives in portfolio selection. Journal of Financial Decision Making 1 (1)., jun, 2005.
Steuer, R., M. Wimmer, and M. Hirschberger. Overviewing the transition of Markowitz bi-criterion portfolio selection to tri-criterion portfolio selection. Journal of Business Economics 83(1), 61–85, 2013, fev.
Hirschberger, M., R. Steuer, S. Utz, and M. Wimmer. Computing the nondominated surface in tri-criterion portfolio selection. Operations Research 61(1), 169–183, jan-fev. 2013. Utz, S., M. Wimmer, and R. Steuer. Tri-criterion modeling for constructing more-sustainable mutual funds. European Journal of Operational Research 246(1), 331–338, out., 2015.
R packages
citation(package = "akima")Para citar o pacote 'akima' em publicações use:
Akima H, Gebhardt A (2022). _akima: Interpolation of Irregularly and Regularly Spaced Data_. R package version 0.6-3.4,
<https://CRAN.R-project.org/package=akima>.
Uma entrada BibTeX para usuários(as) de LaTeX é
@Manual{,
title = {akima: Interpolation of Irregularly and Regularly Spaced Data},
author = {Hiroshi Akima and Albrecht Gebhardt},
year = {2022},
note = {R package version 0.6-3.4},
url = {https://CRAN.R-project.org/package=akima},
}citation(package = "cccp")Para citar o pacote 'cccp' em publicações use:
Pfaff B (2023). _cccp: Cone Constrained Convex Problems_. R package version 0.3-1,
<https://CRAN.R-project.org/package=cccp>.
Uma entrada BibTeX para usuários(as) de LaTeX é
@Manual{,
title = {cccp: Cone Constrained Convex Problems},
author = {Bernhard Pfaff},
year = {2023},
note = {R package version 0.3-1},
url = {https://CRAN.R-project.org/package=cccp},
}citation(package = "fields")Please cite fields including its version and DOI as
Douglas Nychka, Reinhard Furrer, John Paige, Stephan Sain (2021). "fields: Tools for spatial data." R package version
16.2, <https://github.com/dnychka/fieldsRPackage>.
Uma entrada BibTeX para usuários(as) de LaTeX é
@Misc{,
title = {fields: Tools for spatial data},
author = {{Douglas Nychka} and {Reinhard Furrer} and {John Paige} and {Stephan Sain}},
note = {R package version 16.2},
organization = {University Corporation for Atmospheric Research},
address = {Boulder, CO, USA},
year = {2021},
url = {https://github.com/dnychka/fieldsRPackage},
}citation(package = "mco")Para citar o pacote 'mco' em publicações use:
Mersmann O (2024). _mco: Multiple Criteria Optimization Algorithms and Related Functions_. R package version 1.17,
<https://CRAN.R-project.org/package=mco>.
Uma entrada BibTeX para usuários(as) de LaTeX é
@Manual{,
title = {mco: Multiple Criteria Optimization Algorithms and Related Functions},
author = {Olaf Mersmann},
year = {2024},
note = {R package version 1.17},
url = {https://CRAN.R-project.org/package=mco},
}citation(package = "fPortfolio")Para citar o pacote 'fPortfolio' em publicações use:
Wuertz D, Setz T, Chalabi Y, Theussl S (2023). _fPortfolio: Rmetrics - Portfolio Selection and Optimization_. R package
version 4023.84, <https://CRAN.R-project.org/package=fPortfolio>.
Uma entrada BibTeX para usuários(as) de LaTeX é
@Manual{,
title = {fPortfolio: Rmetrics - Portfolio Selection and Optimization},
author = {Diethelm Wuertz and Tobias Setz and Yohan Chalabi and Stefan Theussl},
year = {2023},
note = {R package version 4023.84},
url = {https://CRAN.R-project.org/package=fPortfolio},
}citation(package = "PerformanceAnalytics")Para citar o pacote 'PerformanceAnalytics' em publicações use:
Peterson BG, Carl P (2020). _PerformanceAnalytics: Econometric Tools for Performance and Risk Analysis_. R package
version 2.0.4, <https://CRAN.R-project.org/package=PerformanceAnalytics>.
Uma entrada BibTeX para usuários(as) de LaTeX é
@Manual{,
title = {PerformanceAnalytics: Econometric Tools for Performance and Risk Analysis},
author = {Brian G. Peterson and Peter Carl},
year = {2020},
note = {R package version 2.0.4},
url = {https://CRAN.R-project.org/package=PerformanceAnalytics},
}citation(package = "FRAPO")To cite the FRAPO package in publications use:
Pfaff, B. (2016) Financial Risk Modelling and Portfolio Optimisation with R, second edition John Wiley & Sons Ltd,
London.
Uma entrada BibTeX para usuários(as) de LaTeX é
@Book{,
title = {Financial Risk Modelling and Portfolio Optimisation with R},
author = {B. Pfaff},
publisher = {John Wiley & Sons, Ltd},
address = {London},
edition = {2nd},
year = {2016},
url = {http://www.pfaffikus.de},
}
For BibTex versions of citations use: toBibtex(citation('FRAPO'))
Total execution timing:
end_time <- Sys.time()
end_time - start_timeTime difference of 39.15306 secs